ARTÍCULOS
Los fundamentos matemáticos: teoría de las finanzas
Ulises Cárcamo C.*
*Licenciado en Matemáticas de la Universidad de Medellín, Máster en Matemáticas Aplicadas de la Universidad EAFIT, candidato a doctor en Applied and Computational Mathematics (Mathematical Finance), University of Canterbury. Profesor de la Universidad EAFIT.
RESUMEN
Para aquellos estudiosos de las finanzas provenientes de áreas diferentes de la Economía es muy importante el que conozcan las relaciones entre la Teoría Económica de la Elección y las Finanzas. La Teoría de la Elección sirve no solamente de un marco teórico donde inclusive el matemático más formal y estricto puede sentirse a gusto, sino que también, con ciertos ajustes, es una teoría matemática en el sentido estricto.
Este artículo presenta los aspectos básicos de la relación de esta teoría con las finanzas, desde el punto de vista discreto y determinístico. Éste es un primer paso en la conformación de bases teóricas sólidas que permitan no sólo entender las modernas teorías financieras sino también analizar la conveniencia de esas teorías y modelos para explicar los fenómenos financieros de nuestra región.
ABSTRACT
For those approaching Finance from backgrounds different from Economics it is very important to know the relation between Finance and the Economic Theory of Choice. Theory of Choice acts not only as a theoretical frame where even the more strict and formal mathematicians can feel comfortable within, but also (with some adjustments) as a theory in the true mathematical sense. This article, which presents the basic relations between Theory of Choice and Finance, from the discrete-deterministic point of view, is a first step in the construction of solid theoretical foundations that will allow us to understand modern finance literature as well as to analyze the fitness of modern theories and models for our regional financial world.
INTRODUCCIÓN
Día a día vemos cómo aumenta el número de ingenieros, matemáticos, estadísticos y físicos interesados por incursionar en el mundo de las finanzas. La principal motivación parece ser la familiaridad que estos profesionales tiene con algunas de las herramientas que últimamente se están usando en tal área: Transformadas de Fourier, procesos estocásticos, ecuaciones diferenciales estocásticas y elementos finitos, entre otros. Todo esto además de que muchos están bastante acostumbrados a trabajar con métodos numéricos (en general), ecuaciones en diferencia, series de tiempo y métodos econo-métricos básicos.
El problema básico es que aunque se conozcan bien las herramientas, si se desconocen los fundamentos de la teoría en la cual se están aplicando, se pueden cometer errores metodológicos, de interpretación o simplemente, uno se puede complicar la vida en la búsqueda de soluciones.
Por ejemplo, la ecuación diferencial de Black-Scholes se puede transformar en una ecuación de conducción de calor en una dimensión y, por ende, puede aplicársele la teoría de las soluciones de las ecuaciones parabólicas (conocida entre matemáticos, físicos e ingenieros) y después de muchos esfuerzos se llega a una solución general de la que deben eliminarse unas familias de soluciones por carecer de sentido financiero.
El Teorema Fundamental de las Finanzas, por otro lado, establece, bajo la suposición de ausencia de arbitraje, la posibilidad de valorar derivados como los valores esperados de ciertos procesos, usando la medida de probabilidad apropiada. Este último es un resultado muchísimo más general y que demanda menos esfuerzo.
Un resultado intermedio, pero de gran generalidad, se puede deducir aplicando el Teorema de Feynman- Kac a la ecuación original. En ambos casos, la economía de esfuerzos y la facilidad de interpretación y verificación de los resultados del modelo justifican el cambio de metodología.
Por otro lado, el profesional de las matemáticas evita trabajar en "el aire", es decir, necesita de un soporte conceptual, de una teoría, si es posible axiomatizada, en la que pueda sentirse seguro en cuanto a sus deducciones y supuestos y donde, además, pueda analizar los alcances y las limitaciones de sus resultados. La ausencia de cursos como los de Microeconomía o Economía Financiera en su formación profesional dificulta el que pueda vislumbrar la relación entre los fundamentos teóricos y los conocimientos y técnicas básicas, de fácil aplicación, que se encuentran en los textos de Matemáticas Financieras y/o Administración Financiera.
Este artículo es una modesta contribución a "cerrar la brecha" en este segundo aspecto y desde los puntos de vista discreto y determinístico. Está basado principalmente en las ideas de dos importantísimos teóricos de las finanzas: Eugene Fama y Merton Miller quienes presentaron un trabajo en Teoría de las Finanzas, "desde las bases", hace más de tres décadas. En ningún momento se pretende que sea completamente estricto desde el punto de vista matemático. Es más bien una presentación semi-formal y, al mismo tiempo, una invitación a seguir profundizando en las bases a través de las referencias bibliográficas y cualquier otro tipo de material adecuado para tal fin. Mirado desde otro punto de vista, servirá de ejemplo para mostrar cómo los que estudiamos matemáticas, para alcanzar cierto grado de generalidad, tenemos la necesidad de "complicar las cosas".
LA TEORÍA DE LAS FINANZAS
La Teoría de las Finanzas (TF) estudia cómo los individuos y las firmas deben ubicar recursos, a través del tiempo, de manera óptima. En particular, busca explicar cómo la existencia de mercados de capitales facilita la óptima ubicación de tales recursos.
Podemos mirar las conexiones entre la TF y la matemática desde dos puntos de vista: La TF como una teoría matemática per sé, y la TF como una rama de la economía financiera que utiliza muchas de las teorías y herramientas matemáticas más elaboradas de nuestra época. Estos puntos de vista no son excluyentes, más bien se complementan mutuamente. Sin embargo, insistiremos más en el primer punto de vista aunque se mencionarán de paso los conceptos matemáticos que se pueden usar para describir una situación dada.
Como cualquier teoría matemática, la TF está basada en un conjunto de axiomas1 y supuestos. Estos axiomas son los mismos de la Teoría Económica de la Elección2.
Hay un subconjunto de axiomas para condiciones de certeza y otro para condiciones de incertidumbre.
Como suponemos que no todos los lectores están familiarizados con esta teoría, presentamos el sistema axiomático3 a continuación.
Un sistema axiomático para la elección racional
En cualquier sistema de elección existen dos elementos a resaltar. Por un lado están los objetos o situaciones de entre los cuales se escoge: Estos forman el Conjunto de Oportunidades; por otro lado están los gustos o preferencias de quien escoge.
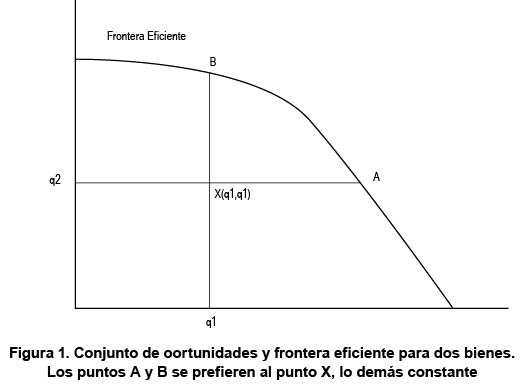
Para caracterizar el primero se establecen las nociones comunes que son las –cajas– o –cestas– de bienes. El conjunto de todas las posibles –cestas– es precisamente el Conjunto de Oportunidades. Este conjunto está limitado por restricciones externas. Estas restricciones son de diversa índole: tecnológicas, legales, del mercado, etc.
Por ejemplo, es imposible conseguir un automóvil que nos lleve de Bogotá a Quito con sólo dos galones de gasolina (limitación tecnológica); legalmente una persona no puede adquirir todos los activos financieros de un país, aunque tuviera el dinero para ello (también es difícil imaginar una situación del mercado en la cual todos los participantes, menos uno, estén dispuestos a vender).
Si se consideraran sólo dos bienes posibles, el conjunto de oportunidades sería un conjunto acotado4 del plano cartesiano, ubicado en el primer cuadrante, dado que las cantidades de cada uno de los bienes son no negativas. Si fueran tres bienes, sería un conjunto acotado del primer octante del espacio tridimensional, y en el caso general de N bienes, un conjunto acotado en el primer octante del espacio N-dimensional5. En este caso cada –cesta– queda completamente especificada estableciendo las cantidades q1, q2,. . ., qN, de cada uno de los bienes, en la n-tupla ordenada (q1, q2, ... , qN). Cuando se quiere distinguir entre n-tuplas se acostumbra agregar un superíndice a cada componente.
La caracterización de la conducta de quien hace la elección, en adelante TD (tomador de decisiones), se hace mediante los llamados Axiomas de la Elección Racional. En este contexto x, y, z representan –cajas–, –cestas– o n-tuplas de bienes de un conjunto de oportunidades pre-deter-minado. Los axiomas utilizan las relaciones primitivas6 de preferencia e indiferencia, haciendo referencia a las –cestas–.
Axioma 1. (Comparabilidad o Completitud)
Dadas dos cestas cualesquiera x e y, el T.D está en uno y solo uno de los siguientes casos:
1. Prefiere x a y (en símbolos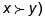
2. Prefiere y a x (en símbolos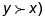
3. Le es indiferente escoger entre x e y (en símbolos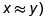
Esto significa que no hay ningún par de –cestas–, en el conjunto de oportunidades, que esté fuera del poder de decisión del TD y además, que este no se contradice: ocurre uno y solo uno de esos casos–.
Axioma 2. (Transitividad de la preferencia y la indiferencia)
Dadas tres cestas cualesquiera x, y, z, se tiene que:
A. Si el TD prefiere x a y, y también prefiere y a z, entonces prefiere x a z.
B. Si al TD le es indiferente escoger entre x e y, y además le es indiferenteescoger entre y y z, entonces le es in-diferente escoger entre x y z.
Nota:
- Una relación compuesta.
Cuando se quiere indicar que "la cesta x es por lo menos –tan buena– como la cesta y" se escribe x >y. Esta relación satisface también completitud y transitividad.
- Axiomas adicionales
Algunos autores agregan las siguientes propiedades entre los axiomas:
• Para toda cesta x, se tiene que x ≈ x (reflexividad)
• Para todo par de cestas x e y, si x ≈y entonces.
Aunque aparentemente estas propiedades son "evidentes", el resaltarlas ayuda a vislumbrar que la indiferencia es una relación de equivalencia. Las relaciones de equivalencia son unos de los ingredientes más importantes de las teorías matemáticas7.
Cuando una preferencia satisface completitud y transitividad se dice que es racional.
Funciones de utilidad para representar relaciones de preferencia.
Cuando una relación de preferencia "≥" es racional, se puede representar mediante una función de utilidad, es decir, una función u definida en el conjunto de oportunidades y con valores reales, que satisface x ≥y si y solo si u(x) ≥ u(y). Además, x ≈ y, si y solo si, u(x) = u(y).
Una relación de preferencia racional dada, se puede representar por muchas funciones de utilidad, es decir, la representación no es única. Sin embargo, todas esas funciones tienen algo en común: preservan las preferencias.
Por ejemplo, las funciones definidas en el conjunto de oportunidades de la figura 1 mediante
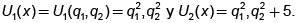Fácilmente se puede comprobar que si x = (q1, q2), y = (q3, q4), entonces x ≥y, si y solo si, U,(x)3 U,(y). y U2(x) > U2(y).
Los puntos x del conjunto de oportunidad tales que su utilidad es igual se llaman conjuntos de indiferencia o iso-utilidad; en el caso bidimensional se llaman curvas de indiferencia (o curvas de iso-utilidad).
Axioma 3. (No saciedad)
El TD preferirá, (o al menos no será indiferente entre estas dos opciones) tener más de un bien cualquiera a tener menos de ese bien, si al mismo tiempo las cantidades que puede tener de otros bienes no disminuyen8.
Este supuesto hace que se descarte la mayoría de los puntos del conjunto de oportunidades y se concentre la búsqueda en la parte de su frontera que "está en la dirección de crecimiento de las curvas de indiferencia". A este conjunto se le llama frontera eficiente.
Después de entender este axioma, tiene sentido la expresión que se utiliza en Teoría de la elección: "Al tomar una decisión racional, el TD se comporta como si estuviera buscando el máximo de una función de utilidad".9
Axioma 4. (Convexidad)
Si x e y son dos cestas tales que U(x) = U(y) y si z es una combinación de estas cestas, de la forma z = α.x + (1–α), y, con 0 ≤ a ≤ 1, entonces U(z) ≥ U(x) =U(y)10.
Convexidad del conjunto de oportunidades y de las curvas de indiferencia.
Para que el axioma de convexidad sea efectivo, el conjunto de oportunidades (y su frontera) debe ser convexo. ¿Puede el lector atento encontrar qué tipo de problemas se pueden presentar si lo anterior no se cumple?
La misma propiedad la deben cumplir los conjuntos de indiferencia. En el caso especifico de curvas de indiferencia, estas deben ser la gráfica de una función convexa.11
Desde el punto de vista geométrico, una función es convexa si, dados dos puntos cualesquiera de su gráfica el segmento de recta que los contiene está por encima de la gráfica. Una definición más analítica: f es convexa12 si para dos puntos cualesquiera de su dominio x1 y x2 y todo 0 ≤ a ≤ 1, se cumple que f(α.x1 + (1– α).x2) ≤ α.f(x1) + (1–α) f(x2).
Una consecuencia del axioma de no saciedad
Una consecuencia directa de este axioma es que las curvas de indiferencia de una función de utilidad de dos variables crecen en la dirección de cada uno de los ejes coordenados y, por ende, también crecen en sentido diagonal. Esto limita bastante las funciones matemáticas que pueden fungir como una función de utilidad.
La elección racional bajo las restricciones del conjunto de oportunidades
Recordemos que al tomar una decisión racional, el T.D., se comporta como si estuviera buscando el máximo de una función de utilidad. Esto se verá reflejado en un recorrido del conjunto de oportunidades en la dirección en la que aumenta la utilidad.
Como el conjunto es acotado, debe encontrarse un punto en el que una de las curvas de nivel intercepte uno de los puntos de la frontera, y cualquier intento de aumentar la utilidad llevaría hacia fuera del conjunto (hacia una región de imposibilidad, dadas las restricciones); es decir se ha alcanzado la máxima utilidad posible, dentro de las restricciones impuestas13.
Aplicaciones de la teoría de la elección a las finanzas
Antes de hacer alguna aplicación a las finanzas se debe hacer un cambio metodológico: En vez de cestas de bienes como elementos fundamentales entre los cuales se elige, se consideran los llamados "consumos totales14 en el tiempo t", o "estándares de vida en el tiempo t", Ct=p1tq1t+ p2tq2t + ... + pntqnt, donde los pit, son los precios de los bienes (o servicios) consumidos en el instante t y los qit, son las respectivas cantidades consumidas.
En este momento se deben hacer dos clasificaciones: Tiempo discreto o tiempo continuo, y ambientes de certeza o riesgo.
Es mucho más simple comenzar con tiempo discreto y ambiente de certeza. Es decir, el tiempo transcurre no continuamente sino "a saltos" y suponemos conocida la información básica en esos instantes de tiempo.
De ahora en adelante supondremos que el tiempo está compuesto por instantes t = 0, t = 1, ... y que tanto los precios como las cantidades a consumir son conocidos con certeza en cada instante del tiempo.
El TD tiene ahora que elegir entre n-tuplas de consumos, en los instantes de tiempo pre-determinados. Esta elección estará representada por la función de utilidad U(C1, C2,..., Cn) en un modelo de n-períodos.
No es muy difícil demostrar que esta elección, representada por la nueva función de utilidad para los consumos, cumple las mismas propiedades de la elección en términos de las cestas de bienes15.
Mercados de capitales
Uno de los elementos más importantes del sistema financiero son los mercados de capitales.
Son estos los que permiten que los individuos consuman de manera eficiente a través del tiempo, dado que propician que los individuos o las empresas consigan dinero prestado o faciliten la labor de prestar dinero. Sin mercados de capitales establecidos un individuo con superávit de dinero hoy, pero con escasas posibilidades de ingresos adicionales en el futuro se vería abocado a prestar dinero a muy bajo interés. Por otro lado, es muy probable que individuos con escasos recursos en la actualidad pero con prometedoras oportunidades en el futuro, se vieran forzados a pagar altísimos intereses para poder financiar sus proyectos actuales.
Como veremos, el mercado facilita una sola tasa de interés que refleja el equilibrio y que beneficia a ambas partes: a los facilitadores de dinero y a quienes requieren el dinero. Además, los individuos ajustarán sus necesidades de prestar o pedir prestado de tal manera que lo hagan de la manera óptima con respecto a la tasa de interés del mercado.
En este punto, los planes de consumo son eficientes en el sentido en que nadie puede mejorar su situación sin que otro empeore la suya. Los economistas llaman a este tipo de eficiencia, Eficiencia de Pareto o Eficiencia Paretiana16.
Así como el mercado evita que se desperdicien muchas oportunidades de inversión por falta de fondos, también evita que se desperdicien a causa de ignorar que existen. Los individuos no tienen que recorrer muchos lugares en busca de tales oportunidades; en las bolsas y en los sitios especializados pueden encontrar toda la información requerida. Esto conduce a que las inversiones se hagan también de una manera eficiente.
Un ente tan complejo como el mercado de capitales no se puede representar fácilmente; así que para incluir sus efectos en la teoría de las finanzas se necesita una representación idealizada de él.
Mercados perfectos y recursos
Un constructo teórico de especial importancia es el mercado perfecto de capitales donde se pueden comprar y vender todos los bienes y servicios para los "consumos" o "estándares de vida".
Estos mercados son los que satisfacen:
1. Todos los participantes del mercado gozan de iguales oportunidades de acceso a la información acerca de los precios establecidos y otras características importantes de los bienes o servicios transadosx. Esta información es gratuita.
2. Las acciones comerciales de los compradores, los vendedores y los emisores de bienes no afectan los precios del mercado.
3. No hay costos de transacción ni impuestos para compra, venta o emisión de bienes.
Como los participantes del mercado están igualmente informados y su comportamiento es racional, se descartan las oportunidades de arbitraje. Es decir, no es posible comprar en un sitio, vender en otro (prácticamente al mismo tiempo) y obtener un beneficio basado en la diferencia de precios.
Creemos que el lector está suficientemente familiarizado con modelos matemáticos como para comprender las diferencias entre este mercado y los mercados reales, así como la utilidad y limitaciones de estos modelos.
Una consecuencia importante
La unicidad de precios es una consecuencia importante de suponer un mercado de capitales perfecto. Dado que todos los participantes están bien informados y todos satisfacen el axioma de no saciedad, ninguno estará dispuesto a vender al precio más bajo y a comprar al más alto. Esto paralizaría las transacciones del bien con dos precios, hasta que un solo precio esté establecido.
El conjunto de oportunidades para los mercados de capitales perfectos
Lo que realmente se compra y se vende en los mercados de capitales son sumas de dinero que van a ser entregadas en varios instantes del tiempo.
Si s y t son dos instantes del tiempo y s < t, denotemos con sPt el valor que hay que pagar en el instante s por una unidad monetaria que va a ser entregada en el instante t. Diremos en este caso que se compra un derecho18 a recibir la cantidad de dinero. También podemos decir que compra un contrato con ese derecho.
Ejemplo 1. Supongamos que alguien deposita $1–000.000 en una cuenta de ahorros con un interés simple del 12% anual y al cabo del año retira el capital más los intereses. Esto se puede representar diciendo que el depositario está comprando $1–120.000, en este momento, y que esa cantidad le será entregada dentro de un año. El costo de ese dinero es 0P1 = 0.892857142 (pesos hoy por un peso dentro de un año).
El modelo de dos períodos
Este modelo, aunque es bastante simple, contiene los elementos fundamentales de modelos más complejos.
Consideremos dos períodos, 1 y 2 de tal manera que se tienen dos ingresos y1 y y2, dos consumos c1 y c2 y el neto, a2, de activos financieros adquiridos en el período 1 y que maduran en el período 2 y/o posibles deudas (de signo negativo) contraídas en el primer período y que deben ser canceladas en el segundo período.
Así, c2= y2 + a2. Esta es una restricción sobre el conjunto de oportunidades. Por supuesto, la cantidad que el TD puede consumir en el segundo período depende del consumo en el primer período. Si en éste sus recursos son y1 + a1, entonces
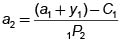y por lo tanto
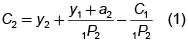
Este resultado tiene una interpretación geométrica: la última expresión es una recta en el plano C1C2 que es la frontera eficiente del conjunto de oportunidades. Como el conjunto debe cumplir con esta restricción (1), este se colapsa en esa recta.
El máximo consumo en el segundo período, 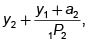se encuentra cuando el TD se abstiene de consumir en el primer período e invierte todos sus recursos. Por otro lado, si quiere hacer todo su consumo en el período 1, a expensas de sus futuros ingresos, podrá hacerlo hasta por la cantidad y1 + a1 + y2.1p2.
Este último es el valor del mercado de sus ingresos actuales y futuros.
Un caso intermedio se da cuando consume en cada período ingresos correspondientes y corresponde al punto (y1 +a1, y2).
Es importante notar que la pendiente de la recta que determina la frontera eficiente es .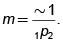
El punto de vista de las tasas de interés
Si P es la cantidad de dinero q se posee en el primer período y F es la cantidad que se puede comprar para entrega al comienzo del segundo período al precio 1p2, entonces 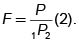Si
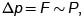entonces
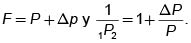La cantidad
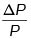es la tasa de crecimiento de la suma invertida durante el primer período. Se la suele representar mediante 1r2 y se llama –tasa de interés de un período–, la expresión
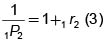se conoce comúnmente como –factor de acumulación, en un período, a la tasa 1r2–. De las expresiones (2) y (3) se puede deducir
que F= P.(1 + 1r2) y de acá que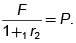
Esta suma, P, es precisamente el valor presente de F unidades monetarias, entregadas en al comienzo del segundo período, cuando se tiene la tasa de interés 1r2.
Un resultado importante
De la expresiones (1) y (3) se puede deducir
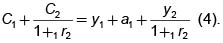
Esta última se puede expresar de la siguiente manera: las combinaciones eficientes de consumos o estándares de vida en los dos períodos, de entre los que el TD debe escoger son aquellas cuyo valor presente del consumo total iguala el valor presente del total de los recursos.
Ejemplo 2. En el ejemplo 1, F= 1–120.000, P= 1–.000.000, ΔP = 0.12 y el factor de acumulación de un período a la tasa de interés de 0.12 es 1.12.
Unicidad de la tasa de interés
Como es de esperar, en un mercado perfecto (no solamente en el de este modelo), existe una sola tasa de interés. Esto es una consecuencia directa de la unicidad de precios.
La distribución óptima de recursos
Como en el caso general, la distribución óptima de recursos se logra en el punto de tangencia de la curva de indiferencia –más alta posible– con la frontera eficiente. Por supuesto, ésta depende de la naturaleza de la función de utilidad y esta última de las preferencias particulares del TD.
En el ejemplo de la figura 6, los consumos óptimos son Cl* y C2*, asociados con el punto A. La misma figura muestra dos puntos no óptimos sobre una misma curva de indiferencia: B y C.
En el punto B, el TD se enfrenta a una situación en la que tiene más que suficientes recursos en el primer período, pero escasos recursos en el período 2. Para alcanzar el punto óptimo, reduce su consumo en el primer período en la cantidad b1~C1*, presta esta diferencia a la tasa de interés 1r2 y en el segundo período con esta diferencia y los intereses logra el consumo C2*. En palabras más acordes con nuestro modelo, –con b1~C1*, compra un derecho a recibir C2*~d2 unidades monetarias en el segundo período–.
En el punto C, el TD se enfrenta a una situación contraria: tiene pocos recursos en el primer período, pero unos más prometedores recursos en el segundo período. En este caso alcanza el óptimo consiguiendo prestado en el primer período, comprometiendo sus futuros recursos en una cantidad d1~C2*. En palabras más acordes a nuestro modelo, –emite un derecho en el cual se compromete a pagar d1 ~ C2* unidades monetarias el segundo período, el valor del derecho es C1 * ~ b2".
Esto significa que el valor presente de C2*~d2 es b1 ~ C1* y que el valor presente de d1~C2* es C1*~b2. Es decir,
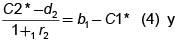
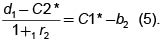
De estas dos expresiones se puede deducir: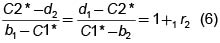
De la geometría de la figura 6 se pueden deducir las relaciones anteriores19 así como también que la pendiente de la frontera eficiente es m = –(1 + 1r2).
El modelo de n períodos
Aunque el modelo de un solo período es suficiente par ilustrar la naturaleza del problema de distribución de recursos, la mayoría de las situaciones del mundo real involucran más de un período.
Ahora, a medida que aumenta el número de períodos aumenta la complejidad del problema.
Pensemos en el caso de cuatro períodos, digamos un plan de a un año, donde se reciben ingresos y existen oportunidades de inversión por cuatrimestres. Necesitamos hablar de cuatro consumos C1, C2, C3 y C4 y por lo tanto la función de utilidad no se puede representar geométricamente. Lo mismo ocurre con el conjunto de oportunidades en general.
Estas, sin embargo no son complicaciones graves. Las verdaderas complicaciones aparecen en las opciones de inversión. Al principio de período se debe decidir si se elige una inversión por 4, 3, 2 ó 1 períodos. Si se elige una inversión por un solo período al final de este hay que decidir si reinvertir a 3, 2 ó 1 período y así sucesivamente.
Ahora, también cabe la posibilidad de dividir los ingresos iniciales en partidas para inversiones por 4, 3, 2 ó 1 período y algo similar cada que se recibe un ingreso. Si el problema consistiera en buscar el máximo beneficio producido por los intereses y si se conocieran todas las tasas de interés involucradas, entonces la Programación Lineal nos ayudaría a resolver este problema.
El meollo del asunto está en cómo establecer unas tasas de interés entre períodos de tal manera que sea imposible el arbitraje.
Para ilustrar este problema y el teorema que lo resuelve, miremos el siguiente ejemplo que demuestra que el precio por unidad monetaria pagada hoy para entregar dentro de dos períodos debe ser igual al producto del precio de una unidad monetaria pagada hoy para ser entregada en el siguiente período y el precio de una unidad monetaria pagada en el segundo período, para ser entregada a comienzos del tercer período.
Ejemplo 3
Este es un ejemplo fácilmente generalizare a una prueba de que 1P3 = 1P2.2P3
Este, aunque muy particular, muestra la filosofía de la prueba para el caso de tres períodos y para el caso general. Suponemos que en el mercado siempre es posible hacer las emisiones que se enuncian a continuación, y que cada una estas tiene demanda.
A. Supongamos que 1P3 >1P2.2P3 . Para ser más concretos, asumamos 1P3= 0.73, 1P2 = 0.8 y 2P3= 0.85. Juan puede emitir un derecho que promete pagar $10.000 al comienzo del tercer período y con el precio $7.300. Inmediatamente recibe este dinero lo invierte en un derecho del primero al segundo período. Por este recibirá 7300/0.8 = $9.125 al comienzo de esta segunda parte, e inmediatamente adquiere un derecho del segundo a tercer período por el que recibirá 9125/ 0.85=$10.735,30. Con esta cantidad puede pagar su obligación y le quedan $735.30 (por cada contrato) como producto de arbitraje.
B. Supongamos ahora que 1P3= 0.62, de tan manera que 1P3< 1P2.2P3, entonces Juan puede comprar uno de estos contratos, que en el caso de la entrega de $10.000 costará $6.200. Ahora, para financiar su proyecto de inversión, Juan emite un contrato que promete pagar 6200/0.8= $7.750 al comienzo del segundo período, con un precio de $6.200. Justo antes de madurar este contrato el emite otro que promete pagar 7.750/0.85 = $9.117,65, con un costo de $7.750. Al madurar este último contrato y el contrato inicial, él recibe $ 10.000, paga $9.117,65 y quedan $882,35 como producto arbitraje por cada contrato de este tipo.
Así que la única manera de evitar el arbitraje es que se cumpla 1P3= 1P2.2P3.
Enunciamos ahora el teorema para n períodos:
Precio libre de arbitraje de un derecho a n-períodos
Teorema
Si tPt+n es el precio de una unidad monetaria comprada en el período t para ser entregada en n períodos después y t+iPt+i+1 es el precio de una unidad monetaria comprada en el período t+i para ser entregada un período después, para i = 0, 1, ... , n-1, entonces tPt+n = tPt+1.t+1Pt+2, ... , .t+n-1Pt+n (7) es el precio libre de arbitraje.
Esbozo de la prueba
A. Supongamos que tPt+n>tPt+1.t+1Pt+2 ... t+n-1Pt+n, + δ, δ > 0. Y que Juan es un hábil participante de este mercado perfecto.
Entonces Juan emite un derecho por una unidad monetaria para ser entregada a comienzos del período n, con un valor de tPt+n.Esta cantidad la invierte inmediatamente en un contrato a un período y a comienzos del siguiente período tendrá 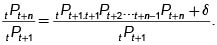Al recibir esta cantidad, la invierte inmediatamente en un contrato por un príodo, de tal manera que termina con
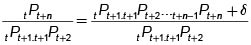que se reinvierten, inmediatamente a un período. Continuando este proceso de invertir por un período y reinvertir inmediatamente; al finalizar los n períodos tendrá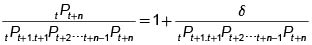
Es decir, Juan podrá cancelar su deuda de una unidad y habrá ganado 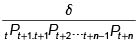con esta estrategia de arbitraje.
B. Supongamos que tPt+n < tPt+1.t+1Pt+2 ... t+n-1Pt+n, entonces tPt+n = tPt+1. t+1Pt+2 ... t+n-1Pt+n, ~ δ, δ > 0. Juan puede adquirir un contrato por una unidad monetaria para ser entregada a comienzos del período n, con un valor de tPt+n.
Este contrato se financiará con la siguiente estrategia: Juan emite un contrato, con un precio de tPt+n, en el que promete pagar , al comienzo del período n. Con el valor recibido paga por su derecho a la unidad monetaria en el período n. Justamente al comenzar el segundo período emite otro contrato, de un período, por el precio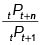
en el que promete pagar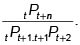
Con la cantidad que recibe paga su obligación en el primer contrato. A comienzos del tercer período emite un contrato de un período, por el precio 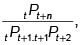prometiendo pagar
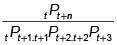a comienzos del próximo período. Con la cantidad que recibe cancela su obligación del segundo contrato. Continuando sucesivamente con el mismo proceso, comienzos del n-simo el recibirá $ 1 del contrato que compro y cancelará lo que adeuda del último que ha emitido, a saber
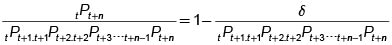
De esta manera se obtiene 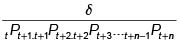. Así se otiene como fruto de esta otra estrategia de arbitraje.
Dado que ambos casos lelvan a arbitraje, la única forma posible, libre de arbitraje es que tPt+n = tPt+1.t+1Pt+2 ... t+n-1Pt+n.
Replicación de contratos a n-períodos
Una consecuencia inmediata del teorema anterior es que cualquier contrato a n-períodos se puede replicar por medio de una serie de contratos a un período20. La consecuencia práctica más importante es la siguiente:
El valor del mercado de un contrato con múltiples entregas
Supongamos un contrato que se paga hoy, tiempo t, y que estipula la entrega de Xt+1, unidades monetarias al final del período 1, Xt+2 unidades al final del período 2,..., Xt+n unidades monetarias al final del período n. Entonces, el valor del mercado de este complejo contrato, en el tiempo t, está dado por:
V(t)=tPt+1.Xt+1+ tPt+2Xt+2+...+tPt+nXt+n = tPt+1.Xt+1+ tPt+1.t+1Pt+2.t+2+...+ Pt+1.t+1Pt+2.t+2Pt+3...t+.n-1Pt+nXt+n. (8)
Ahora 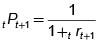y por lo tanto la expresión (8) se transforma en
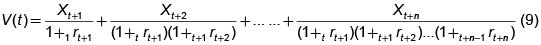
Esta es precisamente la fórmula de valor presente para una sucesión de flujos de caja en diversos instantes del tiempo. Por supuesto, si la tasa de interés es constante, r, durante los períodos considerados se obtiene la famosa fórmula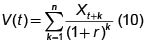
Tasas multiperíodo
La expresión (3) muestra una relación uno a uno entre el precio de una unidad monetaria que se entregará dentro de un período y la tasa de interés para el mismo período. Podemos preguntarnos ¿Existirá una tasa equivalente para el precio de una unidad monetaria que se entregará dentro de n períodos? La respuesta es afirmativa. Ahora, para efectos de comparabilidad con las tasas de un período, esta tasa de n-períodos, 1rn+1 debe ser constante de tal manera que el efecto de las tasas de interés existentes durante los n períodos sea igual al efecto repetido, n veces, de esta nueva tasa. Así, para una cantidad cualquiera, dada, A, debe cumplirse que
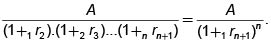
De esta expresión obtenemos
La –estructura por lapsos– o –estructura por períodos– de las tasas de interés21
La sucesión 1r2, 1r3, 1r4, ..., 1rn+1 constitu-ye lo que se llama la estructura por lapsos de las tasas de interés.
En la práctica, el término se aplica a la relación entre bonos (o clases de bienes financieros con el mismo riesgo) con diferentes períodos de maduración y el interés anual que estos ganan durante el tiempo comprendido entre su emisión y su madurez. El análisis de esta estructura requiere de la noción de "riesgo" ausente en este modelo determinístico.
El conjunto de oportunidades del modelo de n-períodos
La caracterización de este conjunto para el caso general se puede obtener mediante un análisis del último período y razonamiento hacia atrás.
En el último período el consumo está dado por Cn = Yn + an y es no negativo. Ahora an se puede representar mediante an = (Yn-1 + an-1 - Cn-1)(1+n-1rn)
Y por lo tanto
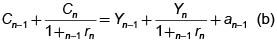
A su vez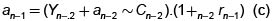
y por lo tanto
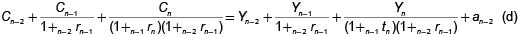
Continuando el proceso llegamos a
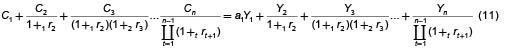
Esta relación tiene el mismo significado que la encontrada en el caso de dos períodos y es independiente de la estrategia o de las estrategias de inversión que se hayan utilizado durante todos los períodos en virtud de la posibilidad de descomposición de un contrato de varios períodos en una serie de contratos de un período.
La interpretación geométrica de esta relación es un hiperplano de n dimensiones en el espacio de los consumos C1 X C2X ... XCn.
Naturalmente, en el caso de tres períodos tendremos un plano que podemos determinar por sus tres cortes con los ejes coordenados. Estas intersecciones corresponden a las situaciones en las que se consume todo en un solo período a expensas de los posibles consumos en los demás períodos.
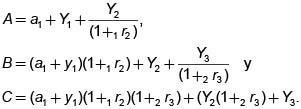
Conjunto de Oportunidades en el Caso de Tres Periodos22
Las rectas AB, AC y BC están relacionadas con solo dos consumos (se sacrifica el consumo de un período invirtiendo la cantidad que podría estar destinada a ello). Las pendientes de estas rectas están dadas por m1 = – (1 + 1r2), m2 = ~(1 + 1r2) (1 + 2r3) y m3 = ~ (1 + 2r3), respectivamente.
En el caso n-dimensional la intersección del hiperplano (11) con el plano CjCk, (j < k para claridad de exposición) es una recta cuya pendiente es
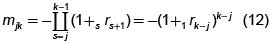
La solución al problema de la distribución de recursos (caso general)
Volvamos al problema original de la maximización de la utilidad U(C1, C2,.. .,Cn), que ahora supondremos diferenciable en una región abierta del espacio n-dimensional que contiene al conjunto de oportunidades. Considerando la restricción (11), la función lagrangiana (o el lagrangiano) correspondiente es
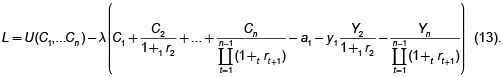
Derivando parcialmente con respecto a cada C, y con respecto a 1 se obtienen las ecuaciones 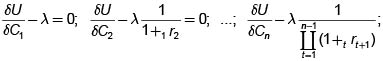(11).
Estas constituyen las condiciones de primer orden para el máximo, que también se pueden escribir como
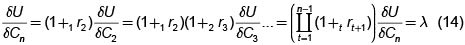y que en virtud de (10) se puede escribir como
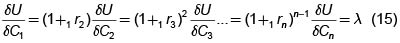
Del cálculo de varias variables sabemos que 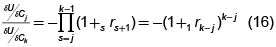es la pendiente de la tangente a la curva de indiferencia U(Cj, Ck)= U0 en el plano CjCk. Comparando este resultado con (12) podemos concluir el la máxima utilidad se encuentra en el punto de tangencia de la intersección del hiperplano (11) con el plano CjCk y la curva de indiferencia, como en el caso de dos consumos. Esto es verdadero para cada par de consumos elegidos.
Mirando al mundo real
Como con todos los modelos, y teorías, fueron necesarios hacer ciertos supuestos que no necesariamente se dan en la realidad. Si estos se cumplieran ya todo estaría resuelto en esta rama del conocimiento y solo habría que mirar las tablas o ejecutar programas de computador y, además, los estudiosos y practicantes de las finanzas serían historia.
Los hechos demuestran lo contrario, día a día vemos cómo nuevas teorías, modelos y herramientas se aplican a las finanzas tratando de obtener resultados lo más parecido posible a los observados.
Así que hagamos un rápido análisis de los supuestos:
En Finanzas el tiempo realmente transcurre a saltos, pero no es posible conocer de antemano elementos importantes como las futuras tasas de interés. Esto introduce el elemento incertidumbre (e inevitablemente el elemento riesgo) y la única manera de reducirla es mediante estimaciones de esos valores inciertos. Los métodos de estimación requieren, naturalmente, algunos supuestos adicionales.
En los mercados reales, aunque hay facilidad de información, esta no es completamente gratuita. Además, las transacciones tienen un costo y hay que pagar ciertos impuestos.
Todavía existen ciertos mercados, no suficientemente equipados con tecnología moderna, donde es posible cierto tipo de arbitraje.
La tasa de interés, definida mediante (3) y considerada como fija dentro de la teoría expuesta, en realidad varía. Está sujeta a las leyes de oferta y demanda de recursos dentro del mercado y a otros factores.
Esta tasa, que representa el equilibrio de esos dos factores, se llama tasa real de interés. La tasa verdadera o tasa nominal de interés (o de retorno) incorpora una prima por inflación23 y una prima por riesgo24.
Contratos a mediano y largo plazo implican, usualmente, mayor riesgo y, por tanto, las tasas de interés correspondientes son más altas. Sin embargo, hay períodos donde las tasas presentan comportamiento contrario y períodos donde son aproximadamente iguales.
Estas diferencias entre los supuestos de la teoría y lo que en realidad se cumple no deben alarmarnos. Estos modelos y la teoría son una primera aproximación que nos permite entender las bases para construir modelos más refinados y aproximados.
De la misma manera que la estática, la cinemática, la dinámica, la termodinámica y los conceptos de energía y trabajo forman una base conceptual que ayudará al ingeniero mecánico en el diseño de una máquina eficiente, esta teoría y otras relacionadas ayudarán al estudioso de las finanzas a entender y diseñar nuevas herramientas financieras.
NOTAS:
1 No sobra advertirle al lector que la noción de axioma es la moderna, muy diferente de aquella, bastante obsoleta, de "verdad auto-evidente" que traían ciertos libros.
2 Y en la Teoría de la conducta del consumidor, en muchos textos de economía.
3 En los sistemas axiomáticos encontramos los siguientes elementos: Nociones comunes o elementos primitivos (p.ej. punto, recta y plano en la Geometría Euclidiana), relaciones primitivas entre elementos primitivos (p.ej. noción –entre– para puntos en una recta), axiomas, definiciones, teoremas, corolarios, etc.
4 Es decir, limitado. Las restricciones son las que le dan la forma a la frontera del conjunto.
5 El lector notará la importancia del Álgebra Lineal para este caso.
6 También se conocen como relaciones no definidas entre términos no definidos.
7 Cualquier relación que sea reflexiva, simétrica y transitiva es una relación de equivalencia. Las relaciones de equivalencia definidas en un conjunto lo dividen en clases de equivalencia. Por ejemplo, considere que existen en el mercado 16 tipos de bonos que maduran a los 5 años y considere todos los posibles portafolios construidos con base en esos 16 bonos y cuyo horizonte es, precisamente, de 5 años. La relación "Dar el mismo rendimiento" definida en esta clase de portafolios es una relación de equivalencia. Las clases de equivalencia están definidas por los rendimientos.
8 Ceteris Paribus: Todo lo demás igual
9 Obviamente es en sentido metafórico. No quiere decir que el TD conozca siquiera la noción de utilidad en el sentido utilizado aquí. Por eso subrayamos la expresión "como".
10 Una combinación de la forma z = α.x + (1- α), y, con 0 ≤ α ≤ 1, se llama combinación convexa de x e y. En geometría, un conjunto de puntos A es convexo, si el segmento de recta que une dos puntos cualesquiera B, y B2 de A pertenece al conjunto. Las diferentes nociones de convexidad juegan un papel importantísimo no solo en geometría sino también en diversas ramas más abstractas de la matemática y en optimización.
11 De la propia función de utilidad no se exige que sea convexa porque las funciones de utilidad consideradas acá son solo funciones "ordinales" es decir, son una forma funcional de las nociones de preferencia e indiferencia.
12 En el lenguaje de algunos textos de cálculo se conocen también como funciones cóncavas hacia arriba.
13 El lector familiarizado con la justificación geométrica del método de los multiplicadores indeterminados de Lagrange reconocerá inmediatamente esta situación.
14 Aunque se habla de "consumos", lo utilizamos en una forma tan amplia que uno de tales consumos podría ser el alquiler de un local durante cierto período.
15 El lector inquieto puede hacer una demostración, relativamente sencilla, para dos períodos. Solo debe tener en cuenta que U(C1,C2) es la máxima utilidad en términos de las cantidades de bienes (q11, q21, q21, q22) y con las restricciones c1= p11.q11 + p21q21, c2= p21.q21 + p22q22.Y probar que los axiomas antes mencionados se cumplen con la nueva función".
16 Diferente de la eficiencia con respecto a la información que es a la que se refiere la "Hipótesis de Eficiencia del Mercado".
17 Cuando esto no se cumple para algunos de los participantes, se habla de asimetría en la información.
18 En inglés claim.
19 Se invita al lector disciplinado a que haga las deducciones basado únicamente en la geometría de la figura 6.
20 El lector debería estar en capacidad de justificar el porqué de esto.
21 En inglés, "The Term Structure of Interest Rates"
22 Es muy importante que el lector comprenda el significado de los puntos A, B y C en términos de consumo e inversión.
23 Representada como una estimación de la inflación futura durante la vigencia del contrato.
24 En el mundo ideal al que pertenece el anterior Mercado Perfecto no hay ni inflación ni riesgo.
Referencias
Fama, Eugene F. and Miller, Merton H. The Theory of Finance. Holt, Rinehart and Winston. New York: 1972.
Gitman, Lawrence J. Principies of Managerial Finance. Seventh Edition. Harper Collins College Publishers. NeyYork: 1994.
Mas-Colell, Andreu et Al. Microeconomic Theory. Oxford University Press. New Cork: 1995.
Van Home, James C. Financial Market Rates and Flows. Fourth Edition. Prentice Hall, Englewood Cliffs. New Jersey: 1994.
Varían, Hal R. Microeconomic Analysis. Third Edition. WW Norton & Company. New York: 1992.