ARTÍCULOS

Las ideas básicas de la valoración de opciones a través del modelo binomial

Ulises Cárcamo C.^*

*Licenciado en Matemáticas Universidad de Medellín, Magíster en Matemáticas Universidad Eafit, candidato a doctor, Docente tiempo completo Universidad Eafit.

RESUMEN

Aunque el estudio de los modelos matemáticos utilizados en la valoración de opciones requiere de una buena preparación en procesos estocásticos continuos y ecuaciones diferenciales estocásticas, las ideas fundamentales detrás de esas representaciones se pueden desarrollar a través de una representación más sencilla, discreta, y con unos requerimientos mínimos de distribuciones de probabilidad. Esta situación se realiza a través de modelos que son una representación de la realidad que, como tal, es sólo una aproximación, haciendo abstracción de algunas de las características observadas, que no se consideran importantes, para resaltar otros aspectos que sí se consideran relevantes.

ABSTRACT

Even though the study of mathematical models used in the pricing of financial options requires a good background in continuous stochastic processes and stochastic differential equations, the basic ideas behind these models can be discussed using a simpler discrete representation with minimal requirements from probability distribution theory. In this case, the models are representing reality and as such, they are aproximation, abstracting out some of the observed features which are not so important, to point out other aspects that are cosidered important.

Introducción

(La Idealización del Mercado)

Ante todo es necesario recordar que un modelo es una representación de la realidad y que como tal es solo una aproximación, una idealización de un fenómeno observado, en la que se hace abstracción¹1 de algunas de las características observadas, que no se consideran importantes, para resaltar otros aspectos que sí se consideran relevantes.

En nuestros modelos consideramos un mercado financiero ideal que tiene las siguientes características:

1. El mercado está libre de fricción, es decir, no hay costos de transacción, no hay diferencia entre el precio al que se quiere vender y el precio al que se quiere comprar un activo, no hay márgenes, no hay restricciones sobre posiciones cortas² y no se pagan impuestos.

2. No hay riesgo de incumplimiento: Los participantes del mercado no tienen riesgo en cuanto a que las contrapartes incumplan los contratos que firmaron.

3. El mercado es competitivo. Esto significa que los agentes del mercado pueden comprar o vender la cantidad de activos que deseen sin afectar los precios.

4. Los participantes del mercado prefieren mayor riqueza a menor riqueza.

5. No hay oportunidades de arbitraje.

En los mercados financieros reales, por lo menos uno de los anteriores supuestos deja de cumplirse:

1. Hay fricción: Siempre hay costos detransacción, hay diferencia entre elprecio al que se quiere vender y elprecio al que se quiere comprar unactivo³. Los facilitadores de mercado⁴ hacen sus ganancias a partir deesta diferencia, por lo tanto, en estemercado ideal no hay este tipo deintermediarios. Para poder negociarcierto tipo de activos, futuros porejemplo, se imponen márgenes (ciertas cantidades de dinero que debenmantenerse disponibles a manera derespaldo).

Las posiciones cortas están reglamentadas de tal manera que no se puede vender corta una acción en un mercado con tendencia a la baja. Además siempre se pagan impuestos.

2. En algunos casos hay riesgo de incumplimiento y por esto se crean leyes y se toman medidas especiales para proteger a los participantes del mercado.

3. En determinadas circunstancias, comprar una cantidad muy grande de activos, acciones por ejemplo, induce a aumentar los precios o venderla lleva a la depresión de estos y, en casos extremos, al pánico⁵.

4. Aunque la mayoría de nosotros aceptaríamos el cuarto supuesto sin pensarlo dos veces, muchos piensan que en determinados casos hay más bienestar con menor riqueza pero con mayores valores morales, por poner un solo ejemplo.

5. Se define como arbitraje cualquier estrategia que permita beneficios sin riesgo de pérdida, a partir de una inversión neta nula. Por ejemplo, si podemos prestar cierta cantidad de dinero en el banco para comprar un lote de acciones y luego con la venta de las acciones pagar al banco lo adeudado más los intereses y quedar con un excedente, entonces hemos aplicado una estrategia de arbitraje. La existencia de las oportunidades de arbitraje es una señal de que la economía está en desequilibrio. En este tipo de economía del sector financiero, los poseedores de portafolios están insatisfechos con sus posiciones dentro de cada portafolio y negocian. Estas negociaciones cambian los precios llevándolos hacia un nuevo equilibrio. En este equilibrio, los inversionistas están contentos con ellos y no hay más oportunidades de arbitraje.

Bueno, nos preguntaremos, ¿y un mercado tan ideal sí es de alguna utilidad? La respuesta es afirmativa. La simplicidad de esta idealización nos permite entender fácilmente los modelos, sus propiedades y generar resultados de más o menos general aplicación. Después, con una progresiva eliminación de los anteriores supuestos, podemos ir encontrando resultados más acordes a la realidad. De hecho, la eliminación o debilitamiento de algunos de los supuestos es fuente cotidiana de investigación en finanzas. Además, mientras más cercanos a la realidad, más difíciles de estudiar son los modelos.

Lo importante es observar los resultados que se obtienen a partir de los modelos, cuando les aplicamos lógica y la teoría matemática apropiada, por lo que realmente significan, y nunca olvidar los supuestos que se utilizaron para obtenerlos.

El objetivo de este artículo es presentar dos modelos matemáticos para valoración de opciones, desarrollar las teorías pertinentes y mostrar cómo esas teorías⁶ son imágenes simplificadas de teorías más complejas. El proceso es gradual en cuanto a dificultad y su núcleo está basado en las ideas del profesor Thomas Bjórk.

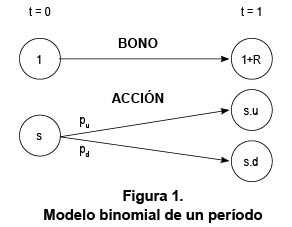
El primero y el más sencillo de los modelos: Modelo Binomial de un período

En este modelo consideramos dos instantes de tiempo: hoy (t = 0) y mañana (t = 1), y dos activos financieros: un bono y una acción. Los activos están relacionados con dos procesos de apreciación: un proceso determinístico para el bono y un proceso estocástico para la acción {S₀=s, S₁}. El precio de la acción inicialmente es s y tiene dos estados de la naturaleza posibles en t = 1 a saber: s.u y s.d, donde d < u⁷. Con el fin de facilitar los cálculos, utilizaremos como unidad el precio de un bono en el tiempo t = 0.

Suponemos la existencia de una medida de probabilidad P, llamada la probabilidad objetiva, de tal manera que P(S₁ = s.u) = p_u y P(S₁ = u.d) = p_d donde p_u + p_d = 1. Además, una tasa de interés, R, la tasa libre de riesgo, de tal manera que en t = 1 el valor del bono es (1+R) veces su valor en t = 0, es decir, de acuerdo con las unidades que vamos a utilizar, 1+R.

R, u, d, p_u y p_d se suponen constantes.

Podemos representar el modelo de una manera gráfica como se muestra en la figura 1.

Portafolios

En este contexto, un portafolio es un par ordenado (o un vector de dos dimensiones) h = (x, y) donde x es el número de unidades del bono e y es el número de unidades de la acción en el portafolio.

Supondremos que es posible tomar posiciones cortas en ambos, el bono y la acción. Para clarificar esto, es conveniente a veces pensar en el bono como en un banco con una tasa de interés R.

Así, tomar una posición corta indica prestar plata en el banco para devolverla con su respectivo interés. En este caso el equivalente a un bono es $1.

También haremos la muy importante suposición de que nuestras posiciones pueden ser fracciones cualesquiera; esto significa que x e y pueden tomar cualquier valor real y que el conjunto de todos los portafolios posibles es el plano XY o sea el espacio bidimensional R². Por ejemplo, h = (-2.3, 5) significa que tomamos prestados del banco $2.3 y compramos 5 acciones; h = (3.5, -1/2) significa que guardamos en el banco el valor $3.5 y tomamos una posición corta en media acción.

Procesos de valor y portafolios de arbitraje

Definiremos los procesos que asociamos con el bono y con la acción.

Definición 1 (Procesos de valor)

Sea h = (x, t) un portafolio dado (que comienza en t = 0), su proceso de valor, que se denota mediante V^h_t se define mediante V^h_o= x + y.s, V^h_t (1+R) x + y.s₁ (1)

El significado del proceso estocástico de valor es claro: en t = 0, el valor del portafolio es la suma del valor de x bonos más el valor de y acciones (cada una vale el equivalente a s bonos); en t = 1 el valor de cada bono es (1+R) y el valor de cada acción es s₁ que es una variable aleatoria. En t = 1 el valor del portafolio es uno de los elementos del siguiente conjunto {(1+R)x + y su, (1+R)x + ysd} que, junto con el estado inicial, forman el espacio de estados del proceso.

Intuitivamente hablando, un portafolio de arbitraje es una "maquinita para hacer plata a partir de nada" y, aunque la siguiente definición parece algo extraña, es muy útil en la deducción de resultados⁸.

Definición 2. (Portafolio de Arbitraje)

Un portafolio de arbitraje es un portafolio h = (x,y) que satisface:

V^h₀= 0 y > 0, con probabilidad 1. (2)

La existencia de un objeto de estos se considera un caso serio de mala valoración en el mercado. Cuando no existe posibilidad de ellos se dice que el mercado es libre de arbitraje.

En teoría financiera es muy importante conocer las condiciones que determinan un mercado libre de arbitraje. A continuación enunciamos una condición necesaria y suficiente para nuestro primer modelo:

Proposición 1.

El modelo binomial de un período es libre de arbitraje si y solo si d ≤ 1+R ≤ u.

Interpretación: La propiedad anterior significa que ninguno de los dos activos domina al otro en el sentido que si un inversionista tiene una cierta cantidad de dinero, es imposible para él o para ella saber por adelantado si debe invertir todo el dinero en el bono (o guardarlo en el banco) o todo el dinero en la acción y tener una ventaja segura con respecto a otro inversionista que siga la estrategia contraria.

Prueba de la proposición:

Como la proposición es del tipo "si y solo si", haremos la prueba en dos direcciones:

1. Ausencia de arbitraje implica d ≤ 1 + R ≤ u, y

2. d ≤ 1+ R ≤ u implica ausencia de arbitraje

Ahora, el enunciado 1 es equivalente a "si no se cumple d ≤ 1+ R ≤ u entonces es posible el arbitraje" y éste es el que utilizaremos⁹.

Si d ≤ 1+ R ≤ u no se cumple entonces debe ser u < 1+ R ó 1 + R < d.

Primera consideración: Si u < 1+ R, entonces tenemos d < u < 1+ R. Creemos el siguiente portafolio h =(s, -1), con s > 0, entonces V^h₀= s + (-1) s = 0, y

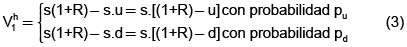
Así que V^h₁ > 0 con probabilidad 1, es decir h es un portafolio de arbitraje.

En un lenguaje más sencillo, el argumento se puede resumir como: partiendo de cero, vender corta la acción y colocar el dinero en el banco y al final del período tendremos suficiente para comprar la acción y reponerla y ade más quedará un excedente.

Segunda consideración: Si 1 + R < d, entonces 1 + R < d < u. Creemos el siguiente portafolio h =(-s, 1), con s > 0, entonces, V^h₀ = -s + s = 0 (de nuevo) y en t = 1, tendremos

En palabras más sencillas, en esta otra situación, partiendo de cero, prestamos el valor de una acción en el banco, compramos la acción y al terminar el período tendremos con qué pagarle al banco y nos quedará un excedente.

En ambos casos observemos que hay dominancia de uno de los activos sobre el otro. Los dos argumentos demuestran la primera parte de la proposición.

Demostremos ahora la segunda parte:

Supongamos que d ≤ 1 + R ≤u y sea h = (x, y) un portafolio tal que V^h₀= x + y.s = 0, entonces x = -ys, y por lo tanto h= (-y.s, y), entonces,

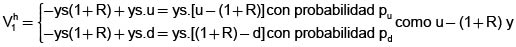
(1-R)-d son números positivos, es imposible que V^h₁ sea positivo en ambos casos, independientemente del signo de y, y por lo tanto es imposible que V^h₁ sea positivo con probabilidad uno. En otras palabras, no existen posibilidades de arbitraje.

La tasa libre de riesgo como una combinación convexa de u y d

Uno de los conceptos más importantes en economía matemática es el de combinación convexa. Si 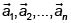son elementos en Rⁿ, una combinación convexa de esos elementos es cualquier objeto de la forma 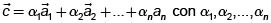números reales no negativos tales que 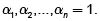Este concepto es una generalización de la noción de promedio ponderado o media ponderada y tiene un papel fundamental en optimización.

Fácilmente podemos comprobar que si d ≤ 1 + R ≤ u, entonces existen α₁ y α₂, tales que α₁u + α₂d = 1 + R y α₁ + α₂ = 1, es decir, 1+R es una combinación convexa de u y d, es mas, fácilmente podemos encontrar que 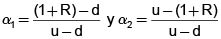y que estos valores son únicos.

Medida Martingala¹⁰

Dada la naturaleza de α, y α₂, se pueden considerar como las probabilidades de u y d, q_u y q_d respectivamente, bajo una nueva medida de probabilidad Q, diferente de la probabilidad objetiva, P, que consideramos anteriormente. Es decir, 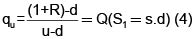y además 1 + R = q_d.d + q_u.u. A esta medida de probabilidad se le llama Medida Martingala, Medida Neutral Respecto al Riesgo o Medida Ajustada por Riesgo.

La propiedad más importante de estas medida de probabilidad es la siguiente: sea E^Q el valor esperado según esta medida, 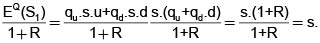con la unicidad de la medida de probabilidad nos servirá para definir la nueva medida de probabilidad.

Definición 3 (Medida Martingala)

Sea Q una medida de probabilidad asociada al modelo binomial, se dice que Q es la medida martingala si se cumple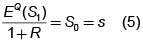

Es decir, la medida martingala es la medida de probabilidad bajo la cual el valor esperado de la acción en t =1, descontado a t = 0, es igual al valor de la acción en t = 0.

Dos importantes propiedades de la medida martingala:

Proposición 2

La medida martingala es única¹¹.

Proposición 3

Una condición necesaria y suficiente para que el mercado esté libre de arbitraje es la existencia de una medida martingala.

Prueba:

Observemos lo siguiente: Se cumple d ≤ 1 + R ≤ u si y solo si, el mercado está libre de arbitraje. Ahora, si se cumple d ≤ 1 + R ≤ u, existe la medida martingala (la definimos a partir de acá) y si existe la medida martingala, dado que 1 + R = q_d.d + q_u.u, entonces debe suceder que d ≤ 1 + R ≤ u. Por lo tanto, d ≤ 1 + R ≤ u si y solo si, existe la medida martingala.

Ejemplo 1

Consideremos una acción que vale $1200 en t = 0 y que en t =1 puede valer $1020 con probabilidad 0.45 ó $1500 con probabilidad 0.55¹². Fácilmente podemos encontrar que d = 0.85 y u = 1.25. Consideremos una tasa libre de riesgo del 20% para el período, es decir, 1+ R = 1.2, entonces, debido a que 0.85 ≤ 1.20 ≤ 1.25, el mercado esta libre de arbitraje. La medida martingala está dada por 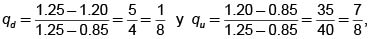con esta medida

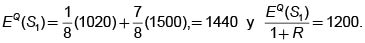
Supongamos que la tasa libre de riesgo fuera del 28%, 1 + R > u, entonces venderíamos las acciones y pondríamos el dinero en el banco y con seguridad tendríamos una ventaja sobre cualquiera que tuviera acciones. El problema es que, a la larga, otros descubrirían la estrategia y nadie compraría acciones.

Derivados o reclamaciones contingentes

Son contratos financieros que dependen de un activo subyacente, por ejemplo, una opción para comprar una acción en cierto momento y por cierta cantidad, da el derecho, mas no la obligación de comprarla bajo esas circunstancias. Matemáticamente estos contratos son funciones del precio del activo subyacente y más específicamente, del proceso estocástico que rige el precio, en nuestro modelo serán funciones del proceso que rige el precio de la acción.

Definición 4 (Derivados)

Un derivado o reclamación contingente es cualquier variable aleatoria X de la forma X = Φ(Z) donde Z es la variable aleatoria que rige el precio en el modelo. La función Φ se llama función del contrato.

En nuestro modelo la variable aleatoria Z toma los dos valores u y d.

Ejemplo 2: Una opción "call" europea¹³

Consideremos el siguiente derivado llamado opción "call" europea: un contrato que da el derecho, pero no la obligación, de comprar en el tiempo t = 1 una acción por el valor $K (precio de ejercicio). Para que tenga sentido, debe cumplirse s.d < K < s.u. Si en t =1 el precio de la acción es s.u, el propietario del contrato compra la acción por $K e inmediatamente la vende por s.u obteniendo un beneficio de s.u – K. Si el precio de la acción es s.d, no tiene ningún sentido ejercer la opción¹⁴.

En este caso la variable X está dada por 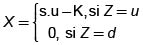y la función del contrato está dada por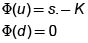

El problema de apreciación

Desde el punto de vista financiero la pregunta más importante es: ¿Cuál es el precio "justo" (en algún sentido) del derivado en el instante t = 0≤

Denotemos el precio de X en el instante t mediante Π(t; X), entonces nuestro problema consiste en hallar Π(0;X). La metodología que vamos a utilizar nos va a llevar a dos de las nociones más importantes en finanzas: Cobertura y completitud. Comenzaremos con unas definiciones.

Definición 5 (Portafolios de cobertura)

Sea X un derivado, se dice que X es replicable si existe un portafolio h = (x, y) tal que V^h₁ = X con probabilidad 1. Si existe tal portafolio h se le llama un portafolio de cobertura o portafolio replicador.

Definición 6 (Mercados completos)

Si todos los derivados son replicables se dice que el mercado es completo.

¿Qué es lo que hace importante al portafolio replicador?

Primero, desde el punto de vista financiero, poseer el contrato (derivado) y poseer el portafolio replicador son equivalentes.

Segundo, el portafolio como construcción matemática nos ayudara a obtener el precio de la reclamación.

Proposición 4 (El portafolio de cobertura como determinante del precio del derivado)

Supongamos que el derivado X es replicable con un portafolio h = (x, y), entonces cualquier precio en t = 0, diferente de V^h₀ lleva implícita una posibilidad de arbitraje.

Prueba

En vez de una prueba rigurosa, daremos una argumentación en forma semi-intuitiva¹⁵. Sea Π(0,X) el precio del derivado en t = 0.

1. Si Π(0, X) > V^h₀ (el precio del derivado es superior al valor del portafolio), entonces podemos vender el derivado, comprar el portafolio y colocar la diferencia D en el banco. En t =1 tendremos V^h₁ + (1+R)D.

2. Si V^h₀ > Π(0,X) (el precio del portafolio es superior al del derivado), entonces podemos vender el portafolio, comprar el derivado y colocar la diferencia, D₁, en el banco. En t =1 tendremos V^h₁ +(l+R)Dr

Como en cada caso tenemos oportunidades de arbitraje, la tínica posibilidad que es consistente con un mercado libre de arbitraje es Π(0,X)= V^h₀

Imposibilidad de arbitraje y completitud

Otra característica importante de los mercados libres de arbitraje es que son completos. Ése es el contenido de la próxima proposición.

Proposición 5 (Los mercados libres de arbitraje son completos)

Si el mercado del modelo binomial de un período es libre de arbitraje, entonces es completo.

Prueba

Sea X un derivado arbitrario, fijo, con función de contrato $. Debemos probar que X es replicable, es decir, necesitamos encontrar un portafolio h=(x,y) que cumpla V^h₁ = Φ(u) si Z=u, y V^h₁= Φ(d) si z = d. En otras palabras, queremos que (1+R)x + u.sy = Φ(u) (a) y (1+R)x + d.sy = Φ(d) (b). Resolviendo este sistema para x y para y obtenemos .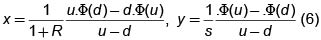

Estos son los valores que constituyen el portafolio replicador del derivado X.

El portafolio replicador y la medida martingala

Si expresamos el valor del portafolio replicador V^h₀= x + s-v usando (6) obtenemos

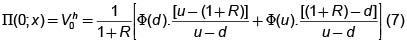
y este es el valor esperado del derivado en t =1, usando la medida martingala, descontado a t =0, que se puede escribir como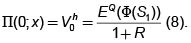

Esta fórmula es la análoga, dentro de este modelo, a la fórmula de Black-Scholes para apreciar derivados en tiempo continuo.

Apreciación y actitud ante el riesgo

De acuerdo con la noción de utilidad de Von Neumann y Morgernstern¹⁶, los tomadores de decisiones racionales se clasifican en tres categorías: Amantes del riesgo, neutrales respecto al riesgo y los que sienten aversión hacia el riesgo. Los que toman decisiones con base en el valor esperado de los resultados de sus decisiones son los neutrales respecto al riesgo¹⁷. Es por esto que la formula (8) se llama también fórmula de valoración neutral respecto al riesgo y a la medida martingala se le llama medida neutral respecto al riesgo. Si embargo, debemos ser precisos en que ninguno de nuestros supuestos se refiere a la actitud ante el riesgo.

Ejemplo 3

Consideremos una opción cali europea, sobre una acción que vale actualmente $1200, con un precio de ejercicio de K =$1300 y u = 1.25, d = 0.85 y una tasa libre de riesgo del 20% por el período. El portafolio replicador está dado por

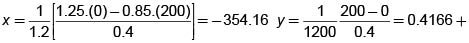
Esto significa prestar $ 354.16 del banco y comprar el 41.66% de una acción. Esto nos da el valor neto –354.16 + 0.4166 * 1200 = 145.83. Este es V^h₀ y el valor de la opción. si usamos (7) en vez de (6) obtenemos 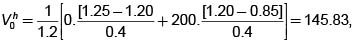y si usamos (8) con las probabilidades de la medida obtenemos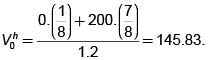

Un segundo modelo: El modelo binomial multiperíodo

Extendamos nuestras nociones a un modelo discreto en el que el índice temporal t toma los valores t = 0, 1, . .,T y T, el horizonte, es fijo. Tenemos únicamente dos activos: un bono con proceso de precio {B_t} y una acción con proceso de precio {S_t} que no paga dividendos durante ese lapso de tiempo de 0 a T. También suponemos una tasa de interés de corto plazo R, determinística.

Tomando el precio inicial como unidad, la dinámica del precio del bono se puede expresar mediante la ecuación en diferencias B_n+1= (l+R)B_n (9), que significa simplemente "el valor actual es igual al valor anterior más los intereses", y el valor inicial B₀=1. La dinámica de la acción está dada por la ecuación estocástica "en diferencias" S_n+1 = S_n.Z_n (10),"valor actual igual al valor anterior multiplicado por una constante aleatoria" con la condición inicial S₀=s, donde Z₀, Z₁,.. .,Z_T–1 son variables aleatorias independientes e idénticamente distribuidas que pueden tomar únicamente los valores u y d, u < d, con probabilidades P(Zn=u) = p_u y P(Zn=d)=p_d, para n =0,1, . . ,T-1.

Como se espera que el precio de la acción baje y suba de manera aleatoria, es natural suponer d < 1 < u. Si hacemos e<σUB>1= u-1 y e<σUB>2 = d-1, entonces u = 1+ e<σUB>1 y d = 1+e<σUB>2, por lo tanto, la expresión (10) se puede escribir como S_n+1= S_n(1+e<σUB>1) ó S_n+1 = S_n(1+e₂) lo que lleva a la expresión ΔS_n = S_n+1 = S_n = S_nΔW_n (11), donde ΔW_n es una variable aleatoria que puede tomar los valores e₁ ,con probabilidad p_u ó e₂, con probabilidad p_d. La ecuación (11) es un caso particular de la ecuación en diferencias, estocástica ΔS_n = u.S_n.Δt + σ.S_nΔW_n (12), donde μ y σ son constantes y Δt es la diferencia entre dos instantes consecutivos. La ecuación (12) es la análoga discreta de la ecuación diferencial estocástica del movimiento browniano geométrico que se asume en la teoría de Black y Scholes como modelo del comportamiento del precio de las acciones.

El árbol de la figura 6 muestra las posibles trayectorias del proceso de precio para un horizonte T = 3. Un proceso de este tipo se llama un paseo aleatorio. Debemos notar que las probabilidades del estado final son independientes de la trayectoria. De un árbol de este tipo se dice que es recombinante. En la valoración de algunos derivados más complejos, como las opciones asiáticas, hay que considerar dependencia de la trayectoria.

Ahora presentaremos unas definiciones y propiedades del modelo multiperíodo como generalización del modelo de un solo período.

Definición 7 (Estrategia de portafolio)

Una estrategia de portafolio es un proceso estocástico {h_t= (x_t,y_t); t = 1,...,T} tal que h_t es una función de S₀, S₁, ... , S_T–1. Por convención se establece h₀=h₁.

El proceso de valor {V^h_t}, correspondiente a la estrategia de portafolio se define mediante V^h_t = x_t(1 + R) + y_tS_t (13).

Interpretación: x_t es la cantidad de dinero que depositamos en el banco en el tiempo t-1 y mantenemos allí hasta el tiempo t. y_t es el número de acciones que compramos en t-1 y mantenemos en el portafolio hasta t. Así, V es el valor del portafolio que poseemos desde t-1 hasta t. Este portafolio es contingente en el sentido que depende de la infamación que hemos recolectado sobre la acción desde el instante 0 hasta t, y es dinámico porque su composición va cambiando con el tiempo.

Definición 8 (Portafolios autofinanciados)

Una estrategia de portafolio se dice que es autofinanciada si satisface x_t.(1+R) + y_t.S_t = x_t+1 + y_t+1S_t+1, para t = 0,1, . . .T-1.

Esto significa que al portafolio no se le hacen inyecciones ni extracciones de fondos en ningún momento. El dinero para depositar en el banco y comprar acciones en el instante t+1 ("portafolio nuevo"), se obtiene del dinero en el banco (más los intereses) en el tiempo t y de la venta de acciones que se tenían durante el periodo t hasta t+1 ("portafolio viejo"). El mantener algunas de las acciones en el portafolio se puede interpretar como venderlas e inmediatamente volverlas a comprar.

Definición 9 (Oportunidad de arbitraje multiperíodo)

Una posibilidad de arbitraje es un portafolio autofinanciado h que satisface V^h₀ = 0,P(V^h_t>0) = 1, y P(V^ht ≤ 0)>0 (14).

De nuevo, un portafolio de arbitraje es una posibilidad de hacer dinero sin riesgo de pérdida.

Definición 10 (Medida de probabilidad martingala)

Las probabilidades de la medida martingala Q, q_u y q_d (ó Π_u y Π_d según otras notaciones) se definen como las probabilidades para las cuales se cumple la relación 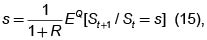para t = 0, ... , T–1.

Con base en esta definición, podemos calcular fácilmente estas probabilidades dado que

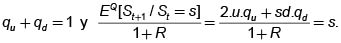
Al resolver el sistema de ecuaciones obtenemos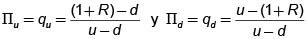

que coinciden exactamente con las probabilidades del modelo anterior.

Definición 11 (Reclamaciones contingentes simples)

Un derivado o reclamación contingente simple es una variable aleatoria X de la forma X = Φ(S_T) donde la función del contrato Φ es una función de valores reales dada.

En este segundo modelo es importante hacer énfasis en que derivado simple significa que X depende solo del valor de la acción en el tiempo T y no de otros valores que haya podido tener antes.

El problema de la valoración

El problema principal es encontrar un proceso de precio "razonable" {Π(t, X); t = 0,1,..., T} para el derivado X. Es decir, debemos ser capaces de darle un valor al derivado, no sólo en el instante inicial, sino en cualquier instante hasta T.

Una solución al problema

La solución al problema de valoración o apreciación también la daremos en este caso utilizando un portafolio replicador.

Definición 12 (Portafolio replicador)

Un derivado X es replicable si existe un portafolio autofinanciado h={h_t = (x_t,y_t); t =1,.. .,T} tal que V^h_t = X con probabilidad 1. En este caso se dice que h es un portafolio replicador o un portafolio de cobertura para X. Si todos los derivados del mercado son replicables se dice que el mercado es completo (en un sentido dinámico).

Proposición 6 (El portafolio replicador como solución)

Supóngase que X es replicable mediante el portafolio h. Supóngase además que en el tiempo t es posible comprar el derivado a un precio menor que (o venderlo a un precio superior a V^h_t). Entonces es posible conseguir una ganancia de arbitraje.

Prueba

Podemos justificar la proposición mediante el siguiente argumento:

Si es posible comprar, en el tiempo t, el contrato X a un precio p < V^h_t, entonces podemos vender corto el portafolio, comprar el contrato y depositar V^h_t–p en el banco. Al llegar el tiempo T hacemos la reclamación sobre el activo subyacente y la entregamos al dueño del portafolio obteniendo V^h_t–p más los intereses, como ganancia de arbitraje. Si es posible venderlo a un precio superior a V^h_t, el argumento es similar.

Como consecuencia de todo esto tenemos el siguiente principio:

Principio de valoración para una reclamación simple X

El único proceso de precio apropiado, en el sentido de no arbitraje, para el derivado simple X está dado por Π(t,X) = V^h_t, para t =0, 1, ... , T.

El algoritmo binomial

Dado el anterior principio de valoración, lo único que nos falta por conocer es un procedimiento que nos permita calcular el precio del portafolio replicador en cualquier instante. Este procedimiento se llama Algoritmo Binomial. Para desarrollarlo necesitamos una notación especial: para cada nodo del árbol binario, en el tiempo t, se tiene que S_t=s.u^k.d^t-k, donde k es el número de "movimientos hacia arriba del precio de la acción", o el número de ocurrencias del resultado u, a través de cualquier trayectoria que lleve a uno de esos nodos. Así que cada uno de esos nodos se puede denotar mediante el par by (t, k), k = 0,1, . .,T. Por ejemplo, los nodos del último nivel de la derecha en el árbol de la figura 6 se denotan, de arriba hacia abajo, mediante (3, 3), (3,2), (3,1) y (3,0), respectivamente. Además, el precio del portafolio en el nodo (t, k) se denotará mediante V_t(k).

Proposición 7 (Algoritmo binomial)

Considérese el derivado simple X= Φ(X_T) que se puede replicar mediante el portafolio autofinanciado h. El valor del portafolio en el nodo (t, k), V_t(k) se puede calcular recursivamente hacia atrás mediante el siguiente esquema:

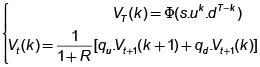si t = t–1, ..., 0 (16) donde las probabilidades de la medida martingala q_u y q_d están dadas por 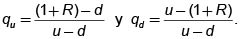el portafolio replicador en el tiempo t, h_t = (x_t, y_t) está dado por 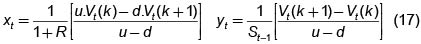para t = T–1, ..., 0. En particular, el precio, libre de arbitraje, del derivado en el tiempo t = 0 está dado por V₀(0).

Ejemplo 4

Consideremos una tasa libre de riesgo del 7% por período, un horizonte T=3 , d = 0.85, u = 1.2 y una opción cali europea sobre una acción que vale actualmente (t=0) $1200, con un precio de ejercicio de $1500 = K.

Como los posibles valores de la acción en los nodos de tercer nivel son $273.60, $1468.80, $1040.40 y $736.95, entonces V3(3) = 573.60, V3(2) = 0, V3(l) = 0, V3(0) = 0. Las probabilidades de la medida martingala son

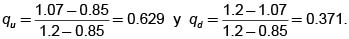Con base en estos valores encontramos

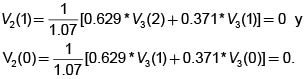
Con base en los anteriores encontramos

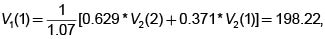
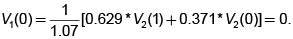Y finalmente,

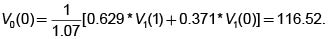éste es el valor de la opción.

En la figura 7 se pueden observar las posibles trayectorias del proceso de precio, y los precios del portafolio replicador. Utilizando las expresiones (17) calculamos la composición del portafolio en cada nodo no terminal.

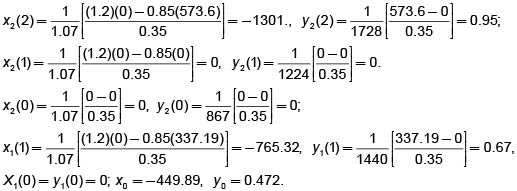
En la figura 7 se muestra también la composición del portafolio de cobertura cuando sus componentes son diferentes de cero.

La prueba de la proposición 7 es algo engorrosa, aunque las fórmulas (17) son fácilmente deducibles. Sin embargo, invitamos al lector a realizar la reconstrucción del algoritmo para el caso T=2, esto ayudará grandemente a la comprensión del porqué del algoritmo general.

Muchas veces no necesitamos los precios del portafolio en cada instante sino únicamente en t = 0. Para estos casos, la fórmula que enunciamos a continuación es mucho más práctica que el algoritmo general.

Proposición 8 (Fórmula de valoración)

El precio libre de arbitraje del derivado, en el tiempo t = 0 está dado por

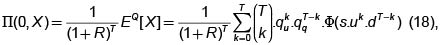donde Q es la medida martingala y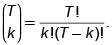

El lado izquierdo de (18) es el análogo, dentro del modelo binomial multiperíodo, de la fórmula de valoración de Black-Scholes: El valor descontado a t = 0 del valor esperado del derivado X según la medida martingala.

Ejemplo 5

Observando la figura 7 vemos que el valor esperado se calcula con los valores del derivado en el último nivel del árbol. Como allí todos los valores excepto el correspondiente a k =3 son cero y T =3, el valor esperado es 0.629³ x 573.60 = 142.74 y el valor descontado a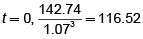

El lector con conocimiento de distribuciones de probabilidad seguramente habrá identificado la expresión 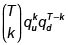con las probabilidades asociadas a una variable aleatoria binomial con parámetros T (número de pruebas) y q_u (probabilidad de éxito en cada prueba).

Terminamos de exponer este modelo enunciando una proposición y el teorema que presenta el resultado capital de esta teoría. Dejamos al lector la justificación de ambos.

Proposición 9 (condición necesaria y suficiente para la ausencia de arbitraje)

La condición d < 1 + R < u es necesaria y suficiente para la ausencia de arbitraje en el modelo binomial multiperíodo.

Teorema (Completitud del mercado)

El mercado del modelo binomial es completo, es decir, toda reclamación contingente es replicable mediante un portafolio autofinanciado.

Hacia un modelo de tiempo continuo

Si en nuestro modelo multiperíodo consideramos que la tasa libre de riesgo del banco se compone continuamente, entonces sustituimos 1+R por e^r, para un retorno, r, adecuado. Las probabilidades de la medida martingala se calculan como 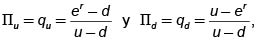y la fórmula de valoración (18) se transforma en 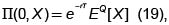que se parece muchísimo más a la fórmula de Black-Scholes¹⁸.

Supongamos ahora que la unidad de tiempo no es 1 sino cierto Δt = h > 0, de tal manera que t toma los valores 0, h, 2h,..., nh =T y que el precio de la acción está regido por S_t+1= S_t. Z(t), donde Z(t) puede tomar los valores 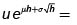con probabilidad ¹/₂ y 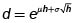con probabilidad ¹/₂, donde μ y σ son constantes positivas¹⁹. Si 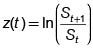entonces, el valor esperado y la varianza de

z(t) son, respectivamente E[z(t)] = μhy var[z(t)] = σ²h. El retorno esperado μh se llama comúnmente "la tendencia", porque es el valor relativo al cual el precio de la acción se tiende a incrementar antes de recibir un "impacto aleatorio" que lo afectará en σ≤h ó en – σ≤h. Al factor σ se le llama comúnmente "la volatilidad", porque refleja el efecto de los impactos aleatorios sobre el precio.

Consideremos el comportamiento del precio de la acción en el lapso desde t = 0, hasta nh = T. Si durante ese lapso de tiempo han ocurrido k movimientos "hacia arriba" y n-k movimientos hacia abajo, entonces

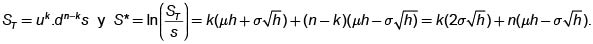
Como k es el número de "éxitos "de la variable aleatoria binomial con n pruebas y probabilidad de éxito 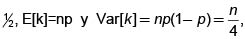por lo tanto 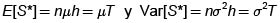que eran resultados esperados dado que S* es la suma de n variables aleatorias independientes e idénticamente distribuidas. Dado que a medida que aumenta n no sólo se agregan elementos a esta suma sino que los valores que pueden tomar u y d cambian, en el paso al límite utilizamos una variante del Teorema Limite Central que traducida a nuestro contexto dice si 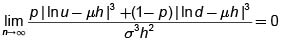²⁰ entonces la distribución de 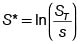tiende a la distribución de una normal con media μT y la varianza σ²T. Y esto es válido apra cualquier instante de tiempo t. Esto quiere decir que la distribución de S_T/s es log normal. Este es uno de los fundamentos del modelo de Black-Scholes.

El verdadero tratamiento en el caso continuo

La deducción anterior es básicamente heurística. Si necesitamos estudiar de manera profunda la valoración de derivados en tiempo continuo, inevitablemente necesitamos recurrir al cálculo estocástico, en especial, al cálculo de Itô y ecuaciones diferenciales estocásticas de Itô.

Por ejemplo, en el caso más elemental, el mercado consta de un bono sin cupones y una acción que no paga dividendos. Sus procesos de precio están dados por la ecuación diferencial determinística dB= r.Bdt (20) y la ecuación diferencial estocástica dX = μXdt + σXdW (21), donde W es un proceso de Wiener²¹ y r es la tasa libre de riesgo para intervalos cortos²².

Dentro de este nuevo marco tenemos los siguientes hechos importantes:

1. El valor de la opción es también el valor esperado según la medida martingala descontado al instante inicial.

2. La existencia de la medida martingala está garantizada por el teorema de Girsanov y está caracterizada por una ecuación diferencial estocástica semejante a (21).

3. Las soluciones de la ecuación (21) son procesos continuos de Markov, es decir, procesos en los que el pasado y el futuro son independientes, dado que conocemos el presente.

4. El proceso estocástico del precio de la acción es un proceso log normal.

5. La única función simple del tipo F(t, S(t)) para el precio de un derivado simple Φ(S(T)) que es consistente con la ausencia de arbitraje es la solución al problema de valor en la frontera

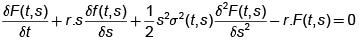²³ (22)

F(t,s) = Φ(s)(23) en el dominio [0, T] x R⁺.

6. La relación de la solución del problema anterior con las ecuaciones diferenciales estocásticas del tipo (21) está dada por el teorema de Feynman-Kac.

7. El portafolio replicador autofinanciado es un proceso estocástico continuo cuyo proceso de valor V^h(t) satisface la ecuación diferencial dV^h(t) = r.V^h(t)dt. Como esta ecuación no tiene el término en dW, se dice que el portafolio es localmente libre de riesgo.

8. El precio libre de arbitraje del derivado simple, en cualquier instante t está dado por F(t,s) = e^–r(T–t)E^Q_t,s(Φ(S(T)))(23), donde el valor esperado se calcula según la medida martingala y el subíndice en el símbolo de valor esperado significa que conocemos el valor s que toma la acción en el tiempo t.

9. El modelo elemental del mercado de un bono y una sola acción es completo y libre de arbitraje.

10. El modelo general del mercado es libre de arbitraje si y solo si, el número de activos subyacentes (que involucran riesgo) que se negocian en él, es menor o igual que el número de procesos aleatorios que afectan los precios.

11. El modelo general del mercado es completo si y solo si, el número de activos subyacentes (que involucran riesgo) que se negocian en él, es mayor o igual que el número de procesos aleatorios que afectan los precios.

12. El modelo general del mercado es completo y libre de arbitraje si y solo si, el número de activos subyacentes (que involucran riesgo) que se negocian en él es igual al número de procesos aleatorios que afectan los precios.

Modelos que superan las limitaciones del modelo de Black y Scholes

Si se quiere mejorar la eficacia de los modelos anteriores es necesario relajar algunos de los supuestos fundamentales, por ejemplo el que la volatilidad a o la tasa de interés r sean constantes. Obviamente al hacer estos cambios los modelos se hacen más complicados.

Entre los modelos continuos se encuentran los de Hull-White (1987), Scott (1987), Stein-Stein (1991), Ball-Roma(1994) y Heston(1993), Eberlein y Prause (1998), Bellalah, Ahnani y Prigent (1999) entre otros. En estos la volatilidad es aleatoria y se representa mediante una función positiva de un proceso estocástico que es generalmente un proceso lognormal, un proceso de Ornstein-Uhlenbeck, un proceso de Cox-Ingersol-Ross (CIR)²⁴. O como en el caso del modelo de Eberlein y Prause, especializado en la microestructura de la valoración, se utilizan procesos de Levy, que son discontinuos. Los modelos de Ball-Roma y Heston son ejemplos de los llamados mean-reverting processes²⁵.

Existen también los modelos estocásticos discretos para la volatilidad. Entre ellos están, los populares modelos ARCH²⁶ (Engle 1982), GARCH²⁷ (Bollerslev 1986,1998), y extensiones de estos EGARCH, IGARCH, FIGARCH, etc. (varios, finales de los 80s y década de los 90s), los llamados modelos de volatilidad estocástica (SV sus iniciales en inglés) introducidos por Taylor en 1986, que corrigen algunas de las limitaciones de los anteriores(Actualmente se trabaja en métodos más eficientes para la estimación de parámetros de este último) y los modelos de conmutación de regímenes²⁸ (Hamilton 1989).

El modelo clásico de valoración supone una estructura de lapsos de las tasas de interés²⁹ que es plana, es decir las tasas de interés de corto y largo plazo son iguales. Actualmente modelos estocásticos para las tasas de interés y algunos de éstos están incorporados en modelos de valoración de activos.

El lector podrá imaginar la cantidad de modelos que han aparecido a partir del modelo original de B-S.

Ninguna generalización es gratuita; se hace siempre con algún costo, y estos modelos no son la excepción. Por ejemplo, la introducción de una volatilidad no constante implica tanto la incompletitud del mercado como la no unicidad de la medida martingala: No siempre es posible replicar un derivado con solo el bono (o el banco) y el activo subyacente y además dada una medida martingala, existe una clase de medidas equivalentes y por lo tanto hay que recurrir a observar cuál medida seleccionó el mercado.

Otros métodos de valoración

En la valoración de activos financieros y la ingeniería financiera en general se han utilizado y se siguen utilizando muchísimas herramientas matemáticas de apoyo: Series de tiempo, procesos estocásticos discretos y continuos de diferentes clases, fractales y multifractales y elementos finitos, entre otros (se dice que algunos utilizan herramientas de la mecánica cuántica). Sin embargo lo más importante es tener en cuenta los supuestos que hay detrás de cada modelo. Ello nos evitará la mala interpretación de los resultados y la extrapolación del modelo a campos en los que no representa nada real.

¿Es el modelo binomial sólo una herramienta heurística?

Definitivamente ¡NO! Aunque acá lo presentamos como un medio para acercarnos a la teoría de la valoración o apreciación de los activos financieros. El modelo binomial es una poderosa herramienta computacional para calcular precios de derivados. Existen modificaciones del algoritmo para valorar opciones sobre acciones que pagan dividendos, cuando se tienen pronósticos sobre los mismos. Extensiones del mismo para opciones (europeas y americanas³⁰) sobre un activo subyacente con volatilidad estocástica así como modificaciones para el cálculo del precio de opciones sobre índices, derivados sobre tasas de interés y derivados sobre moneda extranjera, entre otros. En resumen, dominar el modelo binomial es un excelente comienzo en la comprensión de la teoría y la práctica para la valoración de los derivados financieros.

NOTAS:

1 En lenguaje más elemental, "se hace caso omiso".

2 Vendemos "corta" una acción cuando la tomamos prestada, la vendemos a un tercero y después la compramos, a un precio menor, para devolvérsela a su dueño.

3 En la literatura en inglés se le llama bid/ask spread.

4 Market makers.

5 En muchos mercados se establece el tamaño normal del Mercado (NMS:Normal Market Size) de tal manera que los precios que se anuncian son válidos para lotes con un tamaño menor o igual a ése.

6 Acá teoría se toma en el sentido epistemológico de un conjunto de supuestos, definiciones y las consecuencias lógicas de éstos.

7 De las iniciales de up y down.

8 Esta situación es muy común en matemáticas: la definición formal casi nunca tiene interpretación intuitiva fácil y la mejor interpretación intuitiva pocas veces sirve para deducir propiedades importantes.

9 Recordemos que P≤Q, equivale a ¬Q≤ ¬ P.

10 El término se refiere a un tipo de proceso estocástico que es la representación de un juego justo. El proceso (X₁, X₂,. . .) es una martingala si su valor esperado es finito y si cumple la siguiente propiedad del valor esperado condicional E(X_t+1/X₀, X₁, ... ,X_t)= Xt para todo t, es decir, en todo momento el mejor pronóstico para el valor siguiente, dada la información recolectada hasta el presente, es el valor actual. Las martingalas juegan un papel muy importante en la teoría financiera moderna.

11 La prueba de ésta es bastante sencilla e invitamos al lector a hacerla.

12 Si estamos hablando en términos relativos, la acción valdría 1200 veces el valor del bono.

13 Actualmente no existe término en español para designar este tipo de opción.

14 Las opciones "put" dan el derecho de vender la acción.

15 En matemáticas se puede hacer esto en una gran cantidad de casos; pero, generalmente esas argumentaciones son demasiado largas como para escribirlas detalladamente.

16 Este concepto es fundamental en la teoría financiera moderna.

17 Los demás tienen una función de utilidad no lineal.

18 La fórmula que se utiliza en la práctica para valorar opciones cali según el modelo de Black-Scholes es una fórmula desarrollada, a partir de ésta, con base en la distribución de la normal y es la forma operacional de (19), pero como la fórmula (19) captura la esencia del método, con ligeras variaciones, es aplicable a otros derivados.

19 Son posibles otras elecciones de u, d y las probabilidades respectivas.

20 Lo que significa esta propiedad es que a medida que n crece, la importancia del sesgo, relativa a la desviación estándar, se hace cada vez menos importante.

21 Compárense estas ecuaciones con las ecuaciones (9) y (10).

22 Short rate.

23 Ésta se conoce como ecuación diferencial de Black-Scholes.

24 A éstos se les conoce también con el nombre de procesos de Feller.

25 Procesos con retorno hacia la media.

26 Auto_Regressive Conditional Heteroskedastic.

27 Generalized ARCH.

28 Regime Switching Models.

29 Term structure of interest rates.

30 A diferencia de las opciones europeas, las americanas se pueden ejercer antes de la fecha estipulada en el contrato.

REFERENCIAS

Arnold, Ludwig. Stochastic Differential Equations: Theory and Applications. John Wiley & Sons. New York: 1974.

Bjórk, Thomas. Arbitrage Theory in Continuous Time. Oxford University Press. New York: 1998.

Cárcamo, Ulises. Procesos de Wiener. Revista Universidad EAFIT No. 110, Abril, Mayo, Junio de 1998.

Finucane, Tomas J. Binomial Approximations of American Call Options Prices with Stochastic Volatilities. Advances in Futures and Options research. Vol 7.1994.

Franses, Philip Hans y Dijk, Dick van. Nonlinear Time series in Empirical Finance. Cambridge University Press.: 2000.

Gard, Thomas c. Introduction to Stochastic Differential Equations. Marcel Dekker, Inc. New York: 1988.

Jarrow, Robert y Turnbull Stuart. Derivative Securities. Soth-Western College Publishing. Cincinnati, Ohio:1996.