ARTÍCULOS
Diseños muestrales en la investigación
Gonzalo Tamayo*
*Estadístico. Docente Facultad de Economía Industrial Universidad de Medellín
Introducción
Lo que hoy denominamos investigación, se inició en el momento en que el hombre se enfrentó a problemas y, frente a ellos, comenzó a interrogarse sobre el por qué, cómo y para qué; es decir, cuando empezó a indagar sobre las cosas.
Aplicado al campo de la ciencia, la investigación es un procedimiento reflexivo, sistemático, controlado y crítico que tiene por finalidad descubrir o interpretar los hechos y fenómenos, relaciones y leyes de un determinado ámbito de la realidad.
La tarea de un investigador es: "tomar conocimientos del problema que otros pueden haber pasado por alto, insertarlos en un cuerpo de conocimiento e intentar resolverlos con el máximo de rigor y primariamente, para enriquecer nuestro conocimiento. Según eso, el investigador es un problematizado por excelencia".
Mario Bunge
Debido a su creciente utilización en el área de los negocios, especialmente en la investigación de mercados, en contabilidad, auditoría y en otras investigaciones de cualquier índole, se resalta la importancia que tienen los diseños muéstrales en la investigación. Nuestros conocimientos, nuestras actitudes y nuestras acciones estén basadas, en gran parte, en muestras. Esto es igualmente cierto en la vida cotidiana y en la investigación científica.
La correcta aplicación de las técnicas de muestreo se ha hecho indispensable para los profesionales de las ciencias sociales, la administración, las ciencias biológicas y otras en donde, cada día, aumenta la necesidad de diversificar y profundizar los estudios y donde el muestreo, al igual que la inferencia, juegan un papel de gran importancia y utilidad por su carácter de rapidez y economía.
En muchas investigaciones se ha venido prestando poca atención a los problemas de cómo obtener una muestra y cómo sacar conclusiones satisfactorias de sus resultados.
El presente documento intenta proporcionar una conexión entre el análisis de información estadística para la toma de decisiones y el problema práctico de la obtención de datos al que necesariamente se enfrenta el investigador en las diversas áreas del conocimiento. Es un valioso complemento de consulta, en el que se presentan las técnicas de muestreo más utilizadas, para todo aquel que realice investigación.
Elementos de muestreo
Muestreo: Es un procedimiento para conocer algunas características de la población con base en una muestra extraída de ella.
El objetivo de un diseño de muestreo es proporcionar indicaciones para la selección de una muestra que sea representativa de la población.
Ventajas del método de muestreo con relación al censo
1. Costo reducido.
2. Mayor rapidez
3. Mayores Posibilidades: Aquellas encuestas que están basadas en el método de muestreo tienen un mayor alcance y flexibilidad de acuerdo al tipo de información que pueda ser obtenida.
4. El muestreo puede ser más preciso que el censo. Esto es debido a que cuando el volumen de trabajo es reducido se puede emplear personal capacitado al cual se le puede someter a entrenamiento intensivo.
5. Cuando la medición del elemento trae consigo la destrucción o deterioro del mismo (control de calidad). Ej.: Calidad de las bombillas para Flash.
6. Cuando la población sea infinita o tan grande que le quede al investigador físicamente imposible estudiar toda la población.
Casos en que el censo es preferible al muestreo
1. Un tamaño de población reducida.
2. Cuando la varianza de la característica que se está midiendo es muy grande.
3. Cuando los costos del error sean altos (error muestral + error no muestral).
Error: Es de esperarse que ningún estudio sea cien por cien preciso. Siempre existirán diferencias, unas veces muy pequeñas otras muy grandes. Estas diferencias entre la información obtenida a través de un estudio de investigación y la verdadera información es lo que en investigación se conoce como error.
Este error total proviene de dos fuentes: Error Muestral + Error No Muestral.
Error muestral: Este comprende las diferencias ente los resultados de la muestra y el verdadero valor de la población.
Error no muestral: Son todos aquellos errores susceptibles de incurrir a lo largo del proceso investigativo y diferentes a lo que aquí se ha llamado Error muestral.
Mencionemos algunos:
• Error por mala identificación del problema o diferenciación pobre del problema.
• Errores por incapacidad para identificar la información específica requerida.
• Imperfecciones en el diseño del cuestionario.
• Error en la especificación del marco muestral donde Marco muestral es un listado de las unidades muéstrales o listado de todos los elementos de la población.
• El encuestado responde sobre algo que no sabe.
• El encuestado intencionalmente suministra información incorrecta.
• El encuestado suministra información imprecisa, debido a fallas de memoria.
• Sesgos generados por el encuestador al influir con su tono de voz, explicaciones o apariencia personal, en el encuestado.
• Sesgos generados por el encuestador al registrar incorrectamente las respuestas de los encuestados.
• Sesgos generados por el encuestador al desviarse de las instrucciones que se le han dado.
• Errores generados durante la codificación, tabulación, edición, etc.
• Errores en la interpretación de los datos.
Etapas del procesos de muestreo
• Definir claramente la población.
• Especificar el marco muestral.
• Especificar el método de Muestreo (diseño): Muestreo probabilistico y muestreo no probabilistico.
• Determinar el tamaño de la muestra.
• Especificar el plan de muestreo. En éste se definen los procedimientos operacionales para la selección de las unidades muéstrales.
• Seleccionar la muestra.
Métodos de muestreo
De acuerdo con el conocimiento o no que se tenga de la población, el muestreo puede ser:
Muestreo Probabilistico y No Probabilistico.
Muestreo probabilístico
Con éste método es posible determinar la probabilidad que tiene cada elemento de la población de ser escogido en la muestra. Cuando las muestras son aleatorias, se pueden hacer afirmaciones probabilísticas acerca de la población en estudio.
Muestreo no probabilístico
Si se utiliza este método no se puede establecer de una manera exacta la probabilidad de que un elemento de la población participe en la muestra.
Sin embargo, tiene su aplicación en los estudios exploratorios. Cuando las muestras se seleccionen de manera No aleatoria, sólo es posible hacer afirmaciones de tipo descriptivo sobre la muestra.
Los procedimientos No aleatorios de muestreo nunca deben usarse cuando el objetivo del muestreo es hacer inferencias.
Muéstreos probabilísticos
1. Muestreo aleatorio simple (M A.S.)
El M.A.S. es un método de selección de n unidades, sacadas de una población homogénea de tamaño N de tal manera que cada una de las muestras, tengan la misma oportunidad de ser escogidas.
En el M.A.S. la muestra es sacada al azar unidad por unidad.
La muestra puede ser seleccionada utilizando muestreo con reemplazo o sin remplazo.
El muestreo sin remplazo es aquel en el que un número que ha sido sacado no es reemplazado, ya que esto daría lugar a que la misma unidad entrara en la muestra más de una vez.
El muestreo sin remplazo es un caso contrario.
1.1. Tamaño de la muestra para estimar la Media Poblacional. (m).
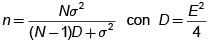
Donde s2 es la varianza Poblacional, N es el numero de elementos de la población, y E es la cota para el error de estimación.
Cuando N es muy grande;
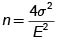
Cuando el objetivo es estimar el Total Poblacional, T, con una cota E para el error de estimación, se debe de sustituir D = EV4N2 en la fórmula del tamaño de muestra.
Para encontrar es necesario conocer la varianza Poblacional. Como dicha varianza (s2) es normalmente desconocida, se hace necesario estimarla utilizando un conjunto de mediciones muéstrales de la población. La varianza puede estimarse con el valor de s2 obtenido en una muestra previa o con el conocimiento del recorrido de las mediciones. Usando el estimador de rango se tiene:
R = 4s lo que implica
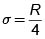
Si el objetivo es estimar la proporción Poblacional p, se hace la varianza s2 = .
Si por algún motivo se desconoce el valor de se supone que tiene un valor de 0.5.
Cómo seleccionar una muestra aleatoria
La mejor manera de seleccionar una muestra aleatoria, es utilizar una tabla de números aleatorios que se construye combinando los números enteros de cero (0) al nueve (9) que no tienen unpa-trón de ocurrencia.
Procedimiento:
1. Enumerar los elementos de la población según el tamaño de ésta.
Ejemplo 1.
Si la población es de N=10000, enumeramos como sigue: 0001,0002,0003, 0000 donde 0001 representa el primer elemento, 0002 el segundo, 0003 el tercero, y el 0000 representa el elemento 10000.
2. De la tabla de números aleatorios se elige un punto arbitrario de partida y siguiendo la secuencia se van determinando los elementos de la muestra.
Si un número aleatorio ocurre dos veces se omite la segunda ocurrencia y se selecciona otro número aleatorio para reemplazarlo.
3. Determinar el valor de los elementos de la muestra.
Ejemplo 2.
Estimador
Si la población es de N=876, enumeramos como sigue: 001,002, 003,..., 876, y se procede en forma similar.
1.2.?Estimación de la media pobla-cional. (m)
Estimador
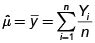
Varianza estimada del estimador
Intervalo de confianza para estimar m
La cantidad 2 garantiza una confianza de por lo menos el 75%, y muy posiblemente del 95%, según que la población sea no normal o normal respectivamente.
1.3.?Estimación del Total Poblacional.(T)
Estimador
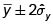
Varianza del estimador 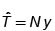Intervalo de confianza para estimar T
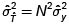
1.4. Estimación de la ProporciónPoblacional. ( p )
Estimador
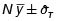
Varianza estimada del estimador.
2. Muestreo estratificado aleatorio (M.E A.)
El M.E.A. se utiliza cuando la población es heterogénea y se tiene un listado de ella.
En esta técnica la población de N unidades es dividida en subpoblaciones o estratos internamente homogéneos: N1,N2,N3,..., NL.Estas subpoblaciones son excluyentes y al reunirlas forman la totalidad de la población.
Para obtener un beneficio completo de la estratificación, deben ser conocidos y especificados los valores de Nh (tamaño de los estratos), con h = 1,2,..., L.
Una vez que han sido determinados los estratos, se saca una muestra de cada una de ellos en forma independiente y que representaremos por n1, r^, rij, ...,
Si se toma una muestra simple aleatoria de cada estrato, el procedimiento completo es conocido como "Muestreo estratificado aleatorio".
Razones para emplear la estratificación
• Cuando se desee información con cierta precisión en algunas subdivisiones de la población, puesto que así se puede tratar cada subdivisión como una población por sí sola.
• Por conveniencias de tipo administrativo.
• Cuando los problemas de muestreo difieren marcadamente en diferentes partes de la población.
• Con la estratificación se obtiene una mayor precisión en los estimadores de las características de toda la población puesto que los estratos son más homogéneos que la población.
2.1. Tamaño de la muestra para la estimación de u..
Utilizando la Afijación proporcional en el que el tamaño de la muestra es proporcional al tamaño del estrato.
donde Nies el número de elementos del estrato i y
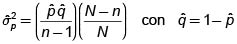
El tamaño de muestra está dado por:
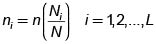
donde 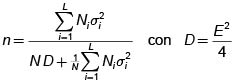son, respectivamente, la varianza y el tamaño del i-ésimo estrato.
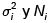puede estimarse por medio de
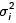o por medio del rango de las mediciones contenidas en el estrato i haciendo
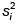lo que implica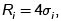
El tamaño de muestra necesario para estimar el Total Poblacional, T, con una cota E para el error de estimación, se obtiene sustituyendo D = E2/4N2 en la fórmula del tamaño de la muestra.
Cuando se usa el muestreo estratificado para estimar la proporción Poblacional se debe de sustituir 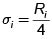para la varianza del estrato i y hacer D = E2/4N2.
es la proporción Poblacional del estrato i que se puede hacer igual a 0.5 cuando no hay posibilidad de conocerla o de ser obtenida.
Estimación de la media y la varianza de cada estrato
donde es la j-ésima observación del estrato i.
2.2 Estimación de la media poblacional (m)
Estimador.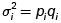
Varianza estimada del estimador
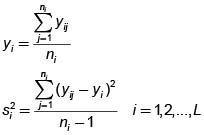
Intervalo de confianza para estimar m.
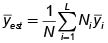
2.3. Estimador del Total Poblacional. (T)
Estimador
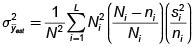
Varianza estimada del estimador
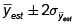
Intervalo de confianza para estimar T.
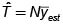
2.4. Estimación de la Proporción Poblacional. ( p )
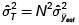
Varianza estimada del estimador.
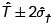
Intervalo de confianza para estimar p.
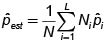
3. Muestreo por conglomerados
El muestreo por conglomerados se utiliza:
• Cuando no existe una lista de todos los elementos de la población, o sería muy costoso obtenerla.
• La población es grande y está dispersa en una región muy extensa.
El procedimiento en el muestreo por conglomerados consiste en dividir la población en M grupos denominados conglomerados.
Después de dividir la población en conglomerados y tener un listado de ellos, se seleccionan al azar algunos de ellos utilizando M.A.S. y posteriormente llevar a cabo un censo completo en cada uno de los conglomerados seleccionados.
En el muestreo aleatorio estratificado las unidades muéstrales son los elementos individuales de la población, mientras que en el muestreo por conglomerados las unidades muéstrales son conglomerados de elementos.
El tamaño de muestra, cuando se utiliza muestreo por conglomerados, equivale a escoger el número m de conglomerados de elementos de una población de M conglomerados.
Es importante recalcar que, en el muestreo por conglomerados, se puede incrementar la información obtenida de la población, seleccionando un mayor número de conglomerados de menor tamaño. La excepción a esta regla es el caso en que la población consiste en muchos grupos homogéneos pequeños. Los conglomerados deben ser heterogéneos dentro de sí.
En algunos casos utilizándo un mayor número de conglomerados pequeños en lugar de unos cuantos conglomerados grandes.
3.1. Estimación de la media poblacional. (m)
Varianza estimada del estimador.
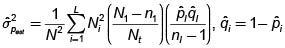
Donde:
número de elementos del i-ésimo conglomerado
: total de las mediciones del conglomerado i
Varianza estimada del estimador.
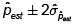
Intervalo de confianza para estimar m
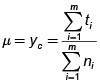
M es el número de conglomerados en la población y m es el número de conglomerados en la muestra.
3.2. Estimación del total poblacional (T)
Estimación.
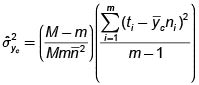
Varianza estimada del estimador.
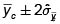
Intervalo de confianza para estimar T.
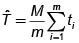
3.3 Estimación de la proporción poblacional (p)
Estimador.
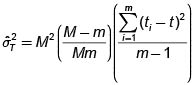
Varianza estimada del estimador.
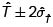
4. Muestreo por conglomerados bietápico
El muestreo por conglomerados bietápico se utiliza:
• Cuando un conglomerado contiene demasiados elementos para obtener una medición de cada uno de ellos,
• Cuando los elementos de un conglomerado son tan semejantes que la medición de sólo irnos cuantos proporciona información sobre el conglomerado completo.
Cuando ocurre alguna de estas situaciones el experimentador puede seleccionar una muestra aleatoria de conglomerados y después tomar una muestra aleatoria de los elementos dentro de cada conglomerado.
Por ejemplo, puede realizarse con propósitos de control de calidad. Así, el inspector comúnmente muestrea cajas y después muestrea paquetes dentro de cajas. También, cuando se están muestreando artículos producidos en diversas etapas de proceso, uno podría muestrear etapas del proceso y posteriormente muestrear artículos producidos en cada etapa muestreada.
Existen dos condiciones para seleccionar una muestra por conglomerados en dos etapas.
1. Proximidad geográfica de los elementos dentro de un conglomerado, y
2. Tamaños de conglomerado convenientes para su manejo.
Para seleccionar una muestra,
1. Se obtiene un marco muestral que liste todos los conglomerados en la población.
2. Se selecciona una muestra aleatoria de conglomerados aplicando M.A.S.,
3. Se obtienen marcos muéstrales que listen todas las unidades de cada uno de los conglomerados seleccionados, y
4. Se selecciona una muestra aleatoria de los elementos de cada uno de estos marcos muéstrales.
5. Muestreo poliétapico
El muestreo por conglomerados bietápico puede extenderse a un muestreo de tres etapas, cuatro etapas,...o muestreo poüetápico.
Por ejemplo, las agencias que efectúan encuestas de opinión pública pueden disponer de un listado de las universidades de un país, donde cada uno de éstas se constituye en un conglomerado. Se selecciona una muestra de universidades, las cuales a su vez están conformados por facultades. Posteriormente se selecciona una muestra facultades de cada una de las universidades seleccionadas anteriormente. Luego se selecciona una muestra de estudiantes de cada facultad seleccionada que serían los elementos muéstrales a empadronar.
El Muestreo por áreas es un caso especial del muestreo por conglomerados, en el cual la población es dividida por áreas geográficas. Luego se selecciona una muestra de estas áreas en forma aleatoria y posteriormente se realiza un muestreo o un censo, para determinar los elementos de cada área elegida que serán encuestados.
Este muestreo es muy utilizado puesto que no requiere de un marco muestral que identifique los elementos que conforman la población.
6. Muestro sistemático
Este método facilita la selección de la muestra puesto que es más fácil de ejecutar y menos costoso que el M.A.S.
Suponga que N unidades en la población se enumeran de 1 a N en algún orden.
Para seleccionar una muestra de n unidades se procede de la siguiente manera:
• Determinar el intervalo muestral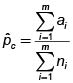
Por ejemplo; si se tiene una comunidad de 10.000 miembros y de éstos se seleccionan 200, el intervalo muestral sería
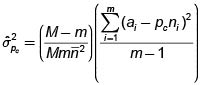
• Se escoge un número al azar entre 01 a 50 y si este número es por ejemplo igual a 12, la muestra estaría constituida por los miembros: 12,62,112,...
No es recomendable cuando los datos tienen un comportamiento cíclico y cuando no se conoce el tamaño de la población.
Muestreos no probabilísticos
1. Muestreo por conveniencia
Es aquel con el cual se seleccionan las unidades muéstrales de acuerdo a la conveniencia o accesibilidad del investigador.
Este muestreo se puede utilizar en los casos en que se desea obtener información de la población, de manera rápida y económica. Las muestras por conveniencia se pueden utilizar en las etapas exploratorias de la investigación como base para generar hipótesis y para estudios concluyentes en los cuales el investigador desea aceptar el riesgo de que los resultados del estudio tengan grandes inexactitudes.
Este método es muy común en las entrevistas callejeras como solicitar la opinión de las personas que trnasitan en un centro comercial, realizar entrevistas con personas de la calle para un canal de televisión, utilizar grupos de estudiantes o grupos religiosos para realizar un experimento, etc. En cada caso la unidad o elemento de muestreo se autoselecciona o se ha seleccionado con base en su fácil disponibilidad. En ninguno de los casos se especifica claramente la población del a cual se ha tomado la muestra real. Aún más, se desconoce la probabilidad exacta de que estas personas sean seleccionadas.
Este método de muestreo no se recomienda para estudios concuyentes, descriptivos, ni experimentales.
2. Muestreo según criterio (juicio)
Con este método la selección de los elementos de la muestra se realiza de acuerdo con el juicio y criterio del investigador.
Por ejemplo, en una investigación sobre las ventas diarias de todos los supermercados de una ciudad, el investigador, a juicio, selecciona primero aquellos supermercados que son más re presentativos.
3. Muestreo por cuotas
Las muestras por cuotas son un tipo especial de muestras a propósito.
En este caso el investigador da pasos concretoscon el fin de obtener una muestra que es similar a la población en algunas aracterísticas de "control", anteriormente especificadas.
El investigador dtermina el númeor de entrevistados, y lso entrevistadores eligen a sus entrevistados libremente con base en sus conocimientos y experiencia.
Bibliografía
Cochran, Willian G. Técnicas de Muestreo. Editorial Continental S.A. México, 1972.
Fowler, Newton Enrique. El muestreo Estadístico Aplicado a la Auditoría. Editorial Macchi. Buenos Aires, 1972.
III Simposio de Estadística. Muestreo. Universidad Nacional de Colombia, 1992
Kimmear, Thomas c; Taylor, James R. Investigación de Mercados. Editorial McGraw Hill, Colombia, 1999
- Kish,Leslie. Muestreo de Encuestas. Editorial Trillas, México, 1972.
- Scheaffer, Richard L. Mendenhall, Willian; Ott, Lyman. Elementos de Muestreo. Editorial Grupo Editorial Iberoamérica, México, 1986.