ARTÍCULOS
OBTENCIÓN DE GRÁFICAS ALTERNATIVAS PARA FACILITAR EL USO DE LOS RESULTADOS DE UNA REGRESIÓN DE COX
José D. Bermudez*
*Documento Internet Explorer. Hospital de Sagunto.
El objeto de este informe es mostrar cómo se pueden construir dos tipos de gráficas que pueden resultar muy útiles. La primera, es una gráfica que relaciona el índice pronóstico (resultado de la ecuación de las covariables seleccionadas en el modelo con sus correspondientes coeficientes) con la probabilidad de sobrevivir a un tiempo dado. La segunda, muestra la relación entre el índice pronóstico y la mediana de supervivencia (esto es, el valor del tiempo t para el que un individuo con índice pronóstico x presenta una supervivencia del 50%).
En él se muestra como se pueden construir esos dos tipos de gráficas, utilizando los datos Mieloma. Múltiple.
Como índice pronóstico, x, vamos a considerar la combinación lineal de covariables, utilizando los coeficientes propuestos por la regresión de Cox.
De esta forma simplificamos el cálculo del índice, pues no hará falla emplear la función exponencial.
Para la construcción de las dos gráficas es necesario conocer la función de supervivencia base, S0(t), o cualquier equivalente suyo: función de azar acumulado, función de densidad, función log menos log, etc.
El SPSS no nos muestra una tabla de la función de supervivencia (sí podríamos ver su gráfica y a partir de ella, construir la tabla nosotros mismos). pero sí nos muestra una tabla de la función de azar acumulado base, h0(t), así que vamos a hacer todos los cálculos a partir de esa función.
Una vez leídos los datos de Mieloma Múltiple:
Estadística
– Supervivencia
– Regresión de Cox
Tiempo: meses
Status: censura (0) Covanables : logbun y hb Opciones: Ver función de línea base.
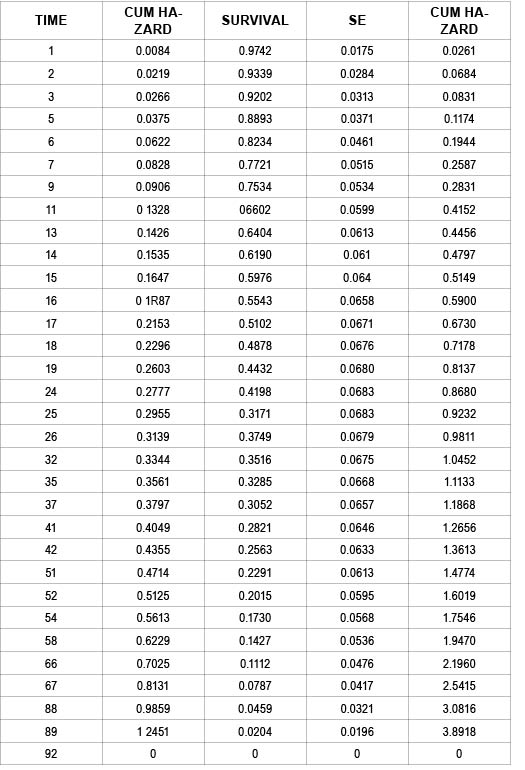
Al ejecutarlo obtendremos, entre otros resultados, la siguiente tabla:
Todo lo que necesitamos son las dos primeras columnas: la primera es el tiempo, t, y la segunda la función de azar acumulado base, h0(t), las demás columnas tienen que ver con un individuo con valores medios de covariantes, y no las vamos a necesitar para nada.
La función h0(t) es escalonada (como todas las gráficas tipo Kaplan Meier), así que su valor para un tiempo t que no aparezca en la tabla, coincide con el del tiempo más cercano e inferior a t que aparezca en tablas. Por ejemplo, para t = 10 esa función vale 0.0906.
Vamos a guardar esta tabla (solo las lineas de número sin el encabezamiento), copiando y pegando, en un documento solo texto que llamaremos "tabla.dar".
Gráfica 1: Relación entre índice pronóstico y la supervivencia a un tiempo fijo.
Vamos a dibujar en la misma gráfica tres curvas: una para 10 meses, otra para 40 meses y la última para 60 meses. (De la misma forma se dibujarían cualquier número de gráficas).
Los valores de la función de azar acumulado base para esos tres tiempos, obtenidos a partir de la tabla, son: 0.0906, 0.3797 y 0.6229 respectivamente.
Paso 1
Abrir un nuevo banco de datos en SPSS y crear una primera columna.
Esta columna debe tener tantos datos como puntos deseemos utilizar para el cálculo de la gráfica. Con 100 puntos suele ser ya bastante, pero si queremos más calidad en el dibujo puede que necesitemos 200 o incluso 500 puntos Aquí vamos a utilizar 100 puntos.
No necesitamos los datos de esta columna para nada más, por lo que copiando y pagando podemos hacerla tan larga como queramos con poco esfuerzo.
Paso 2.
Crear la columna de valores de los índices pronóstico que vamos a representar.
Para ello hemos de decidir los índices mínimo y máximo a representar. Aquí vamos a representar desde x=–2.5 hasta x=3.5 (En general, vale la pena dibujar primero un rango de índices muy grande para, a la vista de gráfica resultante, decidir qué rango de valores es el más adecuado).
Transformar --> Calcular
Variable de destino: índice = ($casenum-1)/100 * 6–2.5
(100 es el número de puntos a utilizar, que coincide con el número de datos introducido en el Paso 1.6 es la distancia del x mínimo al máximo y –2.5 es el mínimo. $casenum es una variable interna del SPSS que representa el número de individuos en el banco de datos).
Paso 3
Calcular los valores de las tres curvas a representar.
Transformar --> Calcular
Variable de destino: t1=exp(–0.0906* exp(índice))
De forma similar se calculan las otras dos curvas, tan solo sustituir 0.2832 (valor de la función de azar acumulado para 10 meses) por los correspondientes valores para 40 y 60 meses:
Transformar --> Calcular
Variable de destino: t2 =exp(–0.3797 * (índice))
Transformar --> Calcular
Variable de destino : t3 = exp(–0.6229 * exp(índice))
Paso 4
Dibujar las curvas
Gráficas --> Dispersión
Superposición
Pares Y–X: t1-índice, t2-índice, t3-índice
Editar la gráfica --> Atributos
interpolación
Recto Marcadores: punto "."
Luego, modificar los ejes para seleccionar la parte del plano a dibujar y modificar la leyenda.
El resultado final es la gráfica:
Paso 1
Leer tabla de azar acumulado base. Tabla que hablamos guardado en el fichero tabla.dat". con formato "solo texto"
Archivo --> Leer datos ASCII
Formato de archivo : Libre
Nombre del archivo : tabla.dat
Variables definidas: t.h.v1.v2.v3.
Paso 2
Construir los valores de los índices pronósticos asociados a la función mediana.
Transformar --> Calcular
Variable de destino: x= In (In (2) / h))
Paso 3
Dibujar la función.
Gráficas --> Dispersión
Simple Eje Y:t Eje X:x
Editar la gráfica --> Atributos
Interpolación: Salto a la derecha
Marcadores: punto "."
Luego, modificar los ejes para seleccionar la parte del plano a dibujar, y modificar la leyenda.
El resultado final es la gráfica