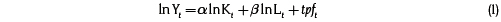
ARTÍCULOS

PRODUCTIVIDAD TOTAL DE LOS FACTORES, CAMBIO TÉCNICO, EFICIENCIA TÉCNICA Y PIB POTENCIAL EN LATINOAMÉRICA^*

TOTAL FACTOR PRODUCTIVITY, TECHNICAL CHANGE, TECHNICAL EFFICIENCY AND POTENTIAL GDP IN LATIN AMERICA

PRODUTIVIDADE TOTAL DOS FATORES, MUDANÇA TÉCNICA, EFICIÊNCIA TÉCNICA E PIB POTENCIAL NA AMÉRICA LATINA

Jhon Alexander Méndez Sayago^**; Johanna Mildred Méndez Sayago^***; Hugo Alfonso Hernández Escolar^****

** Ingeniero Civil, Universidad Francisco de Paula Santander, Cúcuta, Colombia. Magíster en Economía del Medio Ambiente y de los Recursos Naturales, Universidad de los Andes, Bogotá, Colombia. Magíster en Economía, Universidad Javeriana, Bogotá, Colombia. Profesor asistente de la Facultad de Ciencias Sociales y Económicas de la Universidad del Valle, Cali, Colombia. Miembro del grupo de investigación en Economía Regional y Ambiental (GERA), Universidad del Valle, Cali, Colombia. Correo electrónico: jhon.mendez@correounivalle.edu.co.

*** Ingeniera de Producción Industrial, Universidad Francisco de Paula Santander, Cúcuta, Colombia. Magíster en Economía, Universidad Javeriana, Bogotá, Colombia. Profesora de la Facultad de Estudios a Distancia, Universidad EAN, Bogotá, Colombia. Correo electrónico: jmmendez@correo.ean.edu.co.

**** Economista, Universidad Nacional, Bogotá, Colombia. Magíster en Economía, Universidad Javeriana, Bogotá, Colombia. Profesor de la Facultad de Ciencias Económicas y Contables, Fundación Universitaria Los Libertadores, Bogotá, Colombia. Correo electrónico: hahernandeze@hotmail.com.

Recibido: 02 de octubre de 2012
Aceptado: 20 de octubre de 2013

RESUMEN

PALABRAS CLAVE

CLASIFICACIÓN JEL

CONTENIDO

ABSTRACT

KEY WORDS

JEL CLASSIFICATION

CONTENT

RESUMO

PALAVRAS CHAVE

CLASIFICAÇÃO JEL

CONTEUDO

Introdução; 1. Produtividade total dos fatores; 2. Eficiência técnica; 3. Fronteira de produção paramétrica determinística e estocástica; 4. Mudança técnica e eficiência técnica variável no tempo; 5. Dados; 6. Resultados; 7. Conclusões; Bibliografia; Anexos.

INTRODUCCIÓN

El concepto de productividad total de los factores (PTF) ha conservado su vigencia como objeto de estudio y medición desde su incorporación en la literatura sobre crecimiento económico, gracias a su difusión en el artículo pionero de Solow (1957) sobre el cambio tecnológico y la función de producción agregada. Según Bernal (2010), la contribución de Solow (1957) fue cuantificar las variaciones de la producción debidas al progreso técnico en forma residual, razón por la cual al progreso técnico se lo conoce también como residuo de Solow o PTF.

De acuerdo con Castro, Perilla y Gracia (2006, p. 1):

La PTF es la contribución al producto que no está explicada por los cambios en la inversión (entendido como acumulación de capital) o el empleo, razón por la cual la productividad se mide como un residuo. Este residuo que se considera por muchos como una ''medida de nuestra ignorancia'', es un concepto sobre el cual es posible tejer variadas hipótesis sobre sus determinantes y la manera en que opera y se traduce en mayor o menor producto.

A pesar de sus limitaciones por ser solo un enfoque contable de las fuentes de crecimiento, el residuo de Solow es una herramienta fundamental para entender el crecimiento de los países, por tratarse de una potente aproximación empírica al desarrollo de sus principales determinantes. Al respecto, Bernal (2010, p. 347) argumenta que

[...] hoy existe consenso sobre la importancia de la productividad como fuente de crecimiento. Los estudios de Prescott (1998) apoyan esta posición y argumentan que el estudio de esta variable es aún muy precario a pesar de su importancia, pues explica más del 80 % del crecimiento económico en los países desarrollados y cerca del 40 % en los del Tercer Mundo.

Las estimaciones tradicionales de la contribución de la PTF al crecimiento económico presentan cambios bruscos. Por ejemplo, el ejercicio de Solow (1957) para los Estados Unidos muestra que en 1910 su contribución era del 156 %; en 1926, del 304%, y en 1927 y 1928, del -191 % y el -180 %, respectivamente.

Con respecto a América Latina, Solimano y Soto (2005) realizan un análisis de las fuentes del crecimiento para identificar el proceso de desarrollo de esta región, y concluyen que el deterioro del producto interno bruto en las últimas décadas del siglo pasado, tiene como causa principal una caída de la PTF. El estudio identifica los determinantes de la PTF que pueden estar detrás de la caída del crecimiento: el ciclo de negocios, la calidad de la fuerza del trabajo, los impactos (shocks) externos y la inestabilidad macroeconómica.

Loayza, Fajnzylber y Calderón (2005) para un subconjunto de países de la misma región, encuentran crecimiento positivo de la PTF entre los años 1960 y 1980, crecimiento negativo en promedio, entre 1980 y 1990, y otra vez crecimiento positivo en promedio, entre 1990 y 2000. Bernal (2010) se pregunta sobre el origen de estos cambios bruscos y, en general, cuestiona la validez del cálculo de la PTF tal como la planteó Solow (1957), ya que de acuerdo con la teoría evolucionista, estos cambios de signo no serían posibles, pues los agentes no olvidan, no desaprenden; por el contrario, existe una mejora continua.

A pesar de la incorporación de distintas técnicas econométricas, en las últimas décadas se ha mantenido la forma de cálculo de la PTF, como el residuo obtenido después de la estimación de una función de producción neoclásica; eso quiere decir, una función donde se conjetura competencia perfecta, ausencia de capacidad ociosa, además de que los factores productivos se remuneran conforme a sus productividades marginales, lo que implica que están debidamente utilizados, razón por la cual no hay ineficiencias.

Por lo tanto, es conveniente desarrollar un análisis de productividad que además de tener en cuenta la heterogeneidad presente entre los distintos países de Latinoamérica, también incorpore la probable existencia de ineficiencias técnicas en la producción, que inciden en la estimación de la PTF, para lograr determinar cuál sería el PIB potencial de estos países si operaran sobre la frontera de producción, y si las ineficiencias son la causa o están relacionadas con los cambios observados en el crecimiento de la PTF.

Soltelsek y Laborda (2010) abordaron este problema al calcular el crecimiento de la PTF experimentado por las economías latinoamericanas entre 1980 y 2004, mediante el cálculo del índice de Malmquist, combinado con la utilización del análisis envolvente de datos (DEA), una técnica no paramétrica utilizada para medir la productividad, y desagregaron las mejoras de eficiencia y de cambio técnico por país.

La técnica DEA tiene, sobre la estimación paramétrica, la ventaja de su flexibilidad, ya que su análisis de eficiencia no está basado en conocimiento de la función de producción, porque obtiene la envolvente o frontera de unidades eficientes a partir de combinaciones lineales de las mismas. También puede incorporar economías de escala, un factor importante que puede justificar su elección. Sin embargo, según Sanhueza (2003), el principal inconveniente de la técnica DEA es la falta de propiedades estadísticas de los resultados obtenidos mediante la programación lineal.

Este artículo utiliza las técnicas paramétricas de datos panel de efectos fijos y el análisis de frontera estocástica para el cálculo de la eficiencia técnica y la estimación del cambio técnico en 18 países de América Latina, durante un período comprendido entre los años 1980 y 2009. El análisis determinó el incremento del progreso técnico en la mayoría de los países y una ligera caída de la eficiencia técnica que, sin embargo, no logra explicar los cambios bruscos en la PTF sobre los cuales se cuestiona Bernal (2010).

El artículo está organizado de la siguiente forma: en el capítulo 1 se presenta la descomposición de la PTF de acuerdo con la metodología asumida. En el capítulo 2 se discute el uso de la medida de eficiencia técnica como parámetro de desempeño de las unidades productivas. En el capítulo 3 se hace una ligera introducción al análisis de frontera determinística y estocástica. En el capítulo 4 se presentan los procedimientos a utilizar en el cálculo de la eficiencia técnica. En el capítulo 5 se explican los datos para, a continuación, en el capítulo 6, presentar los resultados, y por último, presentar las conclusiones.

1. PRODUCTIVIDAD TOTAL DE LOS FACTORES

Según el modelo de crecimiento de Solow (1956), una economía se caracteriza por la dotación de factores productivos como el capital y el trabajo, y por la forma en que estos se combinan de acuerdo con una estructura tecnológica determinada. En su expresión más simple, el comportamiento de la economía podría caracterizarse mediante una función de producción tipo Cobb Douglas:

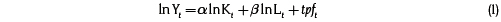
Donde Y_t, K_t, L_t y tpf_t representan, respectivamente, el PIB real, el valor real del acervo de capital, el nivel de empleo y el logaritmo de la productividad total de los factores (residuo de Solow), observados en el momento t. Los parámetros de la función de producción (las elasticidades α y β) son desconocidos y deben estimarse. Como menciona Acevedo (2009) una alternativa para su estimación es suponer que la función de producción tiene rendimientos constantes a escala (es decir ) α + β = 1) y que existe competencia perfecta. Así α y β podrían obtenerse de forma directa de las cuentas nacionales, ya que representarían la participación del trabajo y del capital en el ingreso nacional, respectivamente.

En este artículo se adopta una estrategia alternativa, que consiste en la estimación econométrica de los parámetros de la función de producción. Después, se sustituyen los valores de α y β estimados en la ecuación (1), para obtener mediante una simple resta, la productividad total de los factores:

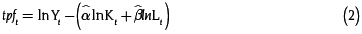
A diferencia de este análisis tradicional, en este artículo la diferencia (2) es considerada un residuo :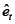

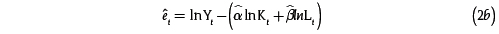
Este residuo tiene dos componentes:

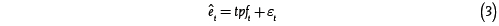
Donde _t es ruido blanco, agrupa el efecto de otros factores sobre el PIB real y que no son considerados en la función de producción, pero no tienen un efecto sistemático sobre el producto.

Por otra parte, la tpf puede descomponerse en dos factores que afectan el PIB real:

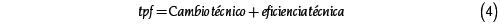
El primer componente, el cambio técnico, puede ser modelado como una función f(t) que depende del tiempo. El segundo componente es la eficiencia técnica, que se puede obtener a partir de la estimación econométrica de fronteras determinísticas o estocásticas. Ambas especificaciones econométricas son utilizadas en este artículo para estimar la frontera de producción.

2. EFICIENCIA TÉCNICA

La eficiencia productiva se refiere a la utilización más adecuada de los recursos disponibles, dada la tecnología existente en el momento. Este desempeño de las unidades de producción se puede medir de varias formas. Una medida natural es la razón de la productividad, que se define como la relación entre los productos de una firma y los insumos que utiliza para obtenerlos:

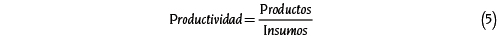
Valores más altos de esta relación están asociados a un mejor desempeño de las firmas. El problema es que la productividad no es una buena medida del desempeño de las unidades productivas, porque la productividad media está afectada por la evolución de la productividad marginal. Por ejemplo, en el gráfico 1, los puntos A y C son eficientes (están sobre la frontera de producción) mientras que B no es eficiente, sin embargo, la productividad en B es mayor que en C, porque esa medida no tiene en cuenta los rendimientos marginales decrecientes.

La eficiencia técnica se define como la habilidad de obtener el máximo producto, dados unos insumos y una tecnología fija (habilidad de usar la menor cantidad de insumos para obtener una cantidad dada de producto). Las firmas que operan en la frontera de producción son técnicamente eficientes.

Las medidas de eficiencia técnica, en el análisis de frontera determinística o estocástica, están inspiradas en las propuestas de Debreu (1951) y Farrell (1957).

La medida de eficiencia técnica Debreu-Farrell se define como la máxima contracción equi-proporcional en todos los insumos, que permite continuar con la producción, dado el vector de insumos. Es una medida de carácter radial. Si no es posible contraer de forma equi-proporcional todos los insumos, se dice que el vector de insumos es técnicamente eficiente.

Con múltiples insumos y un solo producto, como es el enfoque de análisis de eficiencia que se adopta en este artículo, la eficiencia técnica ET(x^A, y^A) mide la máxima expansión de y^A (la producción del bien y de la unidad productiva A) que es posible con la combinación de insumos x^A. Para medir ET(x^A, y^A) se compara la producción del par de isocuantas en el gráfico 2:

Es decir, la firma A podría producir 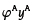, con 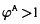, pero solo produce y^A, con lo que la eficiencia técnica puede ser calculada así:

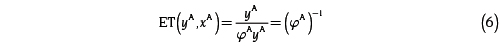
Como 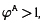entonces 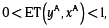y para las unidades de producción eficientes,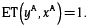

3. FRONTERA DE PRODUCCIÓN PARAMÉTRICA: DETERMINÍSTICA Y ESTOCÁSTICA

La frontera de producción para el cálculo de la eficiencia técnica puede obtenerse a través de técnicas paramétricas y no paramétricas. Los métodos paramétricos estiman la función de producción a través de procedimientos econométricos y los no paramétricos construyen la frontera mediante métodos de programación lineal.

Las técnicas no paramétricas como el análisis envolvente de datos tienen la ventaja de la flexibilidad, porque no es necesario suponer una forma funcional para establecer la relación entre insumos y productos. La principal ventaja de los métodos paramétricos es que son modelos econométricos y por tanto los estimadores obtenidos para la ineficiencia tienen propiedades estadísticas conocidas. Sin embargo, ya que no hay justificación teórica que valide la especificación de una determinada forma funcional, su principal inconveniente, es que posibles errores en la especificación pueden confundirse con la ineficiencia técnica.

La estimación paramétrica de las fronteras de producción se divide en determinística y estocástica.

En los modelos de frontera determinística, a las desviaciones del producto con respecto a la frontera se les considera ineficiencia técnica, y esta se mide mediante la relación que hay entre el producto (output) observado, y el máximo nivel posible permitido por la función de producción.

Los modelos de frontera estocástica de producción son introducidos en la literatura por Aigner, Lovell y Schmidt (1977) y Meeusen y van den Broeck (1977).

Se parte de la especificación de una frontera de producción, en la que se suponen N inputs utilizados para producir un output simple, disponibles para cada productor de un conjunto de I productores:

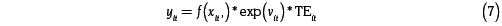
En la expresión (7), el producto 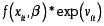corresponde a la especificación de una frontera de producción estocástica, donde y_it es el output de la unidad de producción i en el momento t, x es el vector de insumos, β los parámetros de la función de producción, y exp(v_it) es la parte específica al productor que captura el efecto de un shock aleatorio en el momento t sobre el productor i. La especificación de la ecuación (7) permite que la diferencia entre el nivel de producto observado y el máximo factible no sea atribuida solo a la ineficiencia técnica. Esta especificación considera que el output puede ser afectado por choques aleatorios, los cuales no están bajo el control del productor.

De acuerdo con la especificación, la eficiencia técnica del productor i en el momento t se puede calcular como:

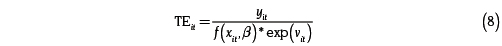
Es decir, se define la eficiencia técnica como la razón entre el output observado y el máximo factible en un ambiente caracterizado por choques. La gran virtud de estos modelos es que el impacto sobre el producto de un choque de trabajo o desempeño de la maquinaria, etc., puede ser, en principio, separado de la contribución de variaciones en eficiencia técnica.

4. CAMBIO TÉCNICO Y EFICIENCIA TÉCNICA VARIABLE EN EL TIEMPO

La eficiencia técnica cambiante en el tiempo, se refiere al acercamiento o distanciamiento del nivel de producción de una unidad productiva, con respecto a la frontera de posibilidades de producción del sector o la industria a la que pertenece, a diferencia del cambio técnico, que está asociado al desplazamiento de la frontera de posibilidades de producción.

Si se dispone de información de datos panel que involucre varios períodos, es posible que se presente cambio técnico, así como también, que la eficiencia técnica cambie con el tiempo.

Si se especifica una función de producción Cobb-Douglas, la frontera estocástica con eficiencia técnica cambiante en el tiempo puede escribirse de la siguiente forma:

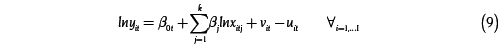
Donde:

u_it es el término asociado a la ineficiencia técnica (cambiante en el tiempo),

v_it es el error aleatorio, y

β_0tel intercepto común a todos los productores en el período t.

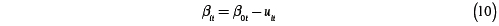
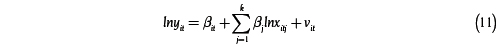
La existencia del parámetro α_it implica un intercepto diferente para cada firma en cada momento del tiempo. La estimación del modelo implica utilizar T * 1 variables binarias para modelar todos los interceptos:

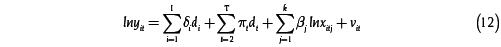
Sin embargo, como el número de coeficientes a estimar T * 1 + k es mayor que la información disponible T * I observaciones, la estimación no es posible.

Como solución al problema, Cornwell, Schmidt y Sickles (1990) proponen como estrategia alternativa estimar el modelo (11), con β_it como una función del tiempo:

Donde el número de coeficientes a estimar es 3 * I + k, que puede ser mucho menor que la información disponible T * I observaciones, si la serie de tiempo T es grande.

4.1. Estrategia de estimación por efectos fijos

Los pasos de la estrategia de estimación por el método de efectos fijos son los siguientes:

1. Estimar la ecuación: 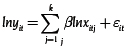con la técnica de efectos fijos de datos panel y obtener los residuales .

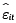2. Realizar la regresión de 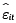sobrel, t,t² 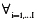para obtener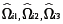

3. Calcular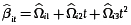

4. Determinar el valor de la frontera para cada período de tiempo .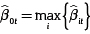

5. Encontrar el componente de ineficiencia técnica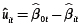

6. Encontrar el índice de eficiencia técnica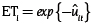

4.2. Estimación por máxima verosimilitud

Es posible realizar la estimación por máxima verosimilitud, bajo algunos supuestos sobre el comportamiento de u_it y v_it en la ecuación (9), en particular:

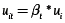
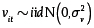
Batesse y Coelli (1992) asumen una forma funcional específica para el coeficiente α_t que solo requiere la estimación de un parámetro γ:

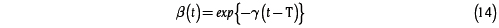
Esta función tiene las siguientes características:

i. β(t)0

ii. β(t) decae si γ>0, crece si γ<0 o permanece constante si γ=0

En este artículo el intercepto cambiante en el tiempo, o cambio técnico, es modelado como:

Es decir, se asume que no existe heterogeneidad en el cambio técnico, para ser coherente con la especificación de Batesse y Coelli (1992).

5. DATOS

Para la estimación de la frontera de producción estocástica, con las aproximaciones de Cornwell, Schmidt y Sickles (1990) y Batesse y Coelli (1992), se utilizó información de datos panel para el período 1980-2009 del PIB real, el acervo de capital y el empleo de 18 países latinoamericanos: Argentina, Bolivia, Brasil, Chile, Colombia, Costa Rica, Guatemala, República Dominicana, Ecuador, Honduras, México, Nicaragua, Salvador, Panamá, Paraguay, Perú, Uruguay, Venezuela. Por consiguiente, la eficiencia técnica, la productividad total de los factores y el PIB potencial se estimaron para este período de tiempo y para estos países.

La información sobre el PIB real tiene como fuente las estadísticas del Banco Mundial, así como la información de la mano de obra total. El acervo de capital, se calculó mediante el método del inventario perpetuo:

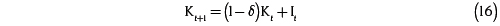
Con una tasa de depreciación de 4 % anual. Para I_t se utilizó la formación bruta de capital fijo, también proveniente de las estadísticas del Banco Mundial. Para el cálculo del capital inicial se utilizó la metodología descrita en Harberger (1969).

6. RESULTADOS

El primer paso consistió en la estimación de la función de producción con la técnica de efectos fijos para datos panel. Los resultados se muestran en la tabla 1.

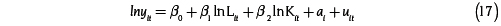
Los resultados de la tabla 1 revelan que tanto el acervo de capital como el trabajo son variables significativas con niveles de significancia α hasta del 1 %. El modelo de la ecuación (17) fue transformado para probar la hipótesis de rendimientos constantes a escala.

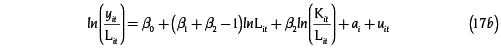
Los resultados de la estimación de la ecuación (17b) se muestran en la tabla 2. Se puede observar que se acepta la H_o de que el coeficiente de la variable trabajo es igual a cero, porque su Pvalor = 0.513 > α, con α = 5% o α = 10% o, lo que es lo mismo, se acepta la hipótesis β₁ + β₂ = 1, así que se concluye que la función de producción presenta rendimientos constantes a escala.

Para la estimación del cambio técnico, con la metodología de Cornwell, Schmidt y Sickles (1990), se calcula el componente :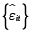

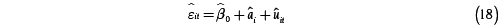
Los resultados de la regresión de 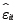sobre l, t, t² 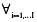para obtener 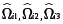se muestran en la tabla 3. Se puede observar que para cualquier nivel de significancia α pequeño, se rechaza las hipótesis nulas 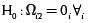y 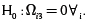La estimación también se realizó por efectos fijos, para encontrar 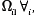que es el resultado del intercepto reportado en el modelo más el efecto fijo.

La tabla 4 presenta los resultados de la estimación del cambio técnico según la metodología de Batesse y Coelli (1992). No se estima la función de producción, solo la función del cambio técnico homogénea. Se puede observar que para cualquier nivel de significancia α pequeño, se rechazan las hipótesis nulas 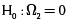y 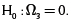También se rechaza la hipótesis nula 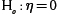Pvalor = 0,513 > α = 5%, así que se demuestra que la eficiencia técnica es variable, cae con el tiempo.

El anexo A muestra los gráficos del índice de eficiencia técnica variable a través del tiempo para los 18 países, estimados con frontera estocástica y la técnica de datos panel y efectos fijos. En la eficiencia técnica calculada a partir del método de Batesse y Coelli (1992), todos los países sufren una leve disminución de la eficiencia técnica con el pasar de los años. Los cálculos a partir del método de Cornwell (Schmidt y Sickles, 1990) reportan mejoras en la eficiencia técnica a través del tiempo en Argentina, Costa Rica, Ecuador, Bolivia, Chile y Uruguay, y una tendencia decreciente en el resto. Los mayores índices de eficiencia se encuentran en Panamá, Uruguay y México, y los más ineficientes son Nicaragua, Bolivia, Honduras y Paraguay. La situación de Nicaragua, Honduras y Paraguay es la más crítica, porque están entre los más ineficientes, y su ineficiencia empeoró en el tiempo.

Los anexos B y C muestran los aportes del capital 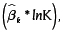el trabajo ( 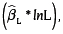la ptf, y otros factores al producto, así como el aporte técnico esperado (AT*) y el PIB real potencial que sucedería en el caso de que los países tuvieran un 100 % de eficiencia. El anexo B presenta estos resultados según la metodología de Cornwell, Schmidt y Sickles (1990), y el anexo C, para la metodología de Batesse y Coelli (1992).

Para mejor ilustración del contenido de los anexos 3 y 4, los gráficos 3, 4 y 5 presentan los resultados de la metodología de Cornwell, Schmidt y Sickles (1990) para Argentina:

• Del gráfico 3 se puede concluir que el aporte de la ptf al PIB real en Argentina es superior al aporte la mano de obra, lo que resalta la importancia de la productividad total de los factores al crecimiento económico.

• En el gráfico 4 se puede observar que en Argentina la brecha entre el aporte técnico esperado (PT) y la ptf se reduce a través del tiempo; esto, debido a que la eficiencia técnica en ese país ha mejorado. El aporte técnico esperado es la línea horizontal que se obtiene del valor calculado de la ptf del 1980 para Panamá (año y país con la mejor situación). La metodología estándar de Cornwell, Schmidt y Sickles (1990) recomienda calcular la frontera para cada período, pero como en esta investigación, el máximo valor se encuentra en el primer período, se prefirió conservar este valor como una única frontera.

• En el gráfico 5 se muestra la brecha el PIB potencial en Argentina, que resulta de sumar a la productividad total de los factores el aporte técnico esperado.

La tabla 5 presenta los resultados de la estimación de tendencia de largo plazo de la ptf calculada con la frontera estocástica. Se evidencia una tendencia de largo plazo creciente. Un comportamiento similar tiene la tendencia de largo plazo de la ptf calculada con la técnica de Cornwell, Schmidt y Sickles (1990).

El anexo D muestra la dinámica del progreso técnico y la eficiencia técnica, ambos calculados con la técnica de frontera estocástica. Se puede ver que el componente de progreso técnico es más alto que el de eficiencia técnica (aproximadamente cuatro veces más), por eso este componente domina la tendencia de largo plazo de la ptf.

7. CONCLUSIONES

El análisis de frontera ofrece la posibilidad de descomponer el residuo de Solow en tres elementos: el progreso técnico, la eficiencia técnica, y el aporte de otros factores al producto. La distinción entre eficiencia técnica y progreso técnico permite analizar mejor las causas de los cambios en la productividad total de los factores, y la adopción y aprovechamiento de la tecnología en los países.

La estimación de la función de producción para un conjunto de 18 países latinoamericanos arrojó como resultado que no se puede rechazar la hipótesis nula de rendimientos constantes a escala.

En general, para la muestra de datos anuales desde 1980 hasta 2009, puede concluirse una ligera caída en la eficiencia técnica en la productividad total de los factores para la mayoría de los países. Los países más eficientes son Panamá, Uruguay y México, y los más ineficientes son Nicaragua, Bolivia, Honduras y Paraguay.

La forma convexa de la función de progreso técnico, resultado de la estimación a través de frontera estocástica, o la de varios países en la estimación de la función de progreso técnico heterogéneo de la metodología de Cornwell, Schmidt y Sickles (1990), es comparable con los resultados de Loayza, Fajnzylber y Calderón (2002). Ellos encontraron en la década de 1980 caída en el aporte de la PTF al producto, y aporte positivo en la década de 1990 para la mayoría de países de Latinoamérica. Ese comportamiento solo puede ser captado por una función de progreso técnico convexa.

La brecha entre el progreso técnico y la productividad total de los factores se debe al aporte negativo de la ineficiencia técnica al PIB real. Aunque la magnitud de la ineficiencia técnica es creciente y no es despreciable, este componente no tiene un peso tan grande dentro en la productividad total de los factores, como para que pueda explicar los cambios de signo en la contribución de la productividad total de los factores al crecimiento económico observados por Loayza, Fajnzylber y Calderón (2005)

Una debilidad que tienen los resultados alcanzados en este artículo es la obtención del cambio técnico y la eficiencia técnica a través del método de Batesse y Coelli sin incorporar la función de producción. En su defecto se utilizó como variable dependiente el residuo de la estimación por mínimos cuadrados ordinarios de la función de producción con rendimientos constantes a escala. El problema es que la estimación directa de la función de producción, junto con el cambio técnico y la eficiencia técnica mediante máxima verosimilitud no tiene en cuenta los efectos fijos, y la estimación de las elasticidades de capital y trabajo resulta sesgada, hasta el punto de obtener valores incoherentes para estos parámetros. Por esta razón se acudió a la práctica desarrollada en este artículo.

También sería importante en las futuras investigaciones, cuando la información esté disponible, incorporar factores explicativos de la eficiencia técnica y el cambio técnico, que permitan no solo describir su comportamiento, sino tomar medidas de política tendientes a mejorar la productividad total de los factores.

Notas:

* Artículo de investigación producto del proyecto ''Productividad total de los factores, cambio técnico, eficiencia técnica y PIB potencial en latinoamérica''. Proyecto financiado con recursos aportados por La Universidad EAN, la Fundación Universitaria Los Libertadores y la Universidad del Valle.

¹ La frontera de producción define la relación entre productos e insumos. Representa el máximo producto que se puede obtener dados unos insumos. Refleja el estado actual de la tecnología en la industria.

² Se calcula con la expresión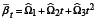

BIBLIOGRAFÍA

Acevedo, Ernesto (2009). PIB potencial y productividad total de los factores Recesiones y expansiones en México. En: Economía Mexicana Nueva Época, Vol. 18, N.° 2, pp. 175-219.

Aigner, D.; Lovell, C. y Schmidt, P. (1977). Formulation and estimation of stochastic frontier production function models. En: Journal of Econometrics, Vol. 6, N.° 1, pp. 21-37.

Battese, G. y Coelli, T. (1992). Frontier Production Functions, Technical Efficiency and Panel Data: With Application to Paddy Farmers in India. En: Journal of Productivity Analysis, Vol. 3, N.° 1, pp. 153-169.

Castro, C.; Perilla, J. y Gracia, O. (2006). El comercio internacional y la productividad total de los factores en Colombia. En: Archivos de Economía, N.° 307, Bogotá, DNP, 43 pp.

Cornwell, C.; Schmidt, P. y Sickles, R. C. (1990). Production frontiers with cross-sectional and time-series variation in efficiency levels. En: Journal of Econometrics, Vol. 46, N.° 1-2, pp. 185-200.

Debreu, Gerard (1951). The Coefficient of Resource Utilization. En: Econometrica, Vol.19, N.° 3, pp. 273-292.

Farrell, M. (1957). The Measurement of Productive Efficiency. En: Journal of the Royal Statistical Society, Series A (General), Vol. 120, N.° 3, pp. 253-290.

Harberger, A. (1969). La tasa de rendimiento del capital en Colombia. Departamento Nacional de Planeación. En: Revista de Planeación y Desarrollo, N.° 1, pp. 13-42.

Loayza, N.; Fajnzilber, P. y Calderon, C. (2005). Economic Growth in Latin America and the Caribbean: Stylized Facts, Explanations, and Forecasts. Banco Mundial, Washintong, marzo, 168 pp.

Meeusen W. y Van Den Broeck, J. (1977). Efficiency estimacion from Cobb-Douglas production functions with composed error. En: International Economic Review, Vol.18, N.° 2, pp. 435-444.

Prescott, C. (1998). Needed: A theory of total factor productivity. En: International Economic Review, Vol. 39, N.° 3, pp. 525-551.

Sanhueza (2003). Frontera de eficiencia: Metodología para la determinación del valor agregado de distribución. Tesis de Doctorado en Ciencias de la Ingeniería. Departamento de Ingeniería Electrónica, Escuela de Ingeniería, Pontificia Universidad Católica de Chile, 183p.

Solimano, A. y Soto, R. (2005). Economic growth in Latin America in the late 20th century: evidence and interpretation. En: Serie Macroeconomía del desarrollo, N.° 33 (LC/L.2236-P), Santiago de Chile, Comisión Económica para América Latina y el Caribe (CEPAL), Publicación de las Naciones Unidas, 44 pp.

Solow, Robert (1956). A Contribution to the Theory of Economic Growth. En: Quarlerly Journal of Economics, Vol. 30, N.° 1, pp. 65-94

Solow, Robert (1957). Technical change and the aggregate production function. En: The Review of Economics and Statistics, Vol.39, N.° 3, pp. 312-320.

Soltelsek, D. y Laborda, L. (2010). América Latina: medición de la eficiencia productiva y el cambio técnico incorporando factores ambientales. En: Revista de la CEPAL, N.° 101, pp. 17-37.

ANEXOS