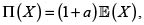 bajo el supuesto que
bajo el supuesto que 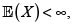 como es en nuestro caso, pues X es un riesgo. Para a = 0 se obtiene el conocido principio de prima neta.
como es en nuestro caso, pues X es un riesgo. Para a = 0 se obtiene el conocido principio de prima neta.ARTÍCULOS
Prima de la suma de dos riesgos dependientes PQD o NQD. Aplicación de algunas cópulas arquimedianas*
Premium of the sum from two risks dependent PQD or NQD - archimedean copulas application
César E. Escalante Coterio**; Carmen C. Sánchez Zuleta***
** MSc matemática. Empresas Públicas de Medellín. Gerencia Integral de Riesgos. Correo: cesar.escalante@epm.com.co.
** MSc. Matemáticas. Profesora investigadora, Universidad de Medellín. Correo: ccsanchez@udem.edu.co
Recibido:
11/02/2013
Aceptado: 27/06/2014
RESUMEN
En este artículo se estudia cómo se afecta la prima de la suma de dos riesgos X y Y con dependencia positiva PQD y dependencia negativa NQD con el uso de las cópulas como estructura general que gobierna tal dependencia. Se propone una demostración del Lema de Hoëffding y se usa para el cálculo de la varianza de X + Y. Se exponen y usan varios principios de prima (de varianza, de desviación estándar, de varianza modificada) y de medidas de dependencia más usadas (τ de Kendall, dependencia en la cola). Son presentados varios ejemplos numéricos de dependencia de riesgos con algunas cópulas arquimedianas.
PALABRAS CLAVE
dependencia de riesgos, cópulas arquimedianas, prima de riesgos dependientes, medidas de dependencia.
ABSTRACT
The premium of the sum of two risks X and Y with positive dependence PQD and NQD negative dependence and its impact is studied in this paper using copulas as the general structure that governs such dependence. We propose a demonstration of Hoeffding's lemma and is used to calculate the variance of X + Y. Various premium principles (variance, standard deviation, variance as amended) and most commonly used measures of dependence (τ of Kendall, dependence on the tail) are propoused and used. Several numerical examples risks of dependence with some Archimedean copulas are presented.
KEY WORDS
Risk-dependent, Archimedean copulas, dependent risk premium, measures of dependence.
INTRODUCCIÓN
En actuaría, para fijar el precio de un producto de seguros, tradicionalmente se ha trabajado con las hipótesis de la teoría clásica del riesgo que supone que las variables aleatorias (v.a.) de las cuantías individuales de los siniestros son independientes y tienen igual distribución (véanse las hipótesis del modelo de riesgo colectivo). La prima de riesgo se obtiene aplicando, además, el principio de mutualidad a partir del cual los riesgos se distribuyen entre toda la cartera asegurada, de forma que en promedio los errores se compensan y la esperanza matemática de la siniestralidad total, o prima pura, es suficiente para llevar a cabo la cobertura. Sin embargo, este procedimiento de determinación del precio del seguro es incongruente con la valoración realizada en los mercados financieros, en los que la cuantificación de los activos derivados se obtiene, evitando las oportunidades de arbitraje, mediante la réplica de carteras formadas por activos simples cuyos resultados son iguales, en todo momento del período de negociación al del activo derivado objeto de valoración.
En el presente artículo se estudia cómo se afecta la prima de dos riesgos, con dependencia positiva PQD o negativa NQD, usando algunos modelos de cópulas arquimedianas. A manera de ejemplo citamos algunas situaciones en las que se pueden presentar riesgos dependientes:
• El momento de la muerte de un hombre y su esposa debido a la exposición a riesgos similares, además de los posibles componentes emocionales.
• El valor indemnizado en un siniestro y el pago realizado por el asegurador al ajustador del siniestro.
• El pago total en diferentes líneas de negocio. Por ejemplo, una epidemia puede hacer que la línea de renta vitalicia sea más rentable que la línea de seguros de vida.
De forma resumida una prima mínima técnica está compuesta de los siguientes elementos:
• Prima pura de riesgo.
• Sobreprima de seguridad.
• Costo adicional para el beneficio.
Por tanto, la prima o precio del servicio es el costo que para la empresa suponen los siniestros, más el margen de beneficio. El precio correcto, llamado rating, es vital, pues si es demasiado bajo representa una pérdida para el asegurador, y si es demasiado alto se pierde competitividad.
Existen diversas definiciones de riesgo y no es fácil encontrar una que sirva en todas las disciplinas en que se usa este concepto. En este artículo se entiende por riesgo una v.a. no negativa con esperanza finita.
Existe gran variedad de fuentes para modelos bivariados y multivariados. Entre ellos están los libros de Hutchinson & Lai [1], Kotz, Balakrishnan & Johnson [2] y Mardia [3]; la mayoría de textos se enfocan en distribuciones multivariadas con distribuciones marginales del mismo tipo. De más interés y valor práctico son los métodos de construcción de modelos bivariados o multivariados a partir de distribuciones marginales conocidas (posiblemente diferentes) y de la dependencia entre riesgos. Hay muchas formas para describir la dependencia o asociación entre v. a. Por ejemplo, la medida clásica de dependencia es el coeficiente de correlación, que es una medida de la relación de linealidad entre v. a., y que toma los valores 1 o –1 cuando existe una relación lineal perfecta, esto es, cuando se puede escribir Y = aX + b para las v.a. X y Y, y constantes a y b. Si a es positiva, el coeficiente de correlación es 1; si a es negativa, el coeficiente de correlación es –1.
Esto explica por qué la correlación mencionada se llama a menudo correlación lineal. Otras medidas de dependencia entre v. a. son la tau de Kendall τK y ro de Spearman ρS. Similar al coeficiente de correlación, existen medidas de dependencia que toman el valor 1 para la dependencia positiva perfecta (no necesariamente lineal) y de –1 para la dependencia negativa perfecta.
1. PRINCIPIOS DE CÁLCULO DE PRIMA
En esta sección se presentan los principios de cálculo de prima más comunes. Primero se exponen algunas propiedades generales, no todas verificables de manera simultánea.
1.1 Algunas propiedades
Antes de presentar algunos de los principios de cálculo de prima de seguro más comunes discutimos las propiedades generales que hay detrás de la idea BUEN principio de cálculo de prima. La definición de riesgo propuesta conduce usualmente a que la prima Π(X), asociada a un riesgo X, sea finita, y en tal caso se dice que el riesgo X es asegurable. Sean X, Y, riesgos asegurables con funciones de distribución (fd) respectivas F y G. En Teugels et ál. [4] y Rolski et ál. [5] se listan, entre otras, las siguientes propiedades:
• Carga de seguridad. Para toda constante a > 0, Π(a) = a.
• Proporcionalidad. Para toda constante > 0, Π(aX) = aΠ(X).
• Consistencia. Para toda constante > 0, Π(X + a) = Π(X) + a.
• Subaditividad. Π(X + Y) ≤ Π(X) <(X) + Π(Y).
• Aditividad. Π(X + Y) Π(X) + Π(Y).
• Superaditividad. Π(X + Y) > Π(X) + Π(Y).
Por lo general, la propiedad de aditividad se exige para riesgos independientes, caso contrario al del objetivo central del presente trabajo. La subaditividad de un principio de prima significa que un asegurado no obtiene ventaja económica por dividir un riesgo en dos o más partes. En realidad la prima de seguros de dos riesgos depende de la distribución conjunta de X + Y, y por tanto centraremos la atención en ésta.
1.2 Principios básicos para el cálculo de primas
Uno de los principios más básicos para el cálculo de una prima es
• Principio de valor esperado. Para alguna constante a > 0, 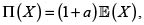 bajo el supuesto que
bajo el supuesto que 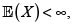 como es en nuestro caso, pues X es un riesgo. Para a = 0 se obtiene el conocido principio de prima neta.
como es en nuestro caso, pues X es un riesgo. Para a = 0 se obtiene el conocido principio de prima neta.
El principio de valor esperado parece justo, pero no tiene en cuenta la variabilidad del riesgo subyacente X, y esto puede ser peligroso para el asegurador. En un intento de superar este inconveniente, se introducen principios en los que la carga de seguridad 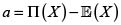 depende de la variabilidad de X. Por tanto, para alguna constante a > 0 tenemos los siguientes principios de prima:
depende de la variabilidad de X. Por tanto, para alguna constante a > 0 tenemos los siguientes principios de prima:
• Principio de varianza. 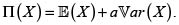 Se debe observar que este principio exige para su uso que las unidades en la que se expresa a sean iguales al recíproco de las unidades en la cual se expresa X.
Se debe observar que este principio exige para su uso que las unidades en la que se expresa a sean iguales al recíproco de las unidades en la cual se expresa X.
• Principio de desviación estándar.
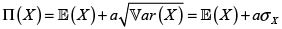
• Principio de varianza modificada. 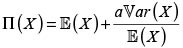 con
con 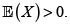
Realicemos el análisis básico de las propiedades de subaditividad, aditividad y superaditividad para la prima de la suma de dos riesgos posiblemente no independientes, con respecto a los principios de prima de varianza, desviación estándar y varianza modificada. Sea el riesgo X + Y, entonces:
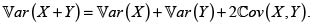
Prima del riesgo X + Y bajo el principio de varianza. Para a > 0,
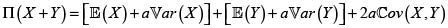
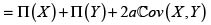
En consecuencia, si 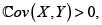 entonces
entonces 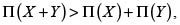 y por tanto, en este caso, el principio de varianza es superaditivo. De manera análoga, el principio de varianza es subaditivo si
y por tanto, en este caso, el principio de varianza es superaditivo. De manera análoga, el principio de varianza es subaditivo si 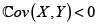 y aditivo si
y aditivo si 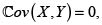 esto es, cuando los riesgos son no correlacionados. Debemos recordar en este punto que la independencia implica la no correlación, pero en general el recíproco no es cierto, pues puede darse el caso de riesgos no correlacionados dependientes; Mari & Kotz [6].
esto es, cuando los riesgos son no correlacionados. Debemos recordar en este punto que la independencia implica la no correlación, pero en general el recíproco no es cierto, pues puede darse el caso de riesgos no correlacionados dependientes; Mari & Kotz [6].
Prima del riesgo X + Y bajo el principio de desviación estándar. Para a > 0,
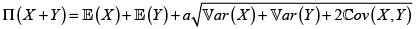
Para decidir sobre la (sub, super)-aditividad debemos comparar ahora este valor con 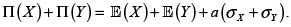 Dado que el coeficiente de correlación lineal de X y Y es menor o igual a 1, se concluye que el principio de desviación estándar es subaditivo.
Dado que el coeficiente de correlación lineal de X y Y es menor o igual a 1, se concluye que el principio de desviación estándar es subaditivo.
Prima del riesgo X + Y bajo el principio de varianza modificada. Para a > 0
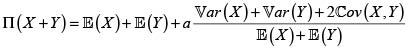
Para decidir sobre la (sub, super)-aditividad debemos comparar ahora este valor con
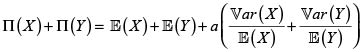
Para 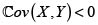 este principio de prima es subaditivo; Rolski et ál. [5].
este principio de prima es subaditivo; Rolski et ál. [5].
En el estudio de la prima de X + Y de la sección 4 usaremos estos tres principios de prima junto con algunas cópulas arquimedianas.
2. CÓPULAS
Durante las últimas décadas la teoría de cópulas se ha constituido en una herramienta esencial para el tratamiento de las estructuras de dependencia entre v. a. Este aspecto hace de esta teoría un elemento esencial para el desarrollo que nos hemos propuesto; por tanto, presentamos a continuación los conceptos y resultados de la teoría de cópulas que serán de interés a lo largo del artículo.
En esencia una cópula es una función que junta o acopla una fd multivariada a sus fd marginales unidimensionales Nelsen [7]. Dado el propósito de la teoría de cópulas en este artículo, centraremos este repaso en las cópulas bidimensionales.
Sean X y Y v.a. continuas con fd respectivas F(x) = P(X < x) y G(y) = P(Y < y) y fd conjunta H (x,y) = P(X < x, Y < y). Luego, para todo 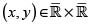 (
(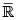 es llamado el conjunto de los reales extendidos [–∞, ∞]); consideremos los puntos sobre la 3– caja I3 = I × I × I ×, con I = [0,1], cuyas coordenadas están dadas por IF(x), G(y), H(x,y)), se tiene entonces que una proyección de este estilo, que va de I2 en I, es llamada una cópula bivariada. De manera un poco más formal, podemos definir una cópula bivariada como se indica a continuación.
es llamado el conjunto de los reales extendidos [–∞, ∞]); consideremos los puntos sobre la 3– caja I3 = I × I × I ×, con I = [0,1], cuyas coordenadas están dadas por IF(x), G(y), H(x,y)), se tiene entonces que una proyección de este estilo, que va de I2 en I, es llamada una cópula bivariada. De manera un poco más formal, podemos definir una cópula bivariada como se indica a continuación.
Definición 1 (Cópula). Una cópula bidimensional, (también llamada una 2-cópula) es una función C que satisface las siguientes propiedades:
• Dom(C) = I × I
• C(u,0) = C(o,v) = 0, esto es, es aterrizada (grounded).
• C(u,1) = u y C(1,v) = u
• ∀a1 < a2 y ∀b1 < b2, C(a1,b1) + C(a2,b2) – C(a1,b2) – C(a2,b1) > 0, es decir, es 2-creciente.
Por otra parte sabemos que F(x) y G(y) se encuentran en el intervalo [0,1]; por lo tanto, es pertinente establecer la relación u = F(x) y que v = G(y), que se encuentran en el dominio de la función C, de tal manera que la C(u,v) = C(F(x),G(y)) y de esta manera se logra establecer' una relación entre las marginales de las variables aleatorias X y Y y una función bivariada que estamos llamando cópula; una relación de este estilo es presentada por Sklar [8], quien en su teorema plasma la relación existente entre las funciones de distribución marginales, de dos o más variables y su respectiva función de distribución conjunta, a través de un modelo cópula, estableciendo con él la importante relación entre la teoría de cópulas y el modelado en estadística.
Teorema de Sklar
Sea H la función de distribución conjunta de dos variables aleatorias X y Y con marginales respectivas F y G. Entonces existe una cópula C tal que 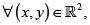 se cumple
se cumple
H(x,y) = C[F(x), G(y)].
Si F y G son continuas, entonces C es única; además la cópula C está únicamente determinada sobre Ran (F) × Ran(G), producto cartesiano de los rangos. De manera análoga, si C es una cópula y F y G son fd, entonces la fd conjunta H dada arriba como la cópula evaluada en las marginales, es una fd conjunta para las v. a. X y Y.
El teorema de Sklar es un resultado fundamental para el desarrollo de nuestro objetivo, puesto que demuestra que es posible separar la estructura de dependencia de las distribuciones marginales; de manera recíproca, también permite construir una distribución multivariada a partir del conjunto de distribuciones marginales y de la selección de una cópula. La estructura de dependencia es capturada en la función cópula y es independiente de las formas de las distribuciones marginales.
En la práctica es usual disponer de las distribuciones de pérdidas para los riesgos por separado. Por lo general, se tiene poco entendimiento de las posibles asociaciones o dependencias entre los distintos tipos de riesgos. Sin embargo, se reconoce el hecho de que puede haber vínculos. El teorema de Sklar nos permite experimentar con diferentes cópulas manteniendo idénticas distribuciones marginales.
Definición 2. Inversa generalizada o función cuantil
La inversa generalizada o función cuantil de la fd F se define por
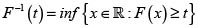
La cantidad xt = F–1(t) define el cuantil t de F.
Corolario 1. (Corolario del teorema de Sklar) Se definen H, , F y G como en los enunciados anteriores, y F–1 y G–1 como las respectivas funciones inversas generalizadas de F y G. Entonces ∀(u,v) ∈ [0,1]2,
c(U,v) = H(F–1(x), G–1(y)).
Definición 3. (Densidad de una cópula). Si existe, la densidad h de una fd H, se define como:
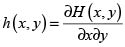
La expresión de la densidad de una cópula, simbolizada por c, es:
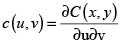
A partir de c(u,v), la densidad h de la función de distribución H puede obtenerse con h(x,y) = c(F(x),G(y)) f(x)g(y), donde f(x) y g(y) son las respectivas densidades de X y Y.
A continuación presentamos algunas propiedades de las cópulas:
1. Continuidad. Una cópula C(u,v) es continua en u y en v. Una cópula satisface la condición fuerte de Lipschitz:
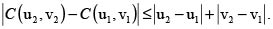
2. Diferenciabilidad. Dado que C(u,v) es 2– creciente y continua en ambas variables, es entonces diferenciable en casi todas partes, y
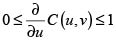 y
y 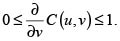
Si bien existen diferentes clases de cópulas, centraremos este estudio a la clase de las cópulas arquimedianas, dado que sus propiedades resultan de gran interés en aplicaciones al sector asegurador; y dentro de esta clase, pondremos nuestra atención en las familias de Frank y Ali-Mikhail-Haq.
Definición 4. (Cópula arquimediana). Sea φ una función continua, estrictamente decreciente de [0,1] sobre [0, ∞] tal que φ(1) = 0, y φ–1 es la función pseudo inversa de φ. Sea C la función definida de [0,1]2 sobre [0,1] tal que C(u,v) = φ–1[φ(u) + φ(v)]. Esta función es cópula si y solo si φ es convexa; y será llamada cópula arquimediana.
La función φ de la definición anterior es llamada generadora de la cópula.
2.1 Medida de dependencia tau de Kendall, τK
Se sabe que el coeficiente de correlación lineal es una función de las distribuciones marginales. Por ejemplo, cambiando la forma de las marginales cambiará necesariamente el valor del coeficiente de correlación. Al describir la dependencia utilizando cópulas, sería mucho más natural que las medidas de dependencia se determinaran solo por la cópula y no por las distribuciones marginales, porque la cópula no depende de la forma de los marginales y la dependencia es capturada de manera exclusiva por la cópula.
Por fortuna hay disponibles tales medidas de dependencia. Las dos medidas de asociación más conocidas son la ro de Spearman y la tau de Kendall, desarrolladas originalmente en el campo de la estadística no paramétrica. Recordaremos acá solo la medida de dependencia tau de Kendall, por ser más popular en el modelado con cópulas.
Sean (x,y) y (x',y') dos observaciones de un vector aleatorio (X,Y) entonces diremos que (x,y) y (x',y') son concordantes si(x – x')(y – y') > 0; en caso contrario diremos que son discordantes.
Definición 5. (Tau de Kendall, τK ). Sea (X,Y) un vector aleatorio. La medida de concordancia τK de Kendall se define como la diferencia entre las probabilidades de concordancia y discordancia de dos observaciones distintas,(x,y) y (x',y'), del vector aleatorio:
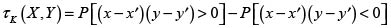
τK tiene las siguientes propiedades:
• –1 < τK < 1
• Si X e Y son concordantes, entonces, τK = 1.
• Si X e Y no son concordantes, entonces, τK = –1.
• Si X e Y son independientes entonces, τK = 0. La implicación inversa no necesariamente se cumple.
• Si α y β son dos funciones estrictamente crecientes, entonces τK[α(X), β(Y)] = τK(X,Y). Esto es, el coeficiente de correlación de Kendall permanece invariante ante una transformación estrictamente creciente de las v.a.
• τK no depende de la cópula de (X, Y).
Si la cópula es absolutamente continua, entonces elτK se puede expresar de la siguiente manera:
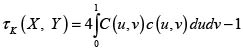
Para las cópulas arquimedianas se tiene
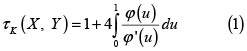
2.2 Dependencia en la cola
La ocurrencia de pérdidas extremas se encuentra entre las principales preocupaciones de quienes tienen la responsabilidad de gestionar el riesgo y su volatilidad potencial. Cuando hay dependencia entre v.a. de pérdidas, es necesario entender el comportamiento conjunto de tales variables cuando se producen resultados extremos. Se ha observado que si ocurren resultados extremos en uno de los riesgos, puede haber mayor probabilidad de resultados extremos en otros riesgos. Se ha sugerido que, si bien en tiempos normales la correlación puede ser pequeña, esta puede llegar a ser significativa en malos tiempos, como si todo pareciera ir mal a la vez. El concepto de dependencia en la cola aborda esta cuestión. Se han desarrollado varias medidas de dependencia en la cola para evaluar qué tan fuerte es la correlación en los grandes (pequeños) valores.
Definición 6. (Índice de dependencia en la cola superior, λU) Para las v.a X y Y con fd respectivas F y G, se define el índice de dependencia en la cola superior como
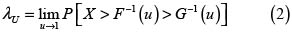
El índice de dependencia en la cola superior mide la posibilidad de que X tome un gran valor, si se sabe que Y toma un gran valor, donde el gran valor es medido en términos de percentiles equivalentes. Como λU es una probabilidad, entonces λU∈[0,1]. Si U y V son v.a. uniformes en (0,1), entonces podemos rescribir (2) como
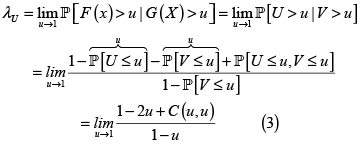
La fórmula (3) muestra que λU también puede expresarse en términos de la cópula en lugar de hacerlo con las distribuciones originales. Existe también el concepto de Índice de dependencia en la cola inferior, λL, pero dado que nuestro interés se centra en la cola derecha o superior, no lo presentamos. El índice de dependencia en la cola es una medida muy útil en la descripción de una cópula y sirve para comparar dos cópulas.
3. DEPENDENCIA POSITIVA Y DEPENDENCIA NEGATIVA
Sean X y Y dos riesgos con fd marginales respectivas F(x) y G(y) y fd conjunta H(x,y). Son conocidas las respectivas cotas inferior y superior de Fréchet para H ([6, 7, 9]):
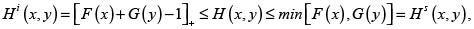
donde (a)+ = max(0,a).
A la familia de todas las distribuciones bivariadas con marginales conocidas F y G las denotamos por 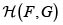 (o
(o 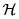 cuando no es necesario especificar las fd marginales), y escribimos, dependiendo del contexto,
cuando no es necesario especificar las fd marginales), y escribimos, dependiendo del contexto, 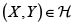 o
o 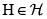 . Si X y Y son riesgos con dependencia positiva, escribimos
. Si X y Y son riesgos con dependencia positiva, escribimos 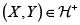 o
o 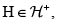 siempre que X y Y (F y G) verifiquen las condiciones de Kimeldorf & Sampson indicadas a continuación.
siempre que X y Y (F y G) verifiquen las condiciones de Kimeldorf & Sampson indicadas a continuación.
3.1 Condiciones de Kimeldorf & Sampson
La subfamilia 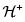 de riesgos con dependencia positiva verifica las siguientes propiedades ([10]):
de riesgos con dependencia positiva verifica las siguientes propiedades ([10]):
1. Para todo x y todo 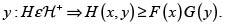 Esta condición se denomina dependencia PQD, y se estudia en la siguiente sección.
Esta condición se denomina dependencia PQD, y se estudia en la siguiente sección.
2. Si 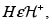 entonces
entonces 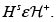
3. Si 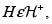 entonces
entonces 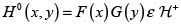
4. Si 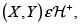 entonces, para toda función creciente φ,
entonces, para toda función creciente φ, 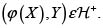
5. Si 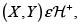 entonces
entonces 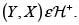
6. Si 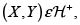 entonces
entonces 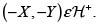
7. Si 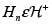 y
y 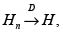 entonces
entonces 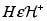 donde el símbolo D significa ''convergencia en distribución''.
donde el símbolo D significa ''convergencia en distribución''.
3.2 Dependencia cuadrante-positiva (-negativa), PQD (NQD)
Los riesgos X y Y con fd conjunta H y marginales respectivas F y G tienen dependencia cuadrante positiva, o son PQD, si y solo si
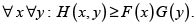 (4)
(4)
La ecuación (4) es equivalente a
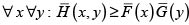 , (5)
, (5)
donde
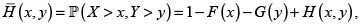
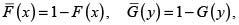
son las probabilidades de excedencia o funciones de supervivencia conjunta y marginales de H, F y G, respectivamente.
Si se invierte la desigualdad (4) o la (5), obtenemos la definición de dependencia cuadrante-negativa o NQD. Las distribuciones PQD satisfacen las condiciones de Kimeldorf & Sampson; [10]. A continuación presentamos un lema necesario para la prueba del resultado central ulterior. El lema se debe a Hoëffding, el cual en 1940 apareció en una publicación poco conocida, y fue reimpreso en la compilación de sus trabajos por Fisher & Sen [6, 11].
Lema. Hoëffding
Para los riesgos X y Y con marginales respectivas F(x) y G(y), fd conjunta H(x,y) y esperanza finita 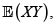 se verifica
se verifica
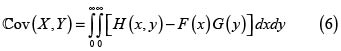
Nota. En realidad el lema se verifica en general para v. a. con soporte en los reales. Acá tratamos con riesgos, v. a. no negativas con esperanza finita.
Demostración: Para todo u,v > 0 se verifica 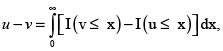 donde I denota la función indicadora. La justificación es por casos, de acuerdo con el orden de los números u y v. La presentamos para el caso u > v:
donde I denota la función indicadora. La justificación es por casos, de acuerdo con el orden de los números u y v. La presentamos para el caso u > v:
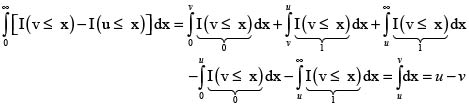
Por tanto,
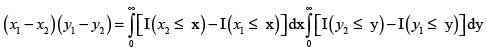
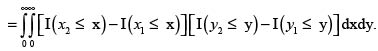
Ahora, sean (X1,Y1) y (X2,Y2) dos parejas independientes e idénticamente distribuidas con iguales distribuciones que (X,Y). Entonces se tiene
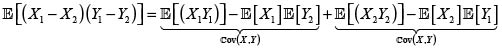
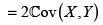
En consecuencia,
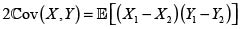
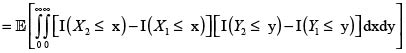
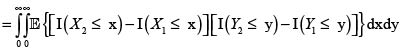
donde hemos podido intercambiar la esperanza con las integrales por la finitud de 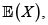
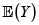 y
y 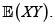 Por consiguiente,
Por consiguiente,
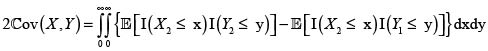
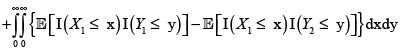
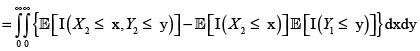
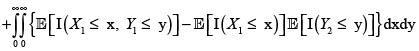
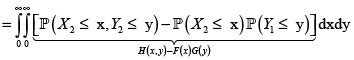
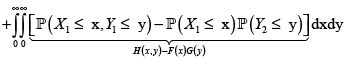
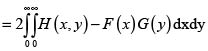
La siguiente proposición se basa en el lema anterior y es de importancia principal para el objetivo buscado. Su prueba es una consecuencia inmediata de la definición de variables PQD (NQD) y el lema de Hoëffding [6, 12].
Proposición 1
Para los riesgos X y Y con marginales respectivas F(x) y G(y), fd conjunta H(x,y) y esperanza finita 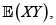 se verifica
se verifica
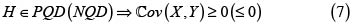
En la siguiente sección estudiaremos la prima de la suma de dos riesgos con dependencia PQD (NQD).
4. PRIMA DE LA SUMA DE DOS RIESGOS CON DEPENDENCIA DESCRITA POR CÓPULAS ARQUIMEDIANAS
Supongamos que X y Y son dos riesgos con marginales respectivas F y G. Estudiamos a continuación la prima del riesgo X + Y bajo el supuesto que la estructura de dependencia de los riesgos X y Y es capturada por algunas cópulas arquimedianas en modelado de riesgos dependientes, a saber, la de Frank y la Ali-Mikhail-Haq.
Sabemos por el Teorema de Sklar, que si C(u,,v) es la cópula que describe la estructura de dependencia de los riesgos X y Y, entonces la fd conjunta de X y Y es
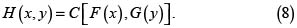
y su densidad conjunta es
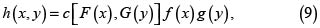
donde f y g son las densidades respectivas de X y Y y
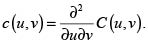
En este momento podemos calcular la varianza de la v.a. X + Y usando el Lema de Hoëffding:
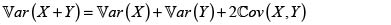
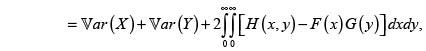
sabiendo que el signo del integrando determina si la distribución H es PQD o NQD, con lo cual quedan determinados los valores de las primas según los tres principios en estudio en el presente artículo.
Para estudiar la distribución del riesgo X + Y, usaremos el siguiente resultado presentado en no pocos textos de probabilidad, p. e. [13]:
Sean las v. a. X y Y con densidades marginales respectivas f y g y densidad conjunta h. Sea 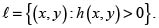 Supongamos que
Supongamos que
i. s = m(x,y) y q = n(x,y) definen una transformación uno a uno de 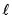 a
a 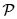 .
.
ii. Las primeras derivadas parciales de x = m–1(s,q) y y = n–1(s,q) son continuas sobre 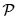 .
.
iii. El (determinante) jacobiano de la transformación es no nulo para 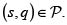
Entonces la densidad conjunta de las v.a. S = m(X,Y) y Q = n(X,Y) está dada por
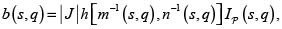 (10)
(10)
donde |J| es el valor absoluto del jacobiano
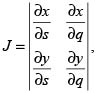
e 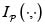 es la función indicadora.
es la función indicadora.
Con este resultado procedemos a calcular la densidad marginal de X + Y definiendo las v.a. S = m(X,Y)=X + Y y Q = n(X,Y) = X/Y, para Y = 0. El objetivo principal es hallar la densidad marginal de S, pero como resultado adicional podemos encontrar también la de Q. Para las funciones m y n indicadas la ecuación (10) toma la forma
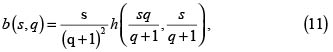
pues 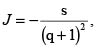 y s > 0. Así, la densidad marginal de S es
y s > 0. Así, la densidad marginal de S es
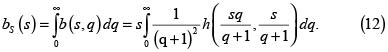
De manera análoga, la densidad marginal de Q es
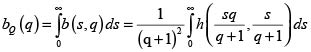
Con la densidad dada en (12) se calcula el valor esperado de S y su varianza, que también puede obtenerse a partir de (9). Con la densidad también obtenemos la fd de la v. a. 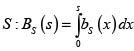 .?Esta fd se puede comparar con la fd de la v.a. X + Y bajo el supuesto de independencia entre X y Y, que como se sabe, está dada por
.?Esta fd se puede comparar con la fd de la v.a. X + Y bajo el supuesto de independencia entre X y Y, que como se sabe, está dada por
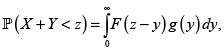 cuando las v. a. X y Y son independientes.
cuando las v. a. X y Y son independientes.
Es evidente que también es posible calcular el valor en riesgo de S a un nivel especificado α ∈ [0,1](VaRα(S) o πα cuando no es indispensable indicar la v.a. (S) y el valor en riesgo condicional o 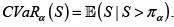 Recordamos que el VaRα(S) es el percentil α de la v.a. S. Es útil disponer de las siguientes expresiones para el C VaRα(S):
Recordamos que el VaRα(S) es el percentil α de la v.a. S. Es útil disponer de las siguientes expresiones para el C VaRα(S):
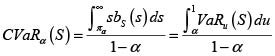
donde la segunda expresión se obtiene observando que VaRu (S) = s es equivalente a Bs (s) = u, por lo que Bs (s) ds = du.
Por otra parte, usando la variable exceso de pérdida de S
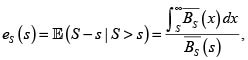
se obtiene sin dificultad otra expresión usual para el valor en riesgo condicional de S, a saber:
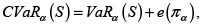
con lo cual se evidencia que el CVaR es mayor que el correspondiente VaR en una cantidad igual al promedio de las pérdidas que exceden el VaR.
En el resto de la sección veremos dos cópulas arquimedianas con un único parámetro θ usadas en modelos de riesgos dependientes. En cada una de ellas mostraremos un ejemplo numérico concreto para ilustrar los conceptos vistos y el rol del parámetro θ en la determinación de la positividad o negatividad de la dependencia de las v. a. X y Y estudiadas.
4.1 Cópula de Frank
La función generadora de la cópula de Frank es
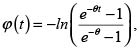
y la fd de la cópula es
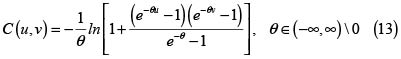
Esta cópula es PQD para valores de θ positivos y NQD para valores de θ negativos, y tiende a la cópula independencia cuando θ tiende a cero.
4.2 Cópula Ali-Mikhail-Haq
La función generadora de la cópula de Ali-Mikhail-Haq es
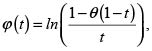
y la fd de la cópula es
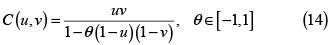
Esta cópula es PQD para valores de θ positivos y NQD para valores de θ negativos, y contiene a la cópula independencia cuando θ = 0.
4.3 Ejemplos numéricos
Presentamos a continuación algunos ejemplos para las cópulas arquimedianas uniparamétricas de Frank y Ali-Mikhail-Haq realizados con la ayuda del programa R [14] y la biblioteca cópula [15, 16]. Para esto fijaremos dos distribuciones marginales para las v. a. X y Y. Suponemos que X tiene distribución inversa de Gauss (o distribución de Wald) con parámetros v = 10 y λ = 15.62498 (X ∼ InvGauss(v,λ)) y Y tiene distribución lognormal con parámetros μ = 2 y σ = 0.85308111 (Y ∼ LNorm(μ,σ)). Así, 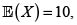
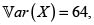
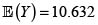 y
y 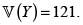 El valor esperado de X + Y es
El valor esperado de X + Y es 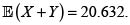 La varianza del riesgo X + Y bajo el supuesto de independencia, es
La varianza del riesgo X + Y bajo el supuesto de independencia, es 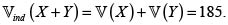
Ejemplo 1. (Cópula de Frank con θ = 2
Como vimos, la cópula de Frank con θ > 0 es PQD, la covarianza entre X y Y es positiva. Usando (8) obtenemos la fd H(X,Y), y con el Lema de Hoëffding (6) calculamos la covarianza: 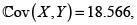 y por tanto,
y por tanto, 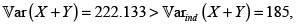 con lo cual podemos calcular las primas de la suma de los riesgos X y Y. La tabla 1 contiene los resultados. Los valores del coeficiente a para los principios de prima de desviación estándar y de varianza modificada fueron calculados para que la prima bajo el supuesto de independencia entre las variables aleatorias X y Y fueran iguales. No es difícil probar que al calcular de esta forma los valores de los coeficientes a, las primas con el principio de varianza y de varianza modificada son iguales. No obstante, cuando se suman las primas de X y de Y, los valores de estas son diferentes bajo los principios de primas mencionados.
con lo cual podemos calcular las primas de la suma de los riesgos X y Y. La tabla 1 contiene los resultados. Los valores del coeficiente a para los principios de prima de desviación estándar y de varianza modificada fueron calculados para que la prima bajo el supuesto de independencia entre las variables aleatorias X y Y fueran iguales. No es difícil probar que al calcular de esta forma los valores de los coeficientes a, las primas con el principio de varianza y de varianza modificada son iguales. No obstante, cuando se suman las primas de X y de Y, los valores de estas son diferentes bajo los principios de primas mencionados.
Se observa en todos los casos, que, como era de esperarse, al haber dependencia PQD entre los riesgos, la prima considerando la dependencia, ΠDep (X + Y), es mayor que si se supone la independencia entre los riesgos X y Y, ΠInd(X + Y). La tabla 2 muestra el VaR y el CVaR para diferentes valores de -. Como se sabe, el 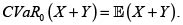
La figura 1 muestra la función de supervivencia (o de probabilidad de excedencia) de la v.a. en estudio X + Y bajo el supuesto de independencia y de dependencia. Se observa que las curvas se cortan.
Como en este caso la dependencia es PQD, entonces, en la cola de la distribución, la probabilidad de que la suma sea mayor que un valor especificado, es mayor en el caso de dependencia que en el de independencia. Caso contrario ocurriría si las v.a. fueran NQD (véase el siguiente ejemplo).
Por último, usando (1), τK = 0.214 y con (3), λU = 0. La biblioteca copula de R tiene los comandos adecuados para calcular ambas medidas.
Ejemplo 2. (Cópula de Frank con θ = –2)
Como vimos, la cópula de Frank con θ < 0 es NQD, la covarianza entre X yY es negativa: 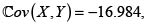 por tanto,
por tanto, 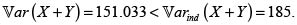 La tabla 3 contiene las primas de riesgo. Son válidos también acá, y en los siguientes ejemplos, los comentarios sobre los coeficientes a indicados arriba.
La tabla 3 contiene las primas de riesgo. Son válidos también acá, y en los siguientes ejemplos, los comentarios sobre los coeficientes a indicados arriba.
Se observa que al haber dependencia NQD entre los riesgos, la prima considerando la dependencia, ΠDep(X + Y) es menor que si se supone la independencia entre los riesgos X y Y, ΠInd(X + Y).
La figura 2 muestra la función de supervivencia de la v. a. X + Y bajo el supuesto de independencia y de dependencia. Las curvas se cortan. Como en este caso la dependencia es NQD, entonces, en la cola de la distribución, la probabilidad de que la suma sea mayor que un valor especificado, es mayor en el caso de independencia que en el de dependencia, como se había anticipado en el ejemplo anterior. La tabla 4 muestra el VaR y el CVaR para diferentes valores de α.
Por último τK = –0.214, el negativo de la cópula de Frank(2), y λK = 0.
Ejemplo 3. (Cópula Ali-Mikhail-Haq con θ = 0.9)
Como vimos, la cópula Ali-Mikhail-Haq con θ > 0 es PQD, la covarianza entre X y Y es positiva. Usando (8) obtenemos la fd H(X,Y), y con el Lema de Hoëffding (6) calculamos la covarianza 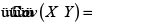 y por tanto,
y por tanto, 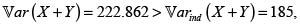 con lo cual podemos calcular las primas de la suma de los riesgos X y Y. La tabla 5 contiene los resultados. Son válidos también acá los comentarios sobre los coeficientes a en el primer ejemplo.
con lo cual podemos calcular las primas de la suma de los riesgos X y Y. La tabla 5 contiene los resultados. Son válidos también acá los comentarios sobre los coeficientes a en el primer ejemplo.
Se observa en todos los casos, que al haber dependencia PQD entre los riesgos, la prima considerando la dependencia, ΠInd(X + Y), es mayor que si se supone la independencia entre los riesgos X y Y ΠDep (X + Y). La tabla 6 muestra el VaR y el CVaR para diferentes valores de α.
Por último τ = 0.278 y λU = 2.98 × 10–8.
Ejemplo 4. (Cópula Ali-Mikhail-Haq con θ = –0.9
La cópula Ali-Mikhail-Haq con θ < 0 es NQD, la covarianza entre X y Y es negativa. Usando (8) obtenemos la fd H(X,Y), con el Lema de Hoëffding (6) calculamos la covarianza: 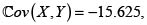 y por tanto,
y por tanto, 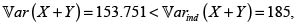 con lo cual podemos calcular las primas de la suma de los riesgos X y Y. La tabla 7 contiene los resultados. Son válidos también los comentarios sobre los coeficientes a en el primer ejemplo.
con lo cual podemos calcular las primas de la suma de los riesgos X y Y. La tabla 7 contiene los resultados. Son válidos también los comentarios sobre los coeficientes a en el primer ejemplo.
Al haber dependencia NQD entre los riesgos, ΠDep(X + Y) < ΠInd (X + Y). La tabla 8 muestra el VaR y el CVaR para diferentes valores de α.
Por último τK = –0.166 y λU = 0.
CONCLUSIONES
Las cópulas proveen una posibilidad de gran versatilidad para capturar la dependencia entre riesgos cuando se conocen las distribuciones de probabilidad marginales. Estudiar dos riesgos en conjunto con estas herramientas brinda la posibilidad de saber su comportamiento conjunto: ¿qué le pasa, en términos de probabilidad, a un riesgo si el otro toma un gran (pequeño) valor?, ¿cuál podría ser la prima de riesgo si se contrata una póliza para cubrir ambos riesgos?, ¿será menor o mayor que la suma de ambos tomados como si fueran independientes?
En el artículo solo se ha mostrado un par de cópulas arquimedianas con un solo parámetro, ambas con la posibilidad de mostrar dependencia PQD o NQD, pero es posible aplicar la metodología a otras cópulas arquimedianas uniparamétricas o de más parámetros. Es obvio que para hacerlo en la práctica se debe disponer de un número suficiente de datos y se deben usar técnicas de ajustes de cópulas, aspecto que está por fuera del alcance del presente artículo, pero para el cual existe ya extensa bibliografía. Véase por ejemplo [9], y la bibliografía citada en él, en particular el algoritmo de Klugman & Parsa, p. 489.
Es de gran utilidad disponer de la posibilidad de calcular el valor en riesgo y el valor en riesgo condicional del riesgo X + Y para un nivel de seguridad dado cuando se considera la dependencia entre los riesgos. De esta forma se afina la medida del riesgo visto en conjunto y se evita caer en una sobrevaloración o subvaloración de la prima de riesgo.
Notas:
* Artículo resultado de investigación derivado del proyecto: órdenes estocásticos, medidas de riesgo y programación estocástica, cofinanciado por la Universidad de Medellín y la Universidad EAFIT.
REFERENCIAS
[1] Hutchinson, T. and Lai, C. (1990). Continuous Bivariate Distributions, Emphasing Applications. Adelaide: Rumsby.
[2] Kotz, S., Balakrishnan, N. and Johnson, N. (2000). Continuous Multivariate Distributions. Vol. 1, Models and Applications, New York: Wiley.
[3] Mardia, K. (1970). Families of Distributions Bivariates. London. Griffin.
[4] Teugels, J. L.; Sundt, B. Encyclopedia of Actuarial Science. Wiley, 2004.
[5] Rolski, T.; Schmidli, H.; Schmidt, V.; Teugels, J. Stochastic Processes for Insurance and Finance. Wiley, 1999.
[6] Mari, D. D. and Kotz, S. (2001). Correlation and Dependence. Imperial College Press.
[7] Nelsen, R. (2006). An Introduction to Copulas. Second Edition. New York: Springer.
[8] Sklar, A. (1959). Fonctions de répartition a n dimensions et leurs marges. Publications de l'Institut de Statistique de l'Université de Paris, 8, 229-231.
[9] Klugman, Stuart A.; Panjer, Harry H.; Willmot, Gordon E. (2008). Loss Models. From Data to Decisions. Third Edition. Wiley.
[10] Kimeldorf, G.; Sampson, A. R. Positive dependence orderings. Annals of the Institute of Statistical Mathematics, 39, Part A, 113-128, 1987.
[11] Hoëffding, W. Collected Works. Editors: N. I. Fisher \& P. K. Sen, Springer, (1994).
[12] Lehmann, E. L. Some concepts of dependence. Annals of Mathematical Statistics, 37, 1137-1153, 1966.
[13] Mood, A; Graybill, F; Boes, D. Introduction to the Theory of Statistics. McGrawHill. Third Edition, 1974.
[14] R Development Core Team (2011). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0, URL http://www.R-project.org/.
[15] Yan, Jun (2007). Enjoy the Joy of Copulas: With a Package copula. Journal of Statistical Software, 21(4), 1-21. URL http://www.jstatsoft.org/v21/i04/.
[16] Kojadinovic, Ivan; Yan, Jun (2010). Modeling Multivariate Distributions with Continuous Margins Using the copula R Package. Journal of Statistical Software, 34(9), 1-20. URL http://www.jstatsoft.org/v34/i09/.