ARTÍCULOS

Balance horizontal de líneas de ensamble para modelos mixtos

Horizontal balancing for mixed models assembly lines

Luis Felipe Durango Cruz^*; Juan Pablo Orejuela Cabrera^**; Luis Alberto Ortiz Dorado^***

* Ing., Escuela de Ingeniería Industrial y Estadística, Universidad del Valle, calle 13 N.° 100–00, +57 (2) 333–4903 fdurango@univalle.edu.co

** MSc, Escuela de Ingeniería Industrial y Estadística, Universidad del Valle, calle 13 N.° 100–00, +57 (2) 333–4903, juan.orejuela@correounivalle.edu.co;

*** Ing., Escuela de Ingeniería Industrial y Estadística, Universidad del Valle, calle 13 N.° 100–00, +57 (2) 333–4903 luisorti@correounivalle.edu.co

Recibido: 15/10/2013
Aceptado: 12/12/2014

Resumen

Las líneas de ensamble tradicionalmente han sido utilizadas para producir grandes cantidades de un único modelo. Para aprovechar las ventajas de estas en ambientes de manufactura flexibles, se pueden implementar líneas de modelos mixtos las cuales permiten ensamblar diferentes productos de una familia en una misma línea; sin embargo, su balanceo requiere técnicas diferentes de las tradicionales. En esta investigación se hizo una revisión bibliográfica para analizar los factores que afectan las líneas de modelos mixtos y con base en esto se desarrolló un modelo de optimización matemática que estabiliza las cargas de trabajo, facilitando la decisión sobre las secuencias de producción que se programan en la línea. El modelo se corrió en varios escenarios y se obtuvieron resultados significativamente mejores que los obtenidos con un método tradicional de balance.

Palabras clave: balance de línea, modelos mixtos, balance horizontal.

Abstract

Traditionally assembly lines have been used to produce high volumes of a single model. To take advantage of these lines in flexible manufacturing environments, we can implement mixed model lines which allow manufacturing different products of a family in the same line, however, its balancing requires different techniques that traditional. In this research, a literature review was made to analyze the factors affecting the mixed model lines in MTO environments and based on this we developed a mathematical optimization model to stabilize workloads making easier the decision about production sequences that are programmed on the line. The model was run in several instances and the results were significantly better than those obtained with a line balancing traditional method.

Keywords: line balancing, mixed models, horizontal balancing.

INTRODUCCIÓN

Las líneas de ensamble originalmente fueron diseñadas para producir grandes cantidades de un único modelo. De acuerdo con [1] , estas son ideales para las fábricas que compiten en mercados tradicionales de consumo masivo y deben elaborar altos volúmenes de bienes estandarizados, ya que permiten alcanzar altos indicadores de productividad aprovechando al máximo la utilización de los recursos. Sin embargo, los mercados actuales son globalizados y despiertan en los clientes diferentes tipos de gustos que se renuevan constantemente. Para responder a estos patrones de demanda modernos es indispensable que las empresas ofrezcan un amplio portafolio de productos que puedan ser elaborados en bajas cantidades y en cortos tiempos de suministro; por lo tanto, es necesario que sus sistemas productivos sean lo suficientemente flexibles como para producir una combinación de productos que fuese requerida por los clientes, pero al mismo tiempo deben tener alta eficiencia. En estos casos se pueden utilizar líneas de ensamble para aprovechar sus ventajas, pero es necesario considerar nuevas técnicas de balance que permitan tener un mayor grado de flexibilidad. En este sentido la implementación de líneas de ensamble de modelos mixtos se presenta como una buena alternativa para afrontar esta problemática.

El concepto de modelos mixtos hace referencia a una familia que se compone por un conjunto de productos que se diferencian entre sí solamente por características menores, pero cuyas funciones principales son básicamente las mismas. Generalmente estos productos se ensamblan después de que el cliente defina sus requerimientos personales, y a pesar de que son diferentes, se desea que el proceso productivo sea similar para todos ellos; por lo tanto, es razonable pensar que cualquier combinación de estos se puede ensamblar en una misma línea, siempre y cuando los tiempos de alistamiento al pasar de un modelo a otro sean despreciables. Específicamente esta implementación se hace mucho más interesante dentro de ambientes de manufactura contra pedido o Make To Order, en los que llegan órdenes de trabajo de manera aleatoria, donde cada una de ellas tiene diferentes especificaciones. Por tanto, a diferencia del balance tradicional de línea, se requiere considerar otros factores tales como la mezcla o mix de demanda y la variación en los tiempos de operación para cada orden de trabajo.

De acuerdo con [2] , cuando en una línea de ensamble los productos no son completamente homogéneos, el tiempo de proceso de una misma tarea puede variar para cada uno de estos; por lo tanto, el tiempo de ciclo en las estaciones dependerá en gran medida del modelo específico que esté siendo ensamblado en cada momento. Si una línea de estas ha sido balanceada con técnicas tradicionales se pueden evidenciar ciertos problemas, pues probablemente esta no se encuentre en capacidad de producir de manera eficiente cualquier secuencia de órdenes de trabajo; estos problemas surgen cuando una estación trabaja en varios modelos que requieren un alto tiempo de proceso, seguido uno de otro, lo que hace que el tiempo de ciclo pueda ser excedido, produciendo una sobrecarga de trabajo que debe ser compensada por alguna medida correctiva que generalmente genera costos adicionales o deterioros en la calidad del producto. Según [2] , el problema del balance es interdependiente con el problema de la programación de operaciones, conocido como scheduling; por lo tanto, las sobrecargas podrían evitarse si se encuentra una secuencia de trabajo en la cual los modelos que requieren altos tiempos en una estación se alternan con los que requieren menos tiempo; sin embargo, si se balancean las cargas de trabajo dentro de cada estación para todos los modelos, el scheduling será un problema de menor importancia porque así cualquier secuencia podría tener una eficiencia aceptable en todas las estaciones.

1. REVISIÓN BIBLIOGRÁFICA

La implementación de líneas de ensamble de modelos mixtos es una estrategia utilizada en las últimas décadas para afrontar la creciente variedad de productos que se demanda por parte de los clientes. Según [3] , bajo estos enfoques de producción, las líneas tradicionales de grandes longitudes se remplazan por líneas que constan de pocas estaciones de trabajo donde no suele haber banda transportadora, lo que simplifica el sistema en cuanto al número de operaciones y bajos niveles de producto en proceso. Además de esto, la duración de una misma tarea puede variar dependiendo del tipo de modelo.

En el balance de líneas de modelos mixtos, la asignación de tareas comunes en diferentes modelos a las estaciones de trabajo es un aspecto que ha sido discutido por varios autores. En [4] , se sostiene que una tarea de estas debe desarrollarse en una única estación para todos los modelos; de esta manera habría mayor especialización de los operarios, y se ahorrarían costos al eliminar la necesidad de duplicar máquinas y equipos. Por otra parte en [3] , aseguran que podría existir una desventaja al asignar estas tareas a una misma estación, ya que se genera una fuerte interdependencia entre los modelos, lo que resulta en soluciones de menor calidad para el problema de balance de línea. Por este motivo, proponen un modelo matemático donde las tareas se dividen en dos conjuntos, uno en el cual las tareas se tienen que asignar a una misma estación y otro en el que se pueden asignar a diferentes estaciones. Estos planteamientos, y otros que se presentaran más adelante, fueron incorporados de manera integrada al modelo desarrollado en la presente investigación, ya que permiten optimizar la eficiencia en términos de tiempos ociosos y al mismo tiempo ayudan a evitar la duplicidad de máquinas de alto costo.

Otro aspecto que ha sido considerado en algunas investigaciones en líneas de modelos mixtos es la inclusión de líneas de dos lados como en [5, 6] ; otras investigaciones involucran la variabilidad en algunos de sus parámetros lo cual se puede ver en [7] y [8] ; por su parte en [9 – 11] emplean los enfoques multi–objetivo en las líneas de modelos mixtos; además, [12 – 14] introduce el problema de tiempos de alistamiento a este tipo de líneas.

De acuerdo con Scholl y Becker [15] existen dos enfoques para modelar y resolver los problemas de modelos mixtos; estos son la reducción a un único modelo y el balance horizontal.

1.1 Reducción a problema de único modelo

Este método consiste en simplificar el problema de modelos mixtos y abordarlo como si se tratara de una línea de modelo único; para esto se hace una transformación sencilla de los datos, que consiste en calcular el tiempo promedio w_k de cada tarea k. De acuerdo con Matanachai y Yano [16] una forma para calcular este promedio es la ecuación (1), donde m_j es la participación del modelo j en el mix de demanda y d_jk es la duración de la tarea k para el modelo j.

Al utilizar los tiempos promedio de cada tarea, el problema de modelos mixtos queda transformado en un problema de balance de líneas de ensamble simple, SALBP, por sus siglas en inglés. Resolviendo el problema resultante se garantiza que el tiempo de ciclo es suficiente para realizar todas las tareas en promedio; sin embargo, aun encontrando la solución óptima, podría haber tiempos ociosos y sobrecargas de trabajo considerables cuando se opere la línea, debido a las variaciones en los tiempos de operación de cada modelo en las estaciones.

1.2 Balance horizontal

El balance horizontal busca minimizar la variación entre las estaciones que representa la desviación de la carga de trabajo de cada modelo a través de las estaciones, mejorando así su tiempo de ciclo. Este enfoque ha sido abordado por varios autores desde la optimización implementando diferentes formas para la función objetivo.

Thomopoulos [17] propone la función objetivo (2), la cual minimiza la suma de las diferencias absolutas entre el tiempo promedio por estación 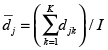del modelo j y su tiempo p_ij en cada estación i; siendo I el número total de estaciones.

Decker [18] propone la función objetivo (3), la cual minimiza la máxima diferencia absoluta entre el tiempo de estación p_ij y el tiempo promedio por estación 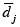de cada modelo.

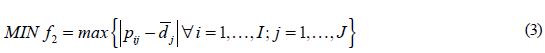
La función objetivo (4) propuesta por Domschke, et al. [19] minimiza la suma del tiempo resultante de las violaciones al tiempo de ciclo c de todos los modelos en todas las estaciones.

Matanachai y Yano [16] enriquecen el aporte de Thomopoulos [17] y proponen una función objetivo donde consideran tres componentes: uno para el balance tradicional, otro para la variación entre las estaciones e incorporan un nuevo concepto llamado variación dentro de las estaciones expresado en la ecuación (5) donde ρ representa la utilización promedio de la línea, que ayuda a reducir la desviación absoluta de los tiempos de proceso de los diferentes modelos dentro de cada estación. Si esta variación es pequeña, cualquier secuencia de producción tendrá bajas sobrecargas y la línea de ensamble estará preparada para cualquier cambio en el mix de demanda. Sin embargo, esto podría hacer que la carga de trabajo global esté balanceada en menor medida y se aumente levemente el tiempo de ciclo, pero con el beneficio de reducir la sobrecarga de trabajo.

La propuesta de trabajo desarrollada en esta investigación considera el enfoque de balance horizontal, de tal modo que su función objetivo se basa en el concepto de la variación entre estaciones presentado por Thomopoulos [17] , y en la variación dentro de las estaciones propuesta por Matanachai y Yano [16] ; sin embargo, a diferencia de estos autores, y como principal aporte de la investigación, este modelo permite la asignación de algunas tareas comunes a diferentes estaciones, lo que ayuda a tener soluciones de mejor calidad como lo sugieren Bukchin et al. [3] . El objetivo principal es balancear las cargas de trabajo de cada uno de los productos que pasan por la línea para facilitar el problema de la secuenciación.

2. METODOLOGÍA

2.1 Formulación matemática

Para modelar matemáticamente el problema, se definió la siguiente notación:

I, J, K número de estaciones, de modelos y de tareas; respectivamente

m_j participación del modelo j en el mix de demanda

d_jk duración de la tarea k para el modelo j

w_k carga de trabajo en promedio ponderado de la tarea k;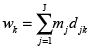

T carga de trabajo promedio total;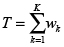

ρ utilización promedio de la línea;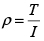

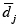duración promedio por estación del modelo j;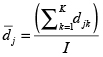

pij duración del modelo j en la estación i

IP_k conjunto de las predecesoras inmediatas de la tarea k

E conjunto de tareas en el cual cada tarea tiene que ser asignada a una misma estación para todos los modelos

La función objetivo (6) consta de dos componentes: el primero representa la variación entre las estaciones que ayuda a minimizar el tiempo de ciclo de cada modelo de manera independiente; el segundo representa la variación dentro de las estaciones, que ayuda a reducir la variabilidad de los tiempos de proceso dentro de cada estación para facilitar el scheduling. La variable de decisión X_ijk es una binaria que decide si la tarea k del modelo j se asigna a la estación i. Ambos componentes de la función objetivo son ponderados por la participación m_j de cada modelo j para darle mayor importancia a los modelos que tienen mayor demanda. El conjunto de restricciones (7) asegura que cada tarea de cada modelo sea asignada en una estación. El conjunto de restricciones (8) obliga a que se cumplan las relaciones de precedencia entre las tareas. Y el conjunto de restricciones (9) asegura que toda tarea que pertenezca al conjunto E sea asignada a una misma estación para todos los modelos que la requieren.

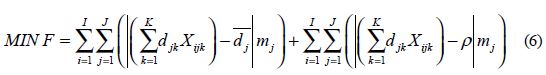
Sujeto a:

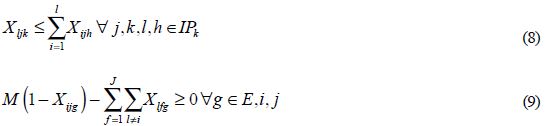
Antes de programar el modelo en el software de optimización, es necesario hacer una serie de modificaciones para que el modelo sea lineal sustituyendo el valor absoluto de la función objetivo (6). Para hacer esto se definieron las siguientes variables de decisión:

OUB_ijsobreutilización ocasionada por el modelo j en la estación i, para el balance entre las estaciones.

UUB_ijsubutilización ocasionada por el modelo j en la estación i, para el balance entre las estaciones.

C_ij 1, si la carga de trabajo del modelo j genera sobreutilización en la estación i, para el balance entre las estaciones; 0, de lo contrario.

OUW_ij sobreutilización ocasionada por el modelo j en la estación i, para el balance dentro de las estaciones.

UUW_ij subutilización ocasionada por el modelo j en la estación i, para el balance dentro de las estaciones.

D_ij 1, si la carga de trabajo del modelo j genera sobreutilización en la estación i, para el balance dentro de las estaciones; 0, de lo contrario.

La expresión (10) indica que cuando el modelo j tiene un tiempo 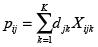en la estación i mayor que su tiempo promedio por estación 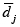, se genera una sobrecarga de trabajo en dicha estación con respecto a la variación entre las estaciones, lo cual se denomina sobreutilización OUB_ij, y en el caso contrario sería una subutilización UUB_ij. Análogamente la expresión (11) indica la sobreutilización OUW_ij o la subutilización UUW_ij ocasionada por el modelo j en la estación i que se generaría cuando hay una diferencia entre el tiempo p_ij y la utilización promedio de la línea ρ para la variación dentro de las estaciones. Haciendo la sustitución de las ecuaciones (10) y (11) en la función objetivo (6) se puede eliminar la función valor absoluto y controlar su efecto por medio de las restricciones (13) a (18), obteniendo la función objetivo (12), que es una función lineal equivalente.

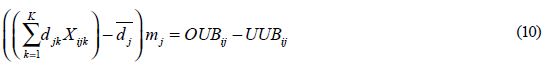
Donde si OUB > 0 entonces UUB_ij = 0; y si UUB_ij > 0 entonces OUB_ij = 0

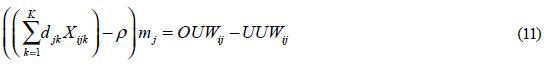
Donde si OUW_ij > 0 entonces, UUW_ij= 0; y si UUW_ij > 0 entonces OUW_ij= 0

Al hacer las sustituciones anteriores el modelo de programación lineal queda así:

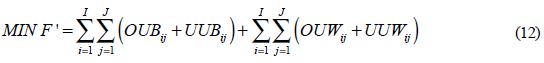
Sujeto a:

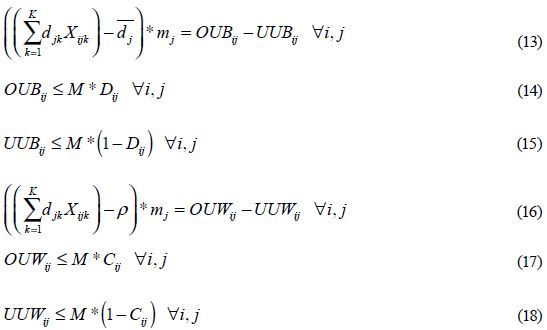
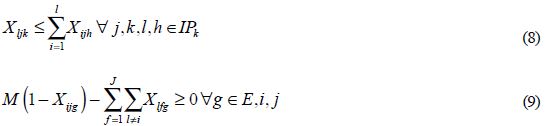
Los conjuntos de restricciones (14) y (15), aunque redundantes, aseguran que ante un valor positivo de la sobreutilización para el balance entre las estaciones, el valor de la subutilización sea igual a cero, y viceversa. Igualmente los conjuntos de restricciones (17) y (18) tienen el mismo efecto que los dos anteriores pero lo hacen para el balance dentro de las estaciones.

2.2 Caso de estudio

Para implementar el modelo y analizar sus efectos se consideró un caso de estudio con los siguientes parámetros:

I = 5 estaciones

J = 3 modelos

K = 15 tareas

m₁ = 25%, m₂ = 45%, m₃ = 30%.

ρ = 12.27

Los tiempos de tarea se presentan en la Tabla 1, y en la Figura 1 se muestran las relaciones de precedencia, donde las tareas que se encuentran dentro de cuadrados son las tareas que deben ser asignadas a una misma estación para todos los modelos.

3. COMPARACIÓN Y ANÁLISIS DE RESULTADOS

Computacionalmente el modelo propuesto fue programado en el software de optimización Lingo; en este caso consta de 361 variables de decisión y 497 restricciones; se corrió con el método de solución Branch and Bound y en un tiempo de 2 minutos usando 3 GB de memoria RAM se obtuvo la solución óptima.

Con la configuración obtenida los tiempos de tarea promedio w_k no se encuentran muy bien balanceados; sin embargo, esto no tiene mucha importancia, pues lo que se busca es estabilizar las cargas de trabajo de cada modelo. En la Figura 2 se puede observar la duración p_ij del modelo j en la estación i; aquí la variación entre las estaciones de acuerdo con la ecuación (2) es igual a 10 unidades de tiempo con lo que se logra que las cargas de trabajo de cada modelo sean altamente estables a través de la línea, la variación dentro de las estaciones de acuerdo con la ecuación (5) es igual a 21.73 unidades de tiempo, es decir, que dentro de cada estación hay una baja variabilidad en la carga de los modelos con lo que se consigue el objetivo de facilitar el problema del scheduling (ver Tabla 2).

3.1 Comparación de resultados

Para comparar los resultados obtenidos se planteó otra configuración para la línea basada en el enfoque de reducción a único modelo con una técnica de balance tradicional usando la función objetivo (19), la cual es una versión lineal de la propuesta por Matanachai y Yano [16] ; este modelo se basa en los tiempos de tarea promedio w_k, y minimiza las diferencias entre la utilización promedio de la línea ρ y el tiempo promedio por estación 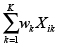, siendo X_ik una variable de decisión binaria que define si la tarea k se asigna a la estación i.

El conjunto de restricciones (20) a (22) garantiza que la sobreutilización OU_i o la subutilización UU_i en cada estación i tome el valor correspondiente según el caso, donde B_i es una variable de decisión binaria que es igual a 1 si en la estación i se produce una sobrecarga, y es igual a 0, en caso contrario. El conjunto de restricciones (23) garantiza cada tarea se asigne a una sola estación y el conjunto de restricciones (24) asegura que se cumplan las relaciones de precedencia.

Sujeto a:

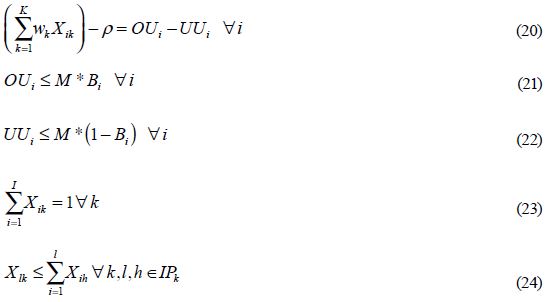
Los resultados obtenidos con este método se pueden observar en la Figura 3. Aquí el valor de la función objetivo (19) es igual a 0.72 unidades de tiempo, por lo que se puede decir que las cargas de trabajo promedio w_k se encuentran casi perfectamente balanceadas; sin embargo, aun así la variación entre las estaciones es igual a 24.4 unidades de tiempo y la variación dentro de las estaciones es igual a 33.19 unidades de tiempo (véase Tabla 2). En este caso el modelo 1 genera una carga de trabajo muy alta en la estación 5, por lo cual probablemente cada vez que este modelo pase por ahí, esta se encontrará bloqueada durante algún tiempo generando esperas para los modelos que vienen de la estación anterior. Igualmente en la misma estación el modelo 3 tiene una carga de trabajo muy baja lo que es causal de tiempos ociosos. Esto ocurre porque las tareas 7, 13, 14 y 15 fueron asignadas a la estación 5, pero la duración de estas es muy diferente para cada modelo. Por situaciones como estas se puede afirmar que el promedio no es adecuado para balancear la carga de todos los modelos. Con este tipo de balances se aumenta la dificultad para solucionar el problema de la secuenciación, ya que no se puede evitar el tener que programar los modelos que causan bloqueos o tiempos ociosos en las estaciones.

Para validar estos resultados se simuló en el software Promodel, la elaboración de un lote de 60 unidades en total con las dos configuraciones de la línea usando secuencias aleatorias, y en el 100 % de los casos el tiempo requerido para terminar el lote fue inferior hasta en un 10 % con la configuración del método propuesto. Esto sucede porque al minimizar la variación entre las estaciones se obtiene un tiempo de ciclo menor para cada modelo, y al minimizar la variación dentro de las estaciones se tiene la línea preparada para que haya un buen flujo en esta cuando cualquier secuencia de modelos pase por ella.

3.2 Análisis de sensibilidad

Finalmente, para validar la efectividad del modelo propuesto se hizo un análisis de sensibilidad donde se crearon varios escenarios con diferentes valores en los parámetros de participación en el mix m_j, número de modelos J, y número de estaciones I, y se compararon los resultados al balancear la línea con el método propuesto de balance horizontal y con el método de reducción a único modelo, obteniendo siempre una mejor estabilidad en las cargas de trabajo con el método propuesto. En los escenarios donde se varió el número de modelos J siempre se obtuvieron mejores resultados, excepto cuando se consideró J = 1, pues ahí la línea opera como si fuera de un único modelo y se obtiene la misma variabilidad de las cargas de trabajo con los dos métodos. Igualmente en los escenarios donde se varió la participación m_j los resultados obtenidos con el método propuesto siempre arrojaron cargas de trabajo más estables para todos los modelos, excepto en los escenarios donde se le asignó el 100 % de la participación a alguno de los tres modelos, ya que en estos casos la línea también estaría operando como una línea de modelo único. Y en los escenarios donde se varió el número de estaciones I se pudo observar que existe una tendencia creciente en la variación de las cargas de trabajo al aumentar el número de estaciones; sin embargo, los resultados siempre fueron más satisfactorios con el modelo propuesto.

4. CONCLUSIONES

El balance de las línea de modelos mixtos es un proceso complejo debido a la interdependencia que tiene con el problema de scheduling; esto se dificulta aún más en ambientes donde hay aleatoriedad en el orden de llegada de los pedidos lo cual hace que generalmente no se tengan muchas opciones para decidir sobre las secuencias de producción, y estas quedan estas al azar. El modelo propuesto contribuye a solucionar este problema, configurando la línea para que cualquier secuencia de producción tenga un desempeño aceptable en cuanto a tiempos ociosos, sobrecargas y tiempo requerido para elaborar un lote completo de modelos.

Al balancear cualquier línea de ensamble de modelos mixtos con el método propuesto se puede garantizar que las cargas de trabajo siempre sean estables para todos los modelos y todas las estaciones. Además, en todos los casos se puede afirmar que el enfoque de balance horizontal arroja mejores configuraciones de línea que el enfoque de reducción a único modelo.

El problema de las líneas de modelos mixtos es un tema que aún tiene muchos aspectos por investigar, especialmente la decisión conjunta entre el balance de línea y el scheduling para optimizar todo el proceso desde un enfoque sistémico.

REFERENCIAS

[1] J. Womack, D. Jones y D. Roos, ''La industria de las industrias se encuentra en transición'' en La máquina que cambió el mundo, 1–4 pp. México D. F.: McGraw Hill, 1992.

[2] N. Boysen, M. Fliedner y S. Armin, ''Assembly line balancing: Which model to use when?'', Int. J. Production Economics, vol. 111, n.° 2, pp. 509–528, 2008.

[3] J. Bukchin, E. M. Dar–El y J. Rubinovitz, ''Mixed model assembly line design in a make–to–order environment'', Computers & Industrial Engineer, vol. 41, n.° 4, pp. 405–421, 2002.

[4] A. Scholl, Balancing and secuencing of assembly lines, Heidelberg, Germany: Physica–Verlag, 1995.

[5] I. Kucukkoc and D. Z. Zhang, ''Mathematical model and agent based solution approach for the simultaneous balancing and sequencing of mixed–model parallel two–sided assembly lines'', Int. J. Prod. Econ., vol. 158, pp. 314– 333, Dec. 2014.

[6] B. Yuan, C. Zhang, X. Shao, and Z. Jiang, ''An effective hybrid honey bee mating optimization algorithm for balancing mixed–model two–sided assembly lines'', Comput. Oper. Res., vol. 53, pp. 32– 41, 2015.

[7] N. Manavizadeh, M. Rabbani, D. Moshtaghi, and F. Jolai, ''Mixed–model assembly line balancing in the make–to–order and stochastic environment using multi–objective evolutionary algorithms'', Expert Syst. Appl., vol. 39, n.° 15, pp. 12026–12031, 2012.

[8] L. Tiacci, ''Simultaneous balancing and buffer allocation decisions for the design of mixed–model assembly lines with parallel workstations and stochastic task times'', Int. J. Prod. Econ., 2015.

[9] B. Yagmahan, ''Mixed–model assembly line balancing using a multi–objective ant colony optimization approach'', Expert Syst. Appl., vol. 38, n.° 10, pp. 12453–12461, 2011.

[10] C. Yang, J. Gao, and L. Sun, ''A multi–objective genetic algorithm for mixed–model assembly line rebalancing'', Comput. Ind. Eng., vol. 65, n.° 1, pp. 109– 116, 2013.

[11] J. Oesterle and L. Amodeo, ''Efficient Multi–objective Optimization Method for the Mixed–model–line Assembly Line Design Problem'', Procedia CIRP, vol. 17, pp. 82– 87, 2014.

[12] S. Akpinar, G. Mirac Bayhan, and A. Baykasoglu, ''Hybridizing ant colony optimization via genetic algorithm for mixed–model assembly line balancing problem with sequence dependent setup times between tasks'', Appl. Soft Comput., vol. 13, n.° 1, pp. 574–589, 2013.

[13] S. Akpinar and A. Baykasoğlu, ''Modeling and solving mixed–model assembly line balancing problem with setups. Part I: A mixed integer linear programming model'', J. Manuf. Syst., vol. 33, n.° 1, pp. 177–187, 2014.

[14] S. Akpinar and A. Baykasoğlu, ''Modeling and solving mixed–model assembly line balancing problem with setups. Part II: A multiple colony hybrid bees algorithm'', J. Manuf. Syst., vol. 33, n.° 4, pp. 445–461, 2014.

[15] A. Scholl y C. Becker, ''State–of–the–art exact and heuristic solution procedures for simple assembly line balancing'', European Journal of Operations Research, vol. 168, n.° 3, p. 666–693, 2006.

[16] S. Matanachai y C. Yano, ''Balancing mixed–model assembly lines to reduce work overload'', IIE Transactions, vol. 33, n.° 1, p. 29–42, 2001.

[17] N. T. Thomopoulos, ''Mixed model line balancing with smoothed station assignments'', Management Science, vol. 16, n.° 9, pp. 593–603, 1970.

[18] M. Decker, ''Capacity smoothing and sequencing for mixed–model lines'', International Journal of Production Economics, vols. 30–31, pp. 31–42, 1993.

[19] W. Domschke, R. Klein y A. Scholl, ''Antizipative Leistungsabstimmung bei moderner Variantenfließfertigung'', Zeitschrift für Betriebswirtschaft, n.° 66, pp. 1465–1490, 1996.