ARTÍCULOS

Control del sobreajuste en redes neuronales tipo cascada correlación aplicado a la predicción de precios de contratos de electricidad

Overfitting control inside cascade correlation neural networks applied to electricity contract price prediction

Fernán A. Villa G.^*; uan D. Velásquez H.^**; Paola A. Sánchez S.^***

* Universidad Nacional de Colombia. Email: favilla0@unal.edu.co

** Universidad Nacional de Colombia. Email: jdvelasq@unal.edu.co

*** Universidad Simón Bolívar. Email: psanchez@unisimonbolivar.edu.co

Recibido: 11/12/2013
Aceptado: 12/12/2014

Resumen

La predicción de precios de electricidad es considerada una tarea difícil debido a la cantidad y complejidad de los factores que influyen en su representación, y sus relaciones. Las redes neuronales tipo cascada correlación – CASCOR– permiten, realizar un aprendizaje constructivo, capturando mejor las características de los datos; sin embargo, presentan una alta tendencia al sobreajuste. Para el control del sobreajuste en algunos ámbitos se usan técnicas de regularización. No obstante, en la literatura no existen estudios que: i) Utilicen técnicas de regularización para el control de sobreajuste en redes CASCOR; ii) Usen redes CASCOR en la predicción de series de electricidad; iii) comparen el desempeño con redes neuronales tradicionales o modelos estadísticos. El objetivo de este artículo es modelar y predecir el comportamiento de la serie de precios de contratos de electricidad en Colombia, usando redes CASCOR y controlando el sobreajuste con técnicas de regularización.

Palabras clave: pronóstico de series de tiempo, redes cascada correlación, rede neuronales, mercado de electricidad colombiano

Abstract

Prediction of electricity prices is considered a difficult task due to the number and complexity of factors that influence their performance, and their relationships. Neural networks cascade correlation – CASCOR allows to do a constructive learning and it captures better the characteristics of the data; however, it has a high tendency to overfitting. To control overfitting in some areas regularization techniques are used. However, in the literature there are no studies that: i) use regularization techniques to control overfitting in CASCOR networks, ii) use CASCOR networks in predicting of electrical series iii) compare the performance with traditional neural networks or statistical models. The aim of this paper is to model and predict the behavior of the price series of electricity contracts in Colombia, using CASCOR networks and controlling the overfitting by regularization techniques

Keywords: time series forecast, cascade correlation, neural networks, electricity market of Colombia

INTRODUCCIÓN

En Colombia la entrada en vigencia de la Ley de Servicios Públicos Domiciliarios y la Ley Eléctrica ha conducido a restructurar el sector eléctrico, llevándolo a un nuevo esquema de libre competencia. Bajo el nuevo esquema, la operación actual de las unidades generadoras depende de las decisiones descentralizadas de las firmas generadoras, cuya meta es maximizar sus propios beneficios. Todas las firmas compiten para proveer el servicio y el precio es establecido a través de dos mecanismos fundamentales: los contratos bilaterales entre agentes, y la subasta en la bolsa de energía, en la cual los distintos agentes reportan la cantidad de energía disponible y su respectivo precio para la venta, de tal forma que la bolsa fija el precio de venta para los compradores diariamente.

La predicción de precios de bolsa es un problema especialmente complejo [1] debido a la cantidad y complejidad de los factores que influyen en su determinación, tales como: las características físicas del sistema de generación (la ''electricidad'' no puede ser almacenada y su transporte requiere de líneas de transmisión), la influencia de las decisiones de negocio de los distintos agentes, y la regulación. En general, los precios de bolsa manifiestan dichas complejidades a través de sus características que incluyen: pronunciados ciclos estacionales de periodicidad diaria, semanal, mensual y demás; volatilidad variable en el tiempo y regiones de volatilidad similar; fuertes variaciones de año a año y de estación a estación; estructura dinámica de largo plazo; efectos de apalancamiento y respuesta asimétrica de la volatilidad a cambios positivos y negativos; valores extremos; correlaciones de alto orden; cambios estructurales; tendencias locales y reversión en la media; diferentes determinantes para los riesgos de corto, mediano y largo plazo; dependencia de las condiciones de las unidades de generación en el corto plazo y de las inversiones en capacidad, y crecimiento de la demanda en el largo plazo.

Ante la complejidad de la dinámica de los precios de bolsa, la dificultad de su pronóstico y su riesgo implícito, los contratos son un mecanismo de mitigación de riesgo que facilita la operación comercial de los diferentes agentes del mercado. Por una parte, evitan que el comprador se vea sujeto a la variabilidad de los precios en la bolsa, y a precios excepcionalmente altos que ocurren ante la presencia de eventos hidrológicos extremos secos; por otra parte, estabilizan los ingresos del vendedor y lo protegen de precios excepcionalmente bajos que ocurren cuando se presentan eventos hidrológicos extremadamente húmedos. Existen dos tipos de contratos representativos en el mercado eléctrico colombiano: pague–lo–contratado y pague–lo–demandado. El tipo pague–lo–contratado especifica que el comprador se compromete a pagar toda la electricidad contratada, independientemente de si ella fue consumida o no; si se contrató una mayor cantidad de electricidad a la consumida, el excedente puede ser vendido por el comprador en la bolsa de energía. En el tipo pague–lo–demandado, el comprador solo paga la energía efectivamente consumida.

La obtención de pronósticos precisos de los precios de las acciones en el mercado eléctrico es una necesidad fundamental para productores, consumidores y minoristas, toda vez que todas las decisiones operativas y estratégicas de los participantes se basan en el pronóstico de los precios de electricidad [2] . Los productores necesitan predicciones de corto plazo para formular estrategias de comercialización en el mercado de corto plazo, y optimizar su programa de generación; en el mediano plazo, para negociar contratos bilaterales favorables [3] ; y en el largo plazo, para la toma de decisiones relacionadas con el portafolio de activos de generación, la adquisición de nuevas plantas, y el abandono de plantas existentes [4,5] . En consecuencia, es necesario desarrollar modelos de predicción, con un alto rendimiento para series del mercado eléctrico. El objetivo de este artículo es realizar la predicción de la serie de precios promedio mensuales despachados en la bolsa de energía del mercado eléctrico colombiano.

Los modelos de redes neuronales han sido ampliamente usados para representar y predecir series de tiempo con características complejas; específicamente en el mercado de la electricidad se ha informado de su uso en [1] . Sin embargo, la estimación de los parámetros óptimos del modelo en las tradicionales redes neuronales, tipo perceptrón multicapa –MLP– es un problema particularmente difícil, no solo por la complejidad propia del proceso de optimización, sino también porque los parámetros no son únicos. La red neuronal artificial tipo cascada correlación – CASCOR– [6] presenta ventajas conceptuales interesantes en relación con el problema de estimación del MLP. CASCOR está diseñada bajo el esquema de crecimiento en el tamaño de la red o aprendizaje constructivo, donde no es necesario de conocer a priori el número de neuronas ocultas requeridas, de modo que el aprendizaje puede ser más rápido y puede tener una mejor capacidad de generalización de un MLP.

Aunque CASCOR ofrece ventajas para el problema de estimación del tradicional MLP, y ha demostrado ser lo suficientemente robusta como para modelar características complejas, puede sufrir de sobreajuste. Para controlar este problema, en este trabajo, se propone utilizar técnicas de regularización como decaimiento peso, la eliminación de peso y regresión cresta.

En este artículo la predicción de los precios de contratos se hace mediante el uso de redes CASCOR, y se comparan los resultados obtenidos con un modelo de red neuronal MLP y con un modelo estadístico tipo ARIMA, a fin de determinar el mejor modelo de predicción para la serie.

La originalidad y la importancia de este artículo se basa en los siguientes aspectos:

• Aunque existe una amplia experiencia en la predicción de precios de la electricidad en mercados de corto plazo [1] , no existen referencias en la literatura sobre la predicción de precios de contratos con redes CASCOR.

• Existen pocas experiencias reportadas en la literatura comparando el desempeño de las redes CASCOR con otros modelos al pronosticar series del mundo real.

• Ayuda a fomentar el uso de redes CASCOR para el pronóstico de series de precios de la electricidad, incrementando la cantidad de herramientas disponibles.

Este artículo está organizado de la siguiente manera: la sección 1 presenta una descripción general de los modelos de CASCOR en el pronóstico de series de tiempo. En la sección 2 se presenta el protocolo propuesto para el pronóstico de series de tiempo con modelos CASCOR y estrategias de regulación; la aplicación del protocolo a la predicción de los precios de los contratos en el mercado mayorista de electricidad de Colombia y la comparación de los resultados obtenidos con modelos ARIMA y MLP son presentados en la sección 3. Finalmente, las conclusiones se exponen en la sección 4.

1. MODELO CASCADA CORRELACIÓN – CASCOR– PARA EL PRONÓSTICO DE SERIES DE TIEMPO

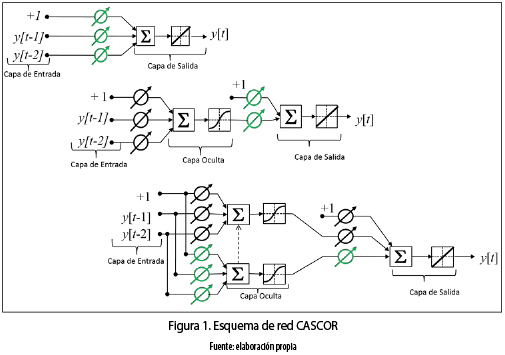
Las redes neuronales CASCOR se caracterizan principalmente por su aprendizaje constructivo, en el cual se comienza con una red mínima, sin neuronas en la capa oculta, luego se adopta un proceso constructivo donde se añade de a una neurona a la vez, evaluando y optimizando en cada paso el error global de la red. En el proceso de adición de neuronas ocultas a la red, cada neurona recibe una nueva conexión sináptica de cada entrada y de cada neurona oculta que la precede. Después de la adición de la nueva neurona oculta, los pesos sinápticos de las entradas se congelan, mientras que sus pesos de salida son optimizados. Este proceso es continuo hasta que se alcanza un rendimiento satisfactorio. La figura 1 muestra el esquema de una red CASCOR; las cajas en las intersecciones de las líneas indican los pesos que se congelan (parámetros ) una vez que se ha añadido una unidad en la capa oculta. Los cruces indican los pesos que son modificados después de la inserción de la neurona.

La red CASCOR combina dos ideas básicas: la primera es la arquitectura en cascada, donde se adiciona de a una neurona oculta, y sus pesos no se cambian una vez ha sido añadida; y el segundo es el aprendizaje incremental o constructivo, que se refiere a cómo las nuevas neuronas ocultas son creadas, donde por cada nueva neurona oculta, el algoritmo maximiza la correlación entre la nueva neurona y el error residual de la red, es decir, las neuronas ocultas se adicionan tratando de reducir el error hasta que su rendimiento es satisfactorio. Esta arquitectura de red presenta varias ventajas respecto a los MLP, entre otras: no es necesario conocer a priori la cantidad de neuronas necesarias en la capa oculta; el aprendizaje de la red puede ser más rápido, y puede tener mejor capacidad de generalización. Este último punto se demostrará experimentalmente en este artículo.

Sin embargo, como en otros modelos, las redes CASCOR pueden adolecer de sobreajuste, debido básicamente a dos causas: la primera está relacionada con el tamaño óptimo de la red; la segunda, con la existencia de datos extremos (outliers) en el conjunto de entrada; esto hace que la varianza de los parámetros de la red sea alta. El sobreajuste se evidencia cuando se produce un error de entrenamiento muy pequeño y un error de validación muy alto. Consecuentemente, si se presentan una o ambas causas, el modelo CASCOR podría sobreajustar los datos y la red tendrá un mal rendimiento en generalización.

1.1 Controlando el sobreajuste de una red CASCOR

En la literatura se han escrito varios trabajos sobre cómo controlar el sobreajuste, tanto para redes neuronales (especialmente MLP) como para otros modelos de aprendizaje de máquina; entre estos se encuentran: [7–12] . En los MLP el problema de sobreajuste es controlado, principalmente, mediante tres estrategias de regularización: descomposición de pesos (weightdecay) propuesta por [8] , eliminación de pesos (weight elimination) por [13] (ambas son estrategias de reducción y son descritas en [9] ), y regresión en cadena (ridge regression) propuesta por [14] . Si bien, la efectividad de las estrategias de regularización mencionadas ha sido probada en diferentes ámbitos, no se ha evaluado su desempeño en redes CASCOR.

1.1.1 Descomposición de pesos (WD)

La idea principal de la regularización es encontrar una solución estable en los pesos de los parámetros de la red neuronal usando algún tipo de penalización en la función objetivo, cuando esta se desvía de lo que se pretende alcanzar. Las redes de gran tamaño son propensas a aprender las particularidades o ruido presentes en los datos de entrenamiento y a incurrir en el problema bien conocido del sobreajuste [15] . Para solucionarlo es necesario reducir el tamaño de la red mientras se mantiene su buen rendimiento; la idea central es obtener una red con un tamaño óptimo, menos propensa a aprender el ruido en los datos de entrenamiento y a incurrir en el sobreajuste, y por ende, que generalice con mayor precisión en un tiempo computacional menor que una red de mayor tamaño.

La función general de regularización está dada por la minimización del riesgo total [15] (ecuación 1):

donde,

• ξ _s(W) se conoce como la medida estándar de rendimiento, acostumbra medidas de error de ajuste, tales como el MSE o el SSE;

• ξ _c(w) corresponde al término de regularización, que puede asumir diferentes formas funcionales;

• λ es el parámetro o factor de regularización que controla el nivel de incidencia de ξ _c(w) sobre el entrenamiento de la red.

La descomposición de pesos es una de las estrategias de regularización más utilizadas en la literatura [16] , dado que su implementación es computacionalmente sencilla, no depende de parámetros adicionales y permite mejorar la capacidad de generalización de la red neuronal. Esta técnica fue propuesta por [8] y también trabajada por [17] bajo el nombre de regresión de borde (ridge regression).

El procedimiento de descomposición de pesos opera sobre algunos pesos de la red forzándolos a tomar valores cercanos a cero y permitiendo a otros conservar valores relativamente altos. Esta discriminación permite agrupar los pesos de la red en pesos que tienen poca o ninguna influencia sobre el modelo, y pesos que tienen influencia sobre el modelo, llamados pesos de exceso. Para esta estrategia la penalización se define según la ecuación 2:

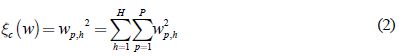
w_p,h son los pesos de la entrada p a la neurona h, (pesos entre la capa de entrada y la oculta).

1.1.2 Eliminación de pesos (WE)

Este método de regularización descrito por [13] define la penalización de complejidad como se ilustra en la ecuación 3:

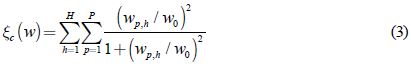
donde, w₀ es un parámetro predefinido, el cual se elige según el criterio de una persona experta. El término w_p,h/w₀ hace que la penalización compleja tenga un comportamiento simétrico. Además, cuando 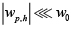, 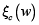tiende a cero, es decir, para el aprendizaje el peso sináptico w_p,h es poco fiable, por consiguiente puede ser eliminado de la red. Mientras que cuando 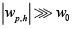, 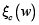tiende a uno, entonces el peso w_p,h es importante para el proceso de aprendizaje. En conclusión, este método busca los pesos que tienen una influencia significativa sobre la red, y descarta los demás.

1.1.3 Regresión en cadena (RR)

Los parámetros de un perceptrón multicapa son estimados utilizando el principio de máxima verosimilitud de los residuales, el cual equivale a la minimización de la función de costo que es definida usualmente como el error cuadrático medio. Sin embargo, la estimación por mínimos cuadrados no es robusta frente a valores extremos o atípicos (outliers) presentes en los datos de entrada. Por lo tanto, si el conjunto de entrada posee valores extremos es más apropiado usar métodos de regresión robusta, como regresión en cadena.

La regresión en cadena, propuesta [14] , realiza la búsqueda de estimadores que pueden ser sesgados con menor error cuadrático medio que el mínimo insesgado, es decir, es posible encontrar estimadores mejores que los hallados con mínimos cuadrados. La idea central de esta estrategia es controlar la varianza de los parámetros buscando el equilibrio entre sesgo y varianza (bias variance trade–off).

2. PROTOCOLO PARA LA ESPECIFICACIÓN DE REDES CASCOR Y EL CONTROL DEL SOBREAJUSTE

A continuación se presenta el protocolo seguido para la especificación de redes CASCOR en la predicción de series de tiempo.

2.1 Exploración preliminar de la serie de tiempo y preprocesamiento

Como paso inicial en la especificación del modelo de la series de tiempo, es necesario, un entendimiento previo de la serie y evaluar si se requiere un preprocesamiento. A menudo, se recomienda tomar el logaritmo natural de la serie si esta es heterocedástica, es decir, no tiene varianza constante. Asimismo, la exploración visual del comportamiento de la serie, es una herramienta útil para identificar componentes regulares como tendencias y patrones estacionales, e irregulares como outliers, que podrían, igualmente, requerir un proceso previo.

2.2 Selección de neuronas ocultas y entradas, y regularización de redes CASCOR

La selección de la cantidad de neuronas en la capa oculta de la red se hace basado en el aprendizaje incremental de la arquitectura de las redes CASCOR. A pesar de que la red misma determina su tamaño y topología, esta pueden adolecer de sobreajuste; para controlar este problema se utilizan la regularización de los pesos entre la capa de entrada y la oculta con las estrategias de descomposición o eliminación de pesos, y los pesos entre la capa oculta y la de salida con regresión en cadena. En este orden de ideas, es posible tener los siguientes esquemas de regularización: i) regularizar con eliminación de pesos; ii) regularizar con descomposición de pesos; iii) regularizar con regresión en cadena; iv) regularización combinada con eliminación de pesos y regresión en cadena; o v) regularización combinada con descomposición de pesos y regresión en cadena.

La selección de las entradas a la red (rezagos de la variable y_t) es controlada, implícitamente, mediante la estrategia de regularización de eliminación de pesos; una anulación del peso w_p,h mediante la estrategia implica que la entrada y_{t– p} asociada a dicho peso no será tenida en cuenta en la red; mientras que si el peso w_p,h es cercano a uno, este es importante para el proceso de aprendizaje y, por ende, la entrada y_{t– p} también lo será. Similarmente, se controlan implícitamente las entradas con la estrategia de descomposición de pesos; si la estrategia fuerza a que w_p,h tome un valor cercano a cero, este peso tendrá poca importancia en la red y, por tanto, el rezago y_{t– p} tampoco la tendrá; si por el contrario, w_p,h es forzado a tomar un valor relativamente alto, este peso tendrá importancia en la red y por tanto el rezago y_{t– p} también la tendrá.

2.3 Optimización de los parámetros de la red CASCOR

Una vez seleccionada una arquitectura adecuada, se requiere optimizar los parámetros de la red CASCOR. En este artículo se hace uso del algoritmo ConRprop [18] , el cual es una técnica que permite encontrar modelos con mejor capacidad de generalización que los obtenidos con los MLP optimizados con otras técnicas. Para el entrenamiento de la red se utiliza el 80 % de los datos de la serie, y para su validación el 20 % restante.

2.4 Análisis de resultados

La etapa final del protocolo es la evaluación y comparación de los resultados obtenidos con el uso de cada estrategia de regularización. La comparación de los resultados se basa en la bondad de ajuste de los modelos medida con la sumatoria del error cuadrático (SSE) tanto en entrenamiento como en pronóstico (validación). Igualmente, como ejercicio de comparación, se construyeron modelos MLP y ARIMA para la serie de tiempo estudiada.

3. PRONÓSTICO DEL PRECIO PROMEDIO MENSUAL DE LOS CONTRATOS DESPACHADOS EN LA BOLSA DE ENERGÍA DE COLOMBIA

3.1 Exploración preliminar y preprocesamiento

Los datos con los cuales se elaboró este estudio corresponden al logaritmo natural de la serie de precios mensuales promedio de los contratos despachados en la bolsa del mercado mayorista de electricidad en Colombia, expresada en $/kWh, entre enero de 1997 (1997:01) y octubre de 2009 (2009:10), los cuales están disponibles en el sistema Neón (véase figura 2). La serie presenta una tendencia creciente de largo plazo desde 1997:1 hasta el primer semestre del 2003; durante ese mismo intervalo de tiempo se evidencia una componente cíclica de periodicidad anual de amplitud variable, explicada, posiblemente, por el ciclo invierno–verano. La mayor amplitud de la componente periódica coincide con el fenómeno de El Niño ocurrido entre los años 1997 y 1998; esta componente cíclica, aunque no con una amplitud tan marcada, permanece hasta principios del año 2004. Desde el año 2003, se presenta una tendencia ligeramente descendente que finaliza en algún momento del primer semestre del año 2006. Se evidencia en este momento del tiempo, un cambio estructural en la serie, tanto en su tendencia como en su componente cíclica; por una parte, se recuperan los niveles de crecimiento que caracterizaron los años 2000, 2001 y 2002; mientras que por la otra, se presenta nuevamente un ciclo estacional de periodo anual, cuyo nivel más alto coincide con la estación de verano.

La serie consta de 154 datos, de los cuales los primeros 130 (1997:01 al 2007:10) son utilizados para la estimación de los parámetros de los modelos de la Tabla 1. Sumatoria del error cuadrático (SSE) al pronosticar la serie con diferentes modelos. Para comprobar la capacidad de generalización de los modelos para distintos horizontes de tiempo, se usan 2 muestra de pronóstico: la primera, consta de 12 datos (del 2007:11 al 2008:10), correspondiente a un año; y la segunda, correspondiente a dos años, de 24 observaciones (entre 2006:7 y 2009:10).

3.2 Selección de neuronas ocultas, entradas, y regularización

Tal como se estableció en el protocolo descrito en la sección 2, se usarán diferentes esquemas de regularización para realizar el pronóstico de la serie:

i. EP, red CASCOR regularizada con eliminación de pesos.

ii. DP, red CASCOR regularizada con descomposición de pesos.

iii. RC, red CASCOR regularizada con regresión en cadena.

iv. EP+RC, red CASCOR regularizada con eliminación de pesos y regresión en cadena.

v. DP+RC, red CASCOR regularizada con descomposición de pesos y regresión en cadena.

Para la regularización por descomposición de pesos se toma λ =0.0001, y para eliminación de pesos λ =0.0001 y w₀=100.

3.3 Resultados obtenidos y discusión

Para la serie estudiada se estimaron los modelos de la Tabla 1. Sumatoria del error cuadrático (SSE) al pronosticar la serie con diferentes modelos, con los cuales se realizó el pronóstico en un horizonte de uno y dos años, es decir, 12 y 24 meses, respectivamente. En la tabla 1, se presenta la bondad de ajuste de cada estrategia de regularización.

Para evaluar la capacidad de predicción de las redes CASCOR respecto a otros modelos, se realiza la comparación respecto a un MLP; e ilustrativamente se presenta un modelo auto–regresivo integrado de promedios móviles (ARIMA). El modelo MLP fue estimado para diferentes conjuntos de rezagos, y se seleccionaron los mejores modelos con menor error. La arquitectura del MLP consta de una capa de entrada con una neurona por cada uno de los rezagos considerados, una capa oculta con 5 neuronas (la misma cantidad alcanzada por los modelos CASCOR), y una capa de salida; los nodos de la capa oculta se activan con la función sigmoidea bipolar, mientras que en la capa de salida, con la función identidad; los resultados se presentan, igualmente, en la tabla 1. Mientras que el modelo ARIMA se obtiene utilizando la función auto.arima() implementada en R del paquete forecast de [19] , la cual busca el mejor modelo ARIMA para una serie de tiempo univariada; el modelo encontrado fue ARIMA(0,1,0)(2,0,2) [12] ; el resultado del pronóstico se presenta también en la tabla 1 y se destaca que todos los modelos CASCOR regularizados alcanzan un error inferior al de la red CASCOR correspondiente sin regularizar.

Los resultados de la tabla 1 muestran que en los modelos con tres rezagos, el CASCOR–EP+RC–1 es el que obtiene el menor error en entrenamiento y de pronóstico a 2 años, mientras que con el CASCOR–RC–1 se obtiene el menor de pronóstico a un año; no obstante, el error de pronóstico a un año del modelo CASCOR–EP+RC–1 es tan solo 4 % mayor que el menor en modelos de 3 rezagos. Además, todos los modelos CASCOR de tres rezagos tienen mejor generalización que el MLP–1; asimismo, los modelos CASCOR–DP–1 y CASCOR–EP+RC–1 son superiores al modelo ARIMA, tanto en entrenamiento como en pronóstico; los demás solo son superiores en predicción. Al aumentar la cantidad de rezagos, a seis y a trece, se observa que los modelos CASCOR siguen siendo superiores al respectivo MLP, incluso, también lo son respecto al ARIMA.

Cuando se tienen 6 rezagos, los modelos CASCOR–EP+RC–2 y CASCOR–RC–2 continúan siendo los mejores en entrenamiento y pronóstico a un año, respectivamente; pero ahora CASCOR–RC–2 también lo es en pronóstico a 2 años. La diferencia de CASCOR–RC–2 respecto a CASCOR–EP+RC–2 en entrenamiento es del 33 %; mientras que de CASCOR–EP+RC–2 respecto a CASCOR–RC–2 en pronóstico es de 8.42 % y 8.13 %, a uno y dos años, respectivamente. La diferencia entre los dos modelos es más amplia en entrenamiento; por tanto, en este caso puede ser más apropiado el modelo CASCOR–EP+RC–2. Por otro lado, la diferencia de CASCOR–EP+RC–2 respecto a CASCOR–DP+RC–2 es de –2.34 %, 2.11 % y 3.13 % en entrenamiento, pronóstico a uno y dos años, respectivamente; el modelo CASCOR–DP+RC–2 también se perfila como uno conveniente para modelar la serie. Se destaca que los modelos regularizados en ambas capas alcanzan un menor error de entrenamiento que los demás; pero en pronóstico el menor error lo alcanza el modelo que es solo regularizado en la capa de salida.

El hecho de aumentar a 13 rezagos, presenta al modelo CASCOR–DP+RC–3 como el mejor de todos; este está regularizado entre la capa de entrada y la oculta con descomposición de pesos, y entre la oculta y la de salida con regresión en cadena, es decir, en este modelo se controla el sobreajuste, mientras que los errores del modelo CASCOR–3, que no tiene ningún tipo de estrategia de regularización, son notoriamente más grandes que los alcanzados por CASCOR–DP+RC–3.

En general, para esta serie, los modelos CASCOR regularizados completamente – entre capa de entrada y oculta, y entre oculta y salida– alcanzan mejores errores que la mayoría de modelos regularizados solo con una técnica; además, los regularizados completamente son más apropiados para realizar el pronóstico, dado que controlan en gran medida las causas del sobreajuste.

4. CONCLUSIONES

Desde la literatura se puede evidenciar un creciente interés por la realización de modelos de redes neuronales que conduzcan a resultados cada vez más acertados en el pronóstico, favorecido por sus características de adaptabilidad, no linealidad y habilidad para aprender comportamientos desconocidos. Los desarrollos han conducido al uso de técnicas que permiten ganancias notorias en el ajuste, tal es el caso de las redes tipo cascada correlación. Si bien, el uso de redes tipo CASCOR ha demostrado ser una herramienta en el pronóstico de series de tiempo, toda vez que permite un mejor ajuste que otras técnicas, las redes que usan CASCOR presentan una alta tendencia al sobreajuste; por lo tanto, en este artículo se trabajó en pro de corregir esta deficiencia mediante el uso de tres técnicas diferentes de regularización.

La eficiencia del control del sobreajuste con las técnicas de eliminación de pesos, descomposición de pesos y regresión en cadena, fue evidenciada a través del modelado y pronóstico de la serie de precios promedio mensual de los contratos despachados en la bolsa de energía de Colombia. Para los horizontes de pronóstico de 12 y 24 meses, los resultados indican que las redes CASCOR regularizadas completamente pronostican de manera más precisa que los MLP, que el modelo ARIMA y que las mismas CASCOR sin regularizar; y por tanto, el protocolo de selección propuesto permite encontrar modelos con mejor capacidad de generalización que otras propuestas en la literatura.

REFERENCIAS

[1] J. D. Velásquez, I. Dyner, and R. C. Sousa, ''¿ Por qué es tan difícil obtener buenos pronósticos de los precios de la electricidad en mercados competitivos?'', Cuadernos de Administración, n.° 20, p. 259– 282, 2007.

[2] Y. Hong and C. Lee, ''Aneuro–fuzzy price forecasting approach in deregulated electricitymarkets'', Electric Power Systems Research, n.° 73, p. 151– 157, 2005.

[3] A. Conejo, J. Contreras, R. Espínosa, and M. Plazas, ''Forecasting electricity prices for a day–ahead pool–based electric energy market'', International Journal of Forecasting, n.° 21, p. 435– 462, 2005.

[4] X. Lu, Z. Dong, and X. Li, ''Electricity market price spike forecast with data mining techniques'', Electric Power Systems Research, vol. 73, n.° 1, p. 19– 29, 2005.

[5] A. Angelus, ''Electricity price forecasting in deregulated markets'', The Electricity Journal , vol. 13, n.° 4, pp. 32–41, 2001.

[6] S. E. Fahlman and C. Lebiere, ''The Cascade–Correlation Learning Architecture'', Advances in Neural Information Processing Systems , vol. 2, pp. 524–532, 1990.

[7] E. B. Baum and D. Haussler, ''What size net gives valid generalization?'', Neural Computation, vol. 1, n.° 1, p. 151– 160, 1989.

[8] G. E. Hinton, ''Connectionist learning procedures'', Artificial Intelligence, n.° 40, p. 185– 243, 1989.

[9] A. K. Palit and D. Popovic, Computational Intelligence in Time Series Forecasting. London: Springer, 2005.

[10] Q. Yu, Y. Miche, E. Eirola, and M. van Heeswijk, ''Regularized extreme learning machine for regression with missing data'', Neurocomputing, vol. 102, n.° 15, pp. 45–51, Feb. 2013.

[11] O. Ludwig, U. Nunes, and R. Araujo, ''Eigenvalue decay: A new method for neural network regularization'', Neurocomputing, vol. 124, n.° 26, pp. 33–42, 2014.

[12] X. Dutoit, et al., ''Pruning and Regularization in Reservoir Computing'', Neurocomputing, n.° 72, pp. 1534–1546, 2009.

[13] A. S. Weigend, D. E. Rumelhart, and B. A. Huberman, ''Generalization by weight–elimination with application to forecasting'', in Advances in Neural Information Processing Systems, R. P. Lippmann, J. E. Moody, and D. S. Touretzky, Eds. San Mateo, CA, USA: Morgan Kaufmann Publishers Inc., 1991, vol. 3, p. 875– 882, ISBN:1–55860–184–8 .

[14] A. E. Hoerl and R. W. Kennard, ''Ridge Regression: Biased Estimation for Nonorthogonal Problems'', Technometrics., vol. 12, n.° 1, p. 55– 67, 1970.

[15] S. Haykin, Neural Networks: A Comprehensive Foundation. New Jersey: Prentice Hall, 1999.

[16] C. S. Leung, H. J. Wang, and J. Sum, ''On the selection of weight decay parameter for faulty networks'', IEEE Transactions on Neural Networks , vol. 8, n.° 21, pp. 1232–1244, 2010.

[17] C. M. Bishop, Neural Networks for Pattern Recognition. Oxford: Oxford University Press, 1995.

[18] F. A. Villa, J. D. Velásques, and P. Jaramillo, ''Conrprop: un algoritmo para la optimización de funciones no lineales con restricciones'', Revista Facultad de Ingeniería Universidad de Antioquia, n.° 50, pp. 188–194, 2009.

[19] R. J. Hyndman and Y. Khandakar, ''Automatic time series forecasting: The forecast package for R'', Journal of Statistical Software, vol. 26, n.° 3, 2008.