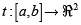 con
con 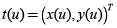 para
para 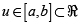 , la medición de la curvatura de una superficie depende de cuánto se desvían dos líneas geodésicas que tienen sus vectores tangentes inicialmente paralelos.
, la medición de la curvatura de una superficie depende de cuánto se desvían dos líneas geodésicas que tienen sus vectores tangentes inicialmente paralelos.ARTÍCULOS
Metodología de remallado basado en la curvatura y orientado a modelos 3D del rostro humano*
Curvature–based remeshing methodology oriented to human face 3D models
Marco Jinete**; Flavio Prieto***; Augusto Salazar****
** Magíster, Universidad Nacional de Colombia Sede Bogotá. Carrera 30 N.° 45–03, Bogotá, Colombia. Teléfono: (1) 316 5000 Ext. 14103. E–mail: majineteg@unal.edu.co.
*** Profesor titular. Departamento de Ingeniería Mecánica y Mecatrónica. Universidad Nacional de Colombia Sede Bogotá. Carrera 30 N.° 45–03, Bogotá, Colombia. Teléfono: (1) 316 5000 Ext. 14103. E–mail: faprietoo@unal.edu.co
**** Docente, Grupo de Automática y Electrónica, Instituto Tecnológico Metropolitano. Calle 54A # 1–30. Calle 73 N.° 76A – 354 Vía al Volador, Medellín, Colombia. Teléfono: (4) 440 5100. E–mail: aesalazar@unal.edu.co
Recibido: 10/02/2014
Aceptado: 12/12/2014
Resumen
Las técnicas de remallado buscan modificar la malla de entrada para adaptarla a la aplicación específica. En este trabajo se propone una metodología de remallado especializada en el rostro humano, cuyo propósito es reducir el número de caras y vértices que requiere la malla, manteniendo las características propias de la anatomía humana. Para lograr esto se utiliza la información de curvatura, la cual destaca la anisotropía intrínseca en la geometría natural o en la geometría de origen humano. Como resultado se obtuvieron mallas anisotrópicas poligonales, compuestas principalmente por cuadriláteros, con menos del 50% de los puntos y caras de la malla inicial, que mantienen las características anatómicas para modelos del rostro en expresión neutra, o con expresiones de alegría, enojo, repugnancia, miedo, sorpresa y tristeza. La metodología se validó con los modelos presentes en la base de datos BU–3DFE, y se comparó la calidad de los resultados obtenidos contra el remallado que se logra con la técnica de simplificación basada en quadric error metrics.
Palabras clave: remallado, líneas de curvatura, antropometría facial.
Abstract
Remeshing techniques seek to modify a mesh in order to adapt it to an specific application. This work proposes a remeshing methodology specialized in the human face, whose purpose is to reduce the number of faces and vertices that requires the mesh, keeping the characteristics of the human anatomy. Curvature information that highlights the intrinsic anisotropy of natural geometry or geometry of human origin is used to accomplish this. Results were polygonal anisotropic meshes, composed mainly of quadrilaterals, with less than 50% of the points and faces of the initial mesh, that maintain the anatomical features for models of the face in a neutral expression, or expressions of happiness, disgust, fear, angry, surprise, and sadness. The methodology was validated with models from the BU–3DFE database, and the quality of the obtained results were evaluated against the remeshing achieved when a technique of simplification based on quadric error metrics is used.
Keywords: remeshing, curvature lines, facial antropometry.
INTRODUCCIÓN
El remallado es una técnica de modelado geométrico, que busca mejorar la calidad de una malla 3D o representación geométrica de un objeto (modelo 3D). Aunque no se tiene una definición universalmente aceptada, una posible definición es la siguiente: ''dada una malla 3D, calcular otra malla, cuyos elementos cumplan algunos requisitos de calidad, aproximando la entrada de forma aceptable según la aplicación'' [1] . El término calidad puede referirse a toma de muestras, clasificación, regularidad, tamaño o forma de los elementos, todas dirigidas a mejorar los problemas de la malla inicial.
En los últimos años se han desarrollado diversos algoritmos que abordan el remallado, los cuales normalmente se clasifican según su objetivo final, por ejemplo: i) mejorar la estructura de las mallas (a lo largo del texto se usará el término malla para referirse a malla 3D, y el término modelo para referirse a una malla 3D que represente geométricamente un objeto o rostro humano), para que sean completamente regulares [2] , o semirregulares [3] ; ii) buscar la compatibilidad de dos o más modelos [4, 5] ; iii) mejorar la calidad de los componentes [6] ; iv) realzar alguna característica propia del modelo [7] ; v) basados en el manejo del error buscando un equilibrio entre complejidad y exactitud geométrica [8, 9] . Dichas técnicas buscan modificar la malla inicial para acomodarla a las necesidades de la aplicación específica.
Los métodos de remallado basados en la explotación y análisis del vector de curvatura de la superficie, para mejorar la estructura y la eficiencia de la malla, han demostrado que es posible reducir la complejidad de la misma, conservando su forma, sin necesidad de generar un modelo isotrópico regular [10–12, 9].
En este trabajo, se desarrolla una metodología de remallado anisotrópico, basada en el manejo del error y especializada en la geometría del rostro para la caracterización de su morfología y dinámica, simplificando el tamaño y la complejidad de las mallas iniciales que representan el rostro humano. El eje de generación del remallado son los vectores de curvatura de la superficie. Las complejas características dinámicas que se encuentran en las superficies del rostro humano hacen que el proceso de remallado no sea fácil, y enfocarse solo en mejorar la malla puede ocasionar pérdida de información importante.
Esta aplicación puede ser orientada al mejoramiento de la malla 3D de modelos específicos, por ejemplo para malla de modelos de rostro humano, como en [2] , donde se busca obtener un modelo regular para mejorar el proceso de visualización y reconocimiento. Debido a las características anisotrópicas del mallado del rostro humano, la técnica propuesta se ajusta muy bien para modelarlo, con lo que se podría conseguir mallas especializadas en la geometría del rostro, tanto en rostros neutros (sin expresión definida), como en rostros con expresiones.
1. METODOLOGÍA DE REMALLADO
La técnica de remallado presentada se enfoca en ajustar la malla a las características propias de la superficie. Ella está motivada en la idea de alinear los bordes de las características más generales en toda la superficie. Como resultado se obtiene una malla poligonal que refleja la simetría de los puntos de la forma de entrada, con segmentos de recta en lugar de nubes de puntos.
El algoritmo se puede agrupar en tres etapas a saber: i) estimación de un tensor de curvatura 3D por vértice; ii) construcción de una red de líneas de curvatura para el remuestreo de la malla; y iii) generación de la nueva malla.
1.1. Cálculo del tensor de curvatura
Una curva se puede representar de forma paramétrica con una función vectorial v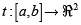 con
con 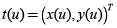 para
para 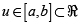 , la medición de la curvatura de una superficie depende de cuánto se desvían dos líneas geodésicas que tienen sus vectores tangentes inicialmente paralelos.
, la medición de la curvatura de una superficie depende de cuánto se desvían dos líneas geodésicas que tienen sus vectores tangentes inicialmente paralelos.
Gracias a la naturaleza lineal a tramos de la malla de entrada y con el fin de obtener un campo tensorial continuo en toda la superficie, se debe construir un campo de tensor de curvatura lineal a tramos, para estimar la curvatura del tensor en cada vértice e interpolar estos valores linealmente en los vértices de cada triángulo. Sin embargo, calcular en el nivel local el tensor de curvatura no es un procedimiento trivial, por lo que se define el tensor de curvatura en cada punto a lo largo del borde [13] .
Esta línea de tensores puede integrarse sobre una región arbitraria B (figura 1), y sumarse sus componentes en la expresión:
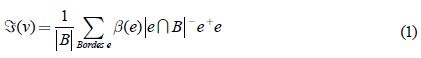
donde v es un vértice arbitrario de la malla, |B| es la superficie alrededor de v sobre la que el tensor es estimado 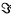 , β (e)es el signo del ángulo entre la normal y las dos orientaciones de los triángulos incidentes al borde
, β (e)es el signo del ángulo entre la normal y las dos orientaciones de los triángulos incidentes al borde 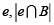 es la longitud de
es la longitud de 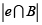 , y – e es el vector unitario en la misma dirección de e.
, y – e es el vector unitario en la misma dirección de e.
El tensor se evalúa en todos los vértices v, dentro de una zona B que se aproxima a un disco geodésico alrededor de este vértice. La normal de cada vértice puede ser estimada por el vector propio de 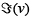 asociado con el valor propio de mínima magnitud. Los dos valores propios principales kmin y kmax (figura 2) son estimados de la curvatura principal en v. Una etapa preliminar a la generación de las líneas de curvatura es un suavizado (figura 2(b)), el cual se realiza promediando las direcciones de los vectores de curvatura dentro de un anillo centrado en cada vértice.
asociado con el valor propio de mínima magnitud. Los dos valores propios principales kmin y kmax (figura 2) son estimados de la curvatura principal en v. Una etapa preliminar a la generación de las líneas de curvatura es un suavizado (figura 2(b)), el cual se realiza promediando las direcciones de los vectores de curvatura dentro de un anillo centrado en cada vértice.
1.2. Generación de las líneas de curvatura
Una línea de curvatura se define como una curva sobre la superficie, cuyos puntos tienen un vector tangente colineal con los vectores directores de curvatura de la superficie. La técnica desarrollada por [11] permite determinar la línea de curvatura y, además, logra la integración de estas líneas triángulo a triángulo. La técnica en este trabajo se puede desarrollar en los siguientes pasos: i) parametrización local; ii) representación en coordenadas baricéntricas; iii) vector director de curvatura; iv) generación local de la línea; y v) terminación de la línea de curvatura.
1.2.1. Parametrización local
En la técnica propuesta en este trabajo se utiliza una parametrización local, en la cual no se requiere calcular la parametrización total de la malla, sino que se realiza la parametrización de los triángulos que se estudian localmente para la generación de cada segmento de la línea de curvatura [14] . Esta parametrización inicia con la selección aleatoria de un triángulo que será el contenedor de la semilla de la línea de curvatura; se realiza una parametrización isométrica del triángulo mapeando sus vértices en el plano paramétrico (u,v); este mapeo se logra aplanando el triángulo de 3D a 2D, conservando sus dimensiones originales. Dentro del plano paramétrico (u,v), se utilizan coordenadas baricéntricas, para que todos los puntos identificados de la línea se puedan utilizar indistintamente en el triángulo paramétrico y el triángulo en la superficie en 3D.
1.2.2. Representación en coordenadas baricéntricas
Si se considera un triángulo en el plano 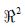 de vértices A(Xa, ya), B(xb, yb), C(xc, yc), entonces cualquier punto interior del triángulo P(x,y), puede ser representado por tres coordenadas baricéntricas (λ 1, λ 2, λ 3), donde λ 1 + λ 2 + λ 3 = 1, cuyos valores deben pertenecer al rango 0 ≤ λ 1 + λ 2 + λ 3 < 1. Las tres componentes baricéntricas se obtienen de la relación de las áreas de los triángulos internos A1, A2 y A3 con el área total AT, como: λ 1 = A1/AT, λ 2 = A2/AT y λ 3 = A3/AT (figura 3(b)). Si λ 1 + λ 2 + λ 3 ≠ 1 el punto no está dentro del triángulo.
de vértices A(Xa, ya), B(xb, yb), C(xc, yc), entonces cualquier punto interior del triángulo P(x,y), puede ser representado por tres coordenadas baricéntricas (λ 1, λ 2, λ 3), donde λ 1 + λ 2 + λ 3 = 1, cuyos valores deben pertenecer al rango 0 ≤ λ 1 + λ 2 + λ 3 < 1. Las tres componentes baricéntricas se obtienen de la relación de las áreas de los triángulos internos A1, A2 y A3 con el área total AT, como: λ 1 = A1/AT, λ 2 = A2/AT y λ 3 = A3/AT (figura 3(b)). Si λ 1 + λ 2 + λ 3 ≠ 1 el punto no está dentro del triángulo.
1.2.3. Vector director de curvatura
Con el fin de determinar la dirección que se debe seguir dentro del triángulo, inicialmente se identifican los vectores de curvatura en cada punto del triángulo, lo que ya se obtuvo, por que se tienen los vectores de curvatura de cada vértice de la malla, y los puntos que componen estos triángulos siempre son vértices de la malla. Posteriormente, se calcula la dirección del vector de curvatura, que determina la dirección de la línea en el triángulo inicial; esto se logra calculando la dirección promedio de los vectores de curvatura que componen el triángulo (figura 5(a)). Este proceso se realiza con los vectores de curvatura máximos y mínimos, y cada uno corresponde a la dirección de la línea de curvatura máxima y mínima, respectivamente. Este nuevo vector de curvatura promedio se traslada al punto inicial de la línea de curvatura que, para este primer triángulo, se ubica en el centro del triángulo (figura 4(c)), con ayuda de las coordenadas baricéntricas, ya que el punto central del triángulo se encuentra cuando λ 1 = λ 2 = λ 3 = 1/3.
1.2.4. Generación local de la línea
Como ya se calculó la dirección de los vectores de curvatura que guiarán la línea de curvatura, se procede a dibujar la línea de curvatura siguiendo esta dirección, estirando el vector unitario en pequeños incrementos, para luego evaluar si el punto final de la línea se encuentra o no dentro del triángulo. La dirección es la misma mientras el punto final de la línea esté dentro del triángulo (figura 5(a)). Cuando se identifica que el punto final, luego de la elongación, está fuera del triángulo, se procede a identificar cuál de los triángulos vecinos al triángulo actual es el que contiene el punto final del segmento de línea calculado hasta el momento. Se llaman triángulos vecinos a los triángulos que comparten al menos un punto. Para identificar en qué triángulo se encuentra el punto final del segmento, se recurre nuevamente a las coordenadas baricéntricas; el procedimiento es pasar este punto a coordenadas baricéntricas para cada uno de los triángulos vecinos y cuando λ 1 + λ 2 + λ 3 = 1, quiere decir que el punto está en este triángulo.
El siguiente paso consiste en calcular la nueva dirección de la línea de curvatura; para ello se requiere nuevamente el cálculo de los vectores de curvatura promedio, pero ahora se calculan con base en los puntos que componen este nuevo triángulo, el cual contiene el punto final del primer segmento de línea. Teniendo esta nueva dirección promedio, el proceso es el mismo que para el triángulo inicial: se estira el vector en dirección promedio hasta que el punto final esté fuera del triángulo (figura 5(b)); la única diferencia es que no se traslada el vector de curvatura al punto central del triángulo, sino al punto final del segmento anterior. Este proceso se repite (figuras 5(c) y 5(d)), hasta que alguno de los criterios de terminación de línea se cumpla.
1.2.5. Terminación de la línea de curvatura
La línea puede terminar por algunas de las siguientes dos causas. Primero, si no se encuentra ningún triángulo vecino al cual pertenezca el punto final del segmento; esto se presenta cuando la malla terminó (extremo de la malla). Segundo, cuando el promedio de las direcciones que componen la línea de curvatura y la dirección para el nuevo segmento supera un ángulo de π /4. Esta condición se requiere para evitar que las líneas de curvatura tengan cambios bruscos. Un resultado de este proceso se ilustra en la figura 6, donde las líneas azules son las líneas formadas a partir de los vectores de curvatura máximos, y las líneas verdes son formadas a partir de los vectores de curvatura mínimos.
1.3. Obtención del remallado
1.3.1. Vértices de la malla final
Los vértices de la malla final se definen como los cruces entre las líneas de curvatura máximas y mínimas, producto de la ortogonalidad que existe entre ellas (figura 7).
Los cruces entre dos segmentos de línea en 3D difícilmente se encuentran en el mismo punto; por esto se implementó un procedimiento de cálculo de puntos cercanos, estableciendo un umbral mínimo para determinar si los puntos se están cruzando o no.
El procedimiento consta de los siguientes pasos:
• Determinar las líneas vecinas: identificando los triángulos que pertenecen a una línea, los que se obtienen en el momento de la generación de las líneas de curvatura, ya que para su generación se realiza un recorrido triángulo a triángulo.
• Calcular las distancias punto a punto entre líneas vecinas: tomando un punto inicial de una línea de curvatura máxima, se identifica el triángulo al cual pertenece e inicia el cálculo de distancia euclidea (en tres dimensiones) con los puntos de líneas vecinas.
• Asignar un umbral: teniendo las distancias calculadas se debe identificar, según la escala del modelo, un umbral que determine cruce o no. Este valor debe ser pequeño, ya que en caso contrario se puede asignar más de un vértice en puntos cercanos al cruce.
• Almacenar de nuevos vértices: luego de identificados, los cruces se almacenan para continuar con el proceso de creación del modelo.
1.3.2. Generación de la malla final
Como se evidencia en la figura 8, los puntos de cruce o puntos generadores, que resultan del procedimiento anterior, tienen una distribución que permite la generación de polígonos; por esta razón la malla final será el resultado de la formación de caras poligonales; con lo que se busca reducir el número de caras. El último paso del algoritmo es la generación de la malla resultante, con base en los puntos clave del remallado, calculados en el proceso anterior. Para esto se creó una malla formada por una cuadrícula centrada en el origen, con la cual se busca agilizar el proceso de generación de la malla teniendo la distribución de vértices por cara. La malla con la cuadrícula debe estar alineada con los puntos del modelo, por lo que se debe trasladar todo el conjunto de puntos clave del remallado al punto origen de la cuadrícula, lo que se logra calculando su centroide y aplicando una transformación que lo lleve al punto de origen (0, 0, 0).
Luego de la alineación, cada vértice de la cuadrícula es asignado a un punto de los puntos clave del remallado, de tal forma que se conserve la malla, y los vértices de esta sean los puntos del remallado; con esto se genera una nueva malla donde los vértices son los puntos generadores. Este proceso consiste en cambiar cada punto de la cuadrícula, por el punto del remallado con la mínima distancia, conservando la asignación original de las caras realizada en la creación de la malla basada en la cuadrícula. La cuadrícula tiene muchos más puntos que el remallado (lo que garantiza que se conserve la anisotropía del modelo). El proceso termina con la eliminación de los vértices duplicados que se generan por la asignación de más de un punto de la cuadrícula a un punto generador.
Para evitar que se pierda información relevante de la anatomía del rostro, se deben considerar los puntos donde se encuentran singularidades en la curvatura, es decir, los umbilics. Estos se incluyen en la malla poligonal y se crean caras con los vértices del polígono más cercanos (figura 9), obteniendo la malla final (figura 10).
2. Resultados
Con el fin de determinar el comportamiento de la metodología de remallado en el rostro humano propuesta, se calculó el remallado en modelos neutros y modelos con expresiones, para lo cual se utilizó la base de datos BU–3DFE [15] . Esta base de datos de rostros en 3D incluye 2500 modelos de 100 sujetos (56 % femeninos, 44 % masculinos). Para cada sujeto se tienen 7 expresiones faciales: expresión neutra (figura 11(a)), felicidad (figura 11(b)), sorpresa (figura 11(c)), miedo (figura 11(d)), tristeza (figura 11(e)), disgusto (figura 11(f)) y enojo (figura 11(g)). Adicionalmente, cuenta con cuatro diferentes niveles de intensidad de cada expresión, de los cuales se utilizó el nivel máximo, donde la expresión está más definida.
2.1. Remallado de modelos en expresión neutra
Se aplicó el algoritmo a los 80 modelos de la base de datos en expresión neutra; en promedio se logró generar una malla con el 46 % de los vértices y con el 48 % de las caras de la malla inicial. En la figura 14(a)se muestra un modelo (malla inicial) que cuenta con 7740 vértices y 15 030 caras, y el remallado final (figura 12(b)) que requiere solo 3676 vértices y 7567 caras, es decir, un 47 % de los vértices y 50% de las caras. En las figuras, de izquierda a derecha, se presenta la nube de puntos, la malla, la malla con textura gris y, finalmente, la malla suavizada.
En el modelo masculino de la figura 13(a), la malla inicial cuenta con 9930 vértices y 18 241 caras; después del proceso de remallado fueron necesarios 5042 vértices y 10 160 caras (figura 13(b)), es decir, un 51 % de los vértices y un 56 % de las caras.
2.2. Remallado de modelos con expresiones faciales
Se calculó el remallado para 80 rostros: 40 mujeres y 40 hombres. En promedio se logró generar una malla con el 46 % de los vértices y con 47 % de las caras, de la malla inicial. La desviación estándar del número de vértices y caras fue del 4.2 y 4.8, respectivamente. En la figura 14 se muestra el resultado del remallado (R) comparado con la malla inicial (MI), para cada una de las expresiones faciales.
2.3. Validación de la calidad del remallado
La definición de la calidad del remallado no se puede unificar o estandarizar para todas las técnicas; por esto para el remallado poligonal anisotrópico, no son relevantes criterios como distribución de los vértices, puesto que no se busca generar mallas con elementos similares; de hecho, se busca reducir el número de caras utilizando polígonos en cambio de triángulos (para la generación de un cuadrilátero se requieren 2 triángulos, es decir 2 caras por polígono). Tampoco tiene relevancia el criterio de la cantidad de elementos, puesto que el hecho de que la malla resultante tenga menos elementos no implica que tenga mejor calidad, porque solo con la cantidad de caras no se asegura la fidelidad anatómica.
Con el fin de estudiar la relación que existe entre los puntos característicos de la antropometría facial y los puntos clave del remallado, se realizó un experimento donde se calcularon las distancias de los 60 puntos anatómicos con los que cuenta la base de datos, y los vértices de las mallas iniciales, para analizar qué tanto se ajusta la malla generada por las líneas de curvatura a estos puntos de relevancia anatómica. Se comprobó que en los puntos con relevancia anatómica, los puntos generadores del remallado se ajustan mejor que los vértices de la malla inicial, con lo que se obtuvo una mejora promedio en la calidad del ajuste anatómico del 22 % para modelos neutros, y de 20 % para modelos con expresiones faciales. Otro criterio que se aplicó fue el error de aproximación medio (emedio) y máximo (emax) entre las mallas, obtenido las ecuaciones 2 y 3, respectivamente.
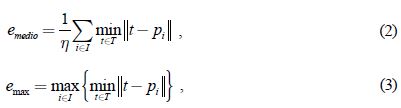
donde T representa el conjunto de puntos de la malla inicial, t el punto actual, I el conjunto de todos los puntos del remallado, pi el punto del remallado con el que se está comparando y η la cardinalidad del conjunto I.
Se calculó este error entre la malla inicial y el remallado, para modelos neutros emedio en promedio fue de 0.54 mm, y emax en promedio fue de 1.04 mm. En la figura 15(a)se muestra la malla en la que se obtuvo el mayor error emedio que coincide con la que tiene el máximo emax. En la figura 15(b)se muestra el modelo que obtuvo el menor emedio . Este mejor ajuste puede ser producto de la curvatura propia del modelo, es decir, que si los modelos presentan una distribución de curvatura suave, las líneas de curvatura describirán la forma acercándose a los vértices de la malla inicial; pero si la curvatura tiene una distribución altamente cambiante a lo largo del modelo, las líneas de curvatura estarán más lejos de los vértices iniciales, y el error de aproximación será mayor.
En la tabla 1, se muestra el error de aproximación medio promedio, para cada grupo de modelos con la misma expresión. Se evidencia que la expresión de miedo presenta un menor error; y que el error de aproximación al modelo inicial es similar sin importar la expresión facial del modelo.
2.4. Error basado en la distancia de Hausdorff
Las validaciones realizadas con base en la distancia euclídea establecen la distancia geométrica entre dos puntos. En el estudio de mallas, existe un método que aborda el problema de comparación de las mallas cuando la distancia punto a punto no aporta la suficiente información; por ejemplo, cuando una de las mallas tiene mucho menos puntos que la otra (caso del remallado poligonal anisotrópico). Este método, busca la comparación no solo de un punto, sino de grupos de puntos, mediante la medición del error basado en distancia de Hausdorff [16, 17] . Esta distancia se puede definir como la máxima distancia desde un conjunto de puntos, al punto más cercano de otro conjunto [18] . Si X = x1, x2, ... xm y Y = y1, y2, ..., yn son dos subconjuntos de puntos, la distancia Hausdorff se calcula como:
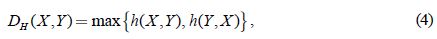
donde,
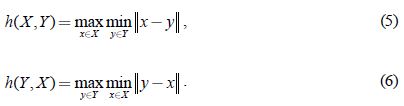
Considerando esta distancia como el error de aproximación, se calculó para todos los modelos y se obtuvo, en promedio, para modelos neutros un error de 1.04 mm, y para modelos con expresión de 1.11 mm. En la tabla 2 se muestra el error de aproximación promedio para cada grupo de modelos con la misma expresión. Se encontró el mínimo error en la expresión de miedo, confirmando el resultado del cálculo del error de aproximación.
2.5. Análisis visual de la calidad del remallado
Con el fin de mejorar la interpretación de los resultados, se presenta la métrica de Hausdorff de forma gráfica, comparando la malla inicial con el remallado (figura 16). Se representó la diferencia entre las mallas por medio del color; en rojo se muestran los puntos de máxima diferencia, y en azul, los puntos con mínima diferencia; a los valores intermedios se les asignó un degradé que pasa por naranja, amarillo y verde.
La figura 17 ilustra los resultados de comparación en las diferentes expresiones faciales. En cada caso se muestran la malla inicial, el remallado y la diferencia basada en la métrica de Hausdorff, respectivamente.
Para los modelos neutros, la máxima diferencia se muestra en la figura 18(a), y el modelo con la mínima diferencia se muestra en la figura 18(b); los sectores que presentan la mayor diferencia son los extremos de la malla.
Para los modelos con expresión, la máxima diferencia se muestra en la figura 19(a)y corresponde a la expresión de tristeza. En cuanto al modelo con la mínima diferencia, se ilustra en la figura 19(b) y corresponde a la expresión de sorpresa. En general, las zonas que presentan la mayor diferencia son los extremos de la malla; esto debido a que la zona cambia de acuerdo a la segmentación del rostro, realizada manualmente durante la adquisición de la base de datos. Dicha zona, en general, no es relevante, ya que no aporta información del rostro o de la expresión.
2.6. Comparación con el método de simplificación de Quadric Error Metrics (QEM)
Con la intención de validar los resultados finales del remallado, se comparó la técnica de remallado propuesta, con una técnica de simplificación de superficie muy utilizada en el área del modelamiento tridimensional conocida como surface simplification using Quadric Error Metrics (SQEM) [19] . Dicha técnica, a pesar de haberse propuesto en 1997, sigue siendo de actualidad, y se encuentra implementada en diferentes softwares de computación gráfica. Se utilizó esta técnica puesto que asegura una aproximación de alta calidad y conserva las principales características del modelo, incluso después de una significativa simplificación. Para realizar la comparación se calculó la simplificación en modelos seleccionados aleatoriamente, utilizando la técnica basada en SQEM y el remallado propuesto, con un porcentaje de reducción igual con las dos técnicas. En la tabla 3 se muestran los resultados de esta simplificación en número de caras y vértices.
La reducción, en el método de simplificación basado en QEM solo se puede garantizar en el número de caras, puesto que los vértices resultantes son dependientes de las caras formadas. En este punto se ve la primera diferencia entre los dos métodos, el número de vértices es menor para el método de remallado propuesto, debido a que se utilizan polígonos para la formación de las caras y, en consecuencia, se requieren menos vértices para la simplificación. En la figura 20 se muestran los resultados de la simplificación para diferentes modelos con expresiones faciales.
Al realizar la primera valoración cualitativa se aprecia que la técnica de SQEM entrega mallas más suaves y ajustadas al modelo original. Se calculó y visualizó la distancia de Hausdorff entre el modelo inicial y los modelos simplificados por las dos técnicas; en la figura 21 se muestran los resultados. Se evidencia que, aunque el ajuste general al modelo inicial es de mayor calidad utilizando la simplificación QEM, el remallado poligonal tiene ajustes más uniformes en las zonas de relevancia antropométrica (figura 22). Esto debido, probablemente, a que el remallado propuesto tiene como guía para su generación la curvatura propia del modelo, por lo que es razonable que sean suaves los cambios en estas zonas.
3. CONCLUSIONES
Se desarrolló una metodología de remallado, basada en la curvatura, orientada a modelos del rostro humano, con la que se logró reducir la malla inicial en más del 45 % (vértices y caras), conservando la información relevante para los modelos del rostro, y teniendo en cuenta la dinámica que los caracteriza cuando están sujetos a expresiones faciales. La técnica de remallado propuesta permite un mejor ajuste de los puntos generadores de la malla final a los puntos anatómicos de relevancia, independiente de la expresión facial. Se mostró que al realizar el remallado siguiendo la curvatura de la malla, no se pierden las características anatómicas a pesar de la reducción tanto en vértices como en caras.
La métrica de Hausdorff aportó más información de la similitud de formas que la que aporta una medida de distancia punto a punto; por esto se pudo evidenciar, gráficamente, que el remallado tiene un ajuste bueno en las áreas de relevancia antropométrica, sin importar la expresión facial del modelo. Al comparar la calidad del remallado con la técnica de simplificación basada en QEM, se evidenció que el método propuesto tiene una distribución uniforme de las caras resultantes con respecto a las características del rostro, a pesar de que el ajuste de la simplificación no fue mejor.
La técnica propuesta no permite modificar la densidad de las líneas de curvatura; siempre genera el máximo número de líneas posibles, lo que dificulta procesos donde se quiera cambiar la densidad de los puntos clave del remallado. Este problema se podría mitigar modificando la densidad de la cuadrícula creada para la última etapa del proceso, definiendo el número de cuadros en la malla para cambiar el número de caras y vértices de la malla final, pero sin garantizar el ajuste anatómico, puesto que la reducción de la cuadrícula no está orientada a mantener los puntos más relevantes anatómicos, sino a un submuestreo aleatorio de los puntos generadores de curvatura.
NOTAS:
* Este trabajo es resultado de una investigación terminada, financiada por la Universidad Nacional de Colombia.
REFERENCIAS
[1] P. Alliez et al., ''Recent advances in remeshing of surfaces'', en Shape analysis and structuring, L De Floriana and M. Spagnuolo, eds., pp. 53–82, Berlin: Springer–Verlag, 2008.
[2] M. Yirci and I. Ulusoy, ''Regular remeshing of 3D human face models'', presentado en 17th Signal Processing and Communications Applications Conference, Turkey, 2009.
[3] L. Qu and G. Meyer, ''Perceptually driven interactive geometry remeshing'', presentado en 2006 symposium on Interactive 3D graphics and games, USA, 2006.
[4] V. Kraevoy and A. Sheffer, ''Cross–parameterization and compatible remeshing of 3D models'', ACM Transactions on Graphics, vol. 23, n.° 3, pp. 861–869, 2004.
[5] M. Fujita et al., ''Multiresolution interpolation meshes'', presentado en 9th Pacific Conference on Computer Graphics and Applications, USA, 2001.
[6] S. Yamakawa and K. Shimada, ''Triangular/quadrilateral remeshing of an arbitrary polygonal surface via packing bubbles'', presentado en Geometric Modeling and Processing, China, 2004.
[7] M. Attene et al., ''Edge–sharpener: Recovering sharp features in triangulations of non–adaptively re–meshed surfaces'', presentado en Eurographics/ACM SIGGRAPH symposium on Geometry processing, Germany, 2003.
[8] M. Kaiser et al., ''Dense point–to–point correspondences between 3d faces using parametric remeshing for constructing 3d morphable models'', presentado en IEEE Workshop on Applications of Computer Vision (WACV'2011), USA, 2011.
[9] W. Zhu et al., ''Reversely anisotropic quad–dominant remeshing'', presentado en IEEE Shape Modeling International Conference, France, 2010.
[10] P. Alliez et al., ''Anisotropic polygonal remeshing'', ACM Transactions on Graphics, vol. 22, n.° 3, pp. 485–493, 2003.
[11] M. Marinov and L. Kobbelt, ''Direct anisotropic quad–dominant remeshing'', presentado en 12th Pacific Conference on Computer Graphics and Applications, Korea, 2004.
[12] N. Ray et al., ''Periodic global parameterization'', ACM Transactions on Graphics, vol. 25, n.° 4, pp.1460–1485, 2006.
[13] D. Cohen–Steiner and J. M. Morvan, ''Restricted delaunay triangulations and normal cycle'', presentado en 19th ACM symposium on Computational Geometry, USA, 2003.
[14] O. Sorkine et al., ''Bounded–distortion piecewise mesh parameterization'', presentado en IEEE conference on Visualization, USA, 2002.
[15] L. Yin, et al., ''A 3d facial expression database for facial behavior research'', presentado en 7th International Conference on Automatic Face and Gesture Recognition, UK, 2006.
[16] M. Corsini et al, ''Watermarked 3–D mesh quality assessment'', IEEE Transactions on Multimedia, vol. 9, n.° 2, pp. 247–256, 2007.
[17] B. Radunovic, ''Convergence in hausdorff metric preserves geometric shape'', Mat. Vesnik, vol. 48, pp. 25–28, 1996.
[18] D.P. Huttenlocher et al., ''Comparing images using the hausdorff distance'', IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 15, n.° 9, pp. 850–863, 1993.
[19] M. Garland and P.S. Heckbert, ''Surface simplification using quadric error metrics'', presentado en 24th annual conference on Computer graphics and interactive techniques, USA, 1997.