ARTÍCULOS

Análisis y simulación de un rectificador trifásico controlado Active Front End (AFE)

Analysis and simulation of a three–phase controlled Active Front End Rectifier (AFE)

Daniel Darío Campo Ossa^*; Hernando Vásquez Palacios^**; Jorge Eliécer Quintero Calvache^***

* Ingeniero electrónico, Universidad del Valle, magíster en Ingeniería con énfasis en Automática, investigador, docente catedrático de la Universidad del Valle. Calle 13 100–00, Edificio 353, Teléfonos 57 2 3212100 Santiago de Cali, Colombia. Contacto: daniel.d.campo@correounivalle.edu.co

** Ingeniero electricista, Universidad del Valle. Diplom Ingenieur der Elektrotechnik, Technische Universität Braunscheweig, Alemania. Docente titular de la Universidad del Valle. Calle 13 100–00, Edificio 353, Teléfonos 57 2 3391780. Telefax: 3392361–3392140. Santiago de Cali, Colombia. Contacto: hernando.vasquez@correounivalle.edu.co

*** Ingeniero electricista, Universidad del Valle. Magíster en Sistemas de Generación de Energía Eléctrica. Docente titular de la Universidad del Valle. Calle 13 100–00, Edificio 353, Teléfonos 57 2 3391780 Telefax: 3392361 – 3392140. Santiago de Cali, Colombia. Contacto: jorge.quintero@correounivalle.edu.co

Recibido: 14/03/2014
Aceptado: 26/02/2015

RESUMEN

Este artículo presenta un resultado de investigación financiado con recursos propios en el que se expone un modelo en espacio de estados de un rectificador trifásico controlado active front end. Utilizando este modelo se deriva una ley de control orientado al voltaje (VOC), enfocado en el comportamiento como carga resistiva, factor de potencia unitario, el cual es probado mediante simulación usando el Toolbox SimPowerSystem en Simulink de Matlab^®.

PALABRAS CLAVE: convertidor de potencia AC–DC, factor de potencia, modelo matemático, rectificador de frente activo controlado, rectificador trifásico.

ABSTRACT

This paper presents a result of research financed with own resources; It presents a state–space model of a three–phase controlled Active Front End rectifier. Using this model, we design a control law oriented voltage (VOC), directed to behavior as resistive load, unity power factor, which is tested by simulation using SimPowerSystem Toolbox in Matlab – Simulink ^®.

KEY WORDS: AC–DC power conversion, controlled active front end rectifier, power factor, mathematical model, three phase rectifier.

INTRODUCCIÓN

El desarrollo de nuevas topologías y de funcionalidades de los convertidores de potencia AC–DC van de la mano, como es natural, con la evolución de los dispositivos electrónicos de potencia. La estructura más clásica y extendida es el puente rectificador monofásico o trifásico en sus versiones con diodos o con tiristores. Estos convertidores se comportan como cargas no lineales, que generan corrientes armónicas en la red de suministro eléctrico [1]. La gran proliferación de estos convertidores, como fuente de alimentación de tensión continua de la mayoría de equipos electrónicos modernos de múltiples aplicaciones, en todos los rangos de potencia, hace necesaria la publicación de normativas reguladoras sobre las perturbaciones que se generan en la red de suministro eléctrico y en especial en el ámbito industrial, mediante el cumplimiento de la norma IEC 61000–3–2 y la norma IEEE 519–92 y en Colombia la resolución CREG–108 de 1997. Aunque difieren en naturaleza, fijan un máximo de distorsión armónica permitida [2, 3].

Para superar la problemática de las restricciones de armónicos de corriente en los sistemas de distribución de potencia, se han propuesto nuevas estructuras para la función de rectificación. Los rectificadores controlados de frente activo final por sus siglas en inglés (Active Front End, AFE) han sido investigados desde las últimas dos décadas y ofrecen una alternativa viable de reemplazo del tradicional y clásico rectificador controlado. Las principales características de la tecnología AFE son la baja generación de corriente armónica de baja frecuencia debido al control por modulación de ancho de pulso (PWM) [2–6], corrección del factor de potencia (PFC) [7, 8], con un factor de potencia cercano a la unidad, requerimientos de filtrado sustancialmente pequeños [9, 10], y una capacidad inherente de regeneración, con una gran variedad de esquemas de control [11–15].

En este trabajo se presenta un modelo en espacio de estados de un rectificador trifásico controlado active front end. Utilizando este modelo se deriva una ley de control orientado al voltaje (VOC) [11, 13], enfocado en el comportamiento como carga resistiva. Para ayudar en la mitigación de la problemática antes planteada, se presenta la descripción de la topología, el principio de operación básico del rectificador trifásico (AFE) para obtener su representación en espacio de estados; este modelo permite establecer una ley de control la cual es probada mediante simulación usando el Toolbox SimPowerSystem en Simulink de Matlab^®.

1. DESCRIPCIÓN DEL RECTIFICADOR TRIFÁSICO ACTIVE FRONT END (AFE)

La topología del rectificador trifásico de dos niveles (AFE) se muestra en la figura 1. Se trata de un conversor fuente de tensión (''Voltage Source Converter'' VSC) de dos niveles, el cual se puede comportar como rectificador (''Voltage Source Rectifier'' VSR) o como inversor (''Voltage Source Inverter'' VSI) en función del sentido que tenga el flujo de potencia. Por tanto, se trata de una estructura completamente bi–direccional (''back–to–back''). Cuando la transferencia de energía se presenta de la red eléctrica al bus de continua, reciben el nombre de rectificadores PWM (''Pulse Width Modulation''), rectificadores activos, rectificadores ''boost'', ''active front end'' [16].

Esta topología tiene numerosas ventajas frente a los rectificadores no controlados o controlados basados en diodos rectificadores o tiristores, respectivamente. Algunas de estas son: menor rizado del bus de DC, con condensadores menores, control del flujo de potencias activa y reactiva entre la red eléctrica y el convertidor, reducción de la distorsión armónica de la corriente de la red eléctrica, control del factor de potencia de desplazamiento (DPF), compensación de la potencia reactiva.

Lo anterior se logra al tener un rectificador activo que trabaja como etapa interfaz, entre la red de suministro eléctrico y la carga DC, principalmente para obtener una corriente AC en fase con un voltaje de red y una baja distorsión armónica de la corriente AC. Ello significa que en las formas de onda del voltaje y la corriente predominará el armónico fundamental, y los otros armónicos tendrán un valor cercano a cero. La condición de estar en fase el voltaje de la red con la corriente AC garantiza un comportamiento resistivo, es decir, potencia reactiva nula, independientemente que la carga DC sea lineal, no lineal, pasiva o activa.

2. PRINCIPIO DE OPERACIÓN

El principio de operación básico del rectificador trifásico AFE consiste en mantener el nivel del voltaje del bus de DC en un valor de referencia deseado; al usar un lazo de control realimentado para cumplir con esta tarea, el voltaje de DC es medido y comparado con la referencia Vref generando una señal de error la cual servirá como una nueva referencia al lazo de control interno encargado de modificar el comportamiento del encendido o apagado de los transistores IGBT; de acuerdo con la estrategia de control implementada se podrá disponer de la energía eléctrica de acuerdo a las necesidades de la carga final.

La figura 2 presenta el diagrama en una fase del rectificador Active Front End. En estado estable la ecuación 1 nos permite observar la operación del rectificador con factor de potencia unitario [17, 18].

3. MODELO MATEMÁTICO DEL RECTIFICADOR TRIFÁSICO ACTIVE FRONT END (AFE)

Para obtener el modelo del rectificador trifásico AFE, figuras 1 y 2, en ecuaciones de estado se hace en dos partes: sumatoria de voltajes de entrada y sumatoria de corrientes de salida.

La sumatoria de voltajes de entrada de cada fase representada de forma vectorial:

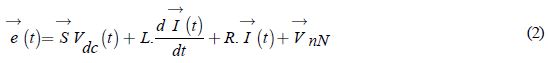
Sumatoria de corrientes de salida:

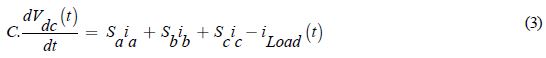
Donde:

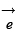= e_a,e_b, e_c : Son los voltajes de línea en la entrada del rectificador.

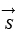= S_a, S_b, S_c : Son los estados de conmutación del puente rectificador

V_nN : Voltaje de desbalance del neutro.

R : Es la resistencia de la inductancia de entrada

L : Es la inductancia de entrada del rectificador

C : Es la capacitancia del bus de DC del rectificador

i_a, i_b, i_c : Son las corrientes de entrada al rectificador.

i_load : Es la corriente de la carga del lado de DC, (x₃/R_L).

Se asume que los dispositivos electrónicos de potencia son elementos de conmutación ideales y que no se tienen en cuenta las resistencias de los condensadores. Se asume que el sistema es balanceado; por lo tanto, el desplazamiento del neutro es igual a cero (V_nN=0).

Como se puede observar, las ecuaciones 2 y 3 dependen de los estados de conmutación del puente rectificador 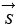= S_a, S_b, S_c, de valores [0, 1] los cuales dependen de la modulación que se realice. Si se asume que la frecuencia de conmutación de los IGBT se hace a una frecuencia superior a 100 veces frecuencia de la red, se puede aproximar 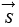a un ciclo de trabajo variable con el tiempo; para efectos de este modelo se toma una modulación senoidal.

Haciendo uso de la transformación al sistema complejo mediante 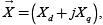para descomponer la ecuación 2 en el sistema de coordenadas (dq0), que permite representar las variables senoidales del sistema de coordenadas trifásico por valores constantes, se consigue trabajar con señales de control de naturaleza no oscilatoria. Después de un despeje matemático se obtiene el sistema de ecuaciones en espacio de estados donde: x₁=i_d, x₂=i_q y x₃=V_dc.

Modelo del rectificador trifásico no lineal:

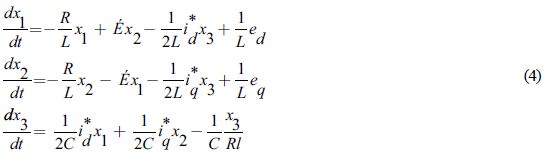
4. ANÁLISIS DE ESTABILIDAD DEL SISTEMA EN EL PUNTO DE EQUILIBRIO

Para el análisis del punto de equilibrio se deben determinar los siguientes parámetros del sistema:

• Voltaje de alimentación (Vrms línea – línea)

• Frecuencia de la red.

• Inductancia de entrada del rectificador.

• Condensador del bus de DC.

• Corriente de la carga.

• Resistencia de línea. (Despreciable)

Conociendo estos valores se procede a reemplazarlos en el modelo no lineal representado por el sistema de ecuaciones 4, teniendo en cuenta que cuando se realiza el cambio de coordenadas a dq0 y se alinea el fasor de tensión con el eje ''d'', los valores de las componentes obtenidas, tienen la siguiente naturaleza:

Como se puede ver en la ecuación 5, el valor de e_d corresponde al voltaje RMS línea–línea de la señal del voltaje trifásico en las fases abc, mientras que las otras dos componentes son cero cuando el voltaje de original no posee desfases adicionales entre líneas. De esta manera toda señal trifásica transformada en coordenadas dq0 con esta característica tendrá solo un valor en la componente ''d'' mientras que las otras dos componentes son cero.

Por otra parte, para lograr un comportamiento como carga resistiva, en el punto de operación deseado, la corriente de entrada no debe estar desfasada con respecto al voltaje de fase de entrada trifásico, por lo cual se entiende que el consumo del rectificador es de potencia activa (factor de potencia unitario); por lo tanto, el valor de la corriente en coordenadas dq0 debe tener una componente ''q'' igual a cero.

Para estas condiciones se calcula el punto de equilibrio del rectificador trifásico Active Front End de los estados x₁, x₂, x₃. Conociendo estos valores se procede a verificar la estabilidad del punto de equilibrio; para esto se calcula la matriz Jacobiana del modelo descrito por el sistema de ecuaciones 4, se evalúa en el punto de equilibrio y se determinan los valores propios del mismo. Al resolver el sistema de ecuaciones los valores propios son negativos, entonces el punto de operación es estable.

5. DISEÑO DEL CONTROL ORIENTADO AL VOLTAJE PARA EL SISTEMA LINEALIZADO DEL RECTIFICADOR ACTIVE FRONT END

Para el diseño del control orientado al voltaje, figura 3, se utiliza el sistema de ecuaciones 4 del modelo del rectificador trifásico no lineal y los valores del punto de equilibrio.

Al reorganizar se obtiene la representación en espacio de estados del sistema lineal:

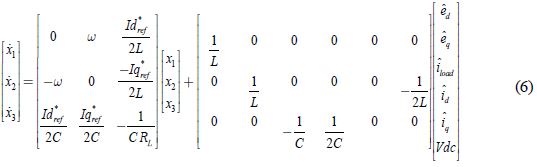
Donde:

Estados

x₁ Componente ''d'' de la corriente senoidal trifásica de entrada del rectificador

x₂ Componente ''q'' de la corriente senoidal trifásica de entrada del rectificador

x₃ Voltaje de salida del rectificador

Entradas

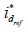Componente ''d'' de la señal senoidal trifásica moduladora de control

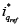Componente ''q'' de la señal senoidal trifásica moduladora de control

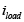Corriente a través de la carga (Disturbio)

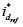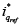Las variables a controlar para el rectificador son: el voltaje de salida Vdc = x₃, y la corriente I_q = x_2, la cual debe permanecer en todo momento en cero para garantizar un factor de potencia unitario. Se tienen dos entradas de control y para controlar dos variables de salida obteniéndose un sistema MIMO de 2x2, ecuación 7, para el cual se decide aplicar una estrategia de control orientado al voltaje.

Para iniciar con el diseño del sistema de control, es necesario analizar qué tan relacionadas están las entradas con las salidas; para ello se realiza un análisis de ganancia relativa en el sistema [19], Una vez se haya calculado la matriz de ganancias relativas, se lleva a cabo el análisis para seleccionar los pares entrada salida más conveniente para controlar. (ver tabla 1).

Se calcula la matriz de funciones de transferencia del sistema G, con la ayuda de los comandos de Matlab ''sys = ss(A,B,C,D)'', ''[num,den] = tfdata(sys)'', ''G= tf(num,den)'' utilizando el sistema en espacio de estados ecuación 6.

Matriz de funciones de transferencias:

Calculando RGA, la matriz de ganancias relativas del sistema de la ecuación 6, a través de la ecuación 7 se obtiene la tabla 1.

Como se puede ver las combinaciones 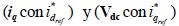tienen ganancias relativas negativas lo cual no es deseable por ser relaciones que indican inestabilidad; por otro lado, se puede ver que las combinaciones 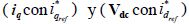tienen ganancias positivas y mayores a uno; aunque indican que el efecto de los otros lazos se inhibe por la acción de control, es la única opción viable para controlar este sistema. Por lo tanto se procede a hacer una ley de control de tal manera que el voltaje de DC sea controlado usando la variable manipulada 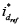y la corriente i_q sea controlada usando la variable manipulada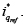

Se obtienen las dos funciones de transferencia del sistema independientes que permiten controlar el voltaje del bus de DC y la corriente i_q quedando definidas para el caso de estudio en particular de la siguiente manera:

6. RESULTADOS

6.1 Control de corriente i_q

Haciendo uso de la herramienta de Matlab Sisotool, se ajusta un controlador PI para la función de transferencia G_12, Ecuación 8. Se escoge un controlador tipo PI por que para este caso se necesita que la corriente i_q sea cero para poder asegurar que no exista un desfase entre la corriente de línea y el voltaje de fase de entrada del rectificador. Por otra parte, se necesita que esta regulación se haga lo más rápido posible, así que se ajusta el controlador de tal forma que se consiga el tiempo de estabilización más pequeño que permita el sistema utilizando la herramienta Sisotool de Matlab se consigue calcular y ajustar un controlador PI. En la figura 4, se observa la respuesta en lazo cerrado y la respuesta en frecuencia.

La respuesta temporal del sistema con el controlador se presenta en la figura 5; en esta se observa que la respuesta al escalón unitario tiene un sobrepaso del 31.4%, con un tiempo de estabilización de aproximadamente 32 ms.

6.2 Control interno de corriente ID

Si se asume que el control de i_q asegura siempre un aporte nulo de esta corriente, el sistema a controlar quedaría desacoplado. Se puede observar que para controlar el voltaje del bus de DC, se necesita tener control de la dinámica correspondiente a la corriente i_d, en concordancia con la topología del control VOC [11], además de diseñar un control en cascada, con un controlador interno para la corriente i_d, y un controlador externo para el voltaje V_dc. Para el controlador interno es necesario conocer la función de transferencia que relaciona i_d con i*_dref. Haciendo uso de la herramienta de Matlab Sisotool se ajusta un controlador PI para la función de transferencia G_21, ecuación 9.

Se escoge un controlador tipo PI para la corriente i_dsiga la i*_dref lo más rápido posible y se ajusta el controlador de tal forma que se consiga el tiempo de estabilización más pequeño que permita el sistema. Utilizando la herramienta Sisotool de Matlab se consigue calcular y ajustar un controlador PI; en la figura 6, se observa la respuesta temporal del sistema controlado en lazo cerrado para la corriente i_d.

6.3 Control lazo externo de voltaje Vdc

Con el control interno de corriente, se procede a encontrar la función de transferencia del sistema en lazo cerrado, pero esta función de transferencia no se puede obtener directamente de las matrices de estado como se ha hecho hasta el momento, pero sí se puede utilizar la relación 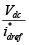y 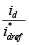para despejar la relación 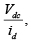y multiplicarla con la función de transferencia del controlador de corriente i_d 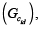con lo que se obtiene:

Con función de transferencia de la ecuación 10 se calcula un controlador PI. La respuesta temporal del sistema controlado en lazo cerrado para el voltaje Vdc se puede ver en la figura 7.

CONCLUSIONES

En este estudio se alcanzó el objetivo de diseñar y simular un rectificador trifásico controlado Active Front End de baja potencia, a través de una serie de pasos que comienzan desde el modelado matemático del rectificador, para continuar con el diseño del sistema de control, verificando mediante simulaciones el comportamiento de todo el sistema.

El diseño de la ley de control orientado al voltaje VOC para el sistema no–lineal de un rectificador trifásico controlado Active Front End brinda los resultados esperados en los rangos cercanos al punto de operación mediante un control lineal basado en el sistema linealizado del rectificador, comprobando que las respuestas del sistema son más rápidas frente a perturbaciones.

REFERENCIAS

[1] F. Martínez, ''Técnicas de Conversión AC/DC en Sistemas Monofásicos con Factor de Potencia Unitario'', Tecnura , vol. 6, n.° 12, pp. 31–41, 2003.

[2] A. Prudenzi, U. Grasselli, R. Lamedica, ''IEC Std. 61000–3–2 harmonic current emission limits in practical systems: need of considering loading level and attenuation effects'', Power Engineering Society Summer Meeting, 2001, vol.1, pp. 277–282.

[3] ''IEEE Recommended Practices and Requirements for Harmonic Control in Electrical Power Systems'', IEEE Std 519–1992, 1993.

[4] T. Noguchi, H. Tomiki, S. Kondo,I. Takahashi, ''Direct power control of PWM converter without power–source voltage sensors'', IEEE Trans. Ind. Applicat, vol. 34, pp. 473–479, May/June 1998.

[5] J. R. Espinoza, G. Joos, E. Araya, L. A. Moran T, D. Sbarbaro, ''''Decoupled control of PWM active–front rectifiers using only DC bus sensing'', Industry Applications Conference, 2000. Conference Record of the 2000 IEEE, vol. 4, pp.2169–2176, Oct 2000.

[6] J.W. Kolar, T. Friedli, ''The essence of three–phase PFC rectifier systems'', Telecommunications Energy Conference (INTELEC), 2011 IEEE 33rd International, vol., no., pp.1–27, 9–13 Oct. 2011.

[7] J. Muhlethaler, M. Schweizer, R. Blattmann, J. W. Kolar, A. Ecklebe, ''Optimal design of LCL harmonic filters for three–phase PFC rectifiers'', IECON 2011 – 37th Annual Conference on IEEE Industrial Electronics Society , vol., pp. 1503–1510, 7–10 Nov. 2011.

[8] K. Nishimura, K. Atsuumi, K. Tachibana, K. Hirachi, S. Moisseev, and M. Nakaoka, ''Practical performance evaluations on an improved circuit topology of active three–phase PFC power converter'', in Proc. IEEE APEC''01, 2001, pp. 1308–1314.

[9] M. Liserre, F. Blaabjerg, S. Hansen, ''Design and control of an LCL–filter–based three–phase active rectifier'', Industry Applications, IEEE Transactions on, vol. 41, n.° 5, pp. 1281–1291, Sept.–Oct. 2005.

[10] M. Liserre, F. Blaabjerg, R. Teodorescu, ''Grid impedance detection via excitation of LCL–filter resonance'', Industry Applications Conference, 2005. Fourtieth IAS Annual Meeting. Conference Record of the 2005, vol. 2, pp. 910– 916.

11] M. Malinowski, M. P. Kazmierkowski, A. M. Trzynadlowski, ''A comparative study of control techniques for PWM rectifiers in AC adjustable speed drives'', Power Electronics, IEEE Transactions on , vol. 18, n.° 6, pp. 1390–1396, Nov. 2003.

[12] M. Malinowski, M. P. Kazmierkowski, S. Hansen, F. Blaabjerg, G. D. Marques, ''Virtual–flux–based direct power control of three–phase PWM rectifiers'', Industry Applications, IEEE Transactions on , vol. 37, n.° 4, pp. 1019–1027, Jul/Aug 2001.

[13] M. P. Kazmierkowski, L. Malesani, ''Current control techniques for three–phase voltage–source PWM converters: a survey'', Industrial Electronics, IEEE Transactions on, vol. 45, n.° 5, pp. 691–703, Oct 1998.

[14] J. W. Dixon, J.M Contardo, L. A. Moran, ''A fuzzy–controlled active front–end rectifier with current harmonic filtering characteristics and minimum sensing variables'', Power Electronics, IEEE Transactions on , vol.14, n.° 4, pp. 724–729, Jul 1999.

[15] S. Hansen, M. Malinowski, F. Blaabjerg, M. P. Kazmierkowski, ''Sensorless control strategies for PWM rectifier'', Applied Power Electronics Conference and Exposition, 2000. APEC 2000. Fifteenth Annual IEEE, vol. 2, pp. 832–838.

[16] M. P. Ka?mierkowski, R. Krishnan, F. Blaabjerg, Control in power electronics: selected problems, USA: Academic Press Series in Engineering, 2002.

[17] J. W. Dixon, ''Three–Phase Controlled Rectifiers'', Chapter 12 in ''Power Electronics Handbook'', Academic Press, London, August 2001, pp. 183–196.

[18] A.Ya. Mikitchenko, P.R. Shestakov, V.G. Bessonov, A.N. Shevchenko, ''Research of active–front end modes in direct and alternating transistor electric drive'', 2010, published in Elektrotekhnika, N.° 7, pp. 52–57, 2010.

[19] S. Skogestad, I. Postlethwaite, Multivariable Fedback Control. Analysis and Design. Second Edition, Wiley, Pp. 82–90, 2007.