ARTÍCULO ORIGINAL

ESTUDIO DEL MODELAMIENTO DE LA CALIDAD DEL AGUA DEL RÍO SINÚ, COLOMBIA

STUDY OF THE WATER QUALITY MODELING OF THE SINÚ RIVER, COLOMBIA

Diana Marcela Arroyave Gómez^*; Agustín Alejandro Moreno Tovar^**; Francisco Mauricio Toro Botero^***; Darío de Jesús Gallego Suárez^****; Luis Fernando Carvajal Serna^*****

^* M. Sc. Materiales y Procesos, Universidad Nacional de Colombia-Sede Medellín, e-mail: dmarroya@unal.edu.co

^** M. Sc. Recursos Hidráulicos, Universidad Nacional de Colombia Sede Medellín, e-mail: aamoreno@unal.edu.co

^*** Ph. D., Profesor Titular Facultad de Minas, Universidad Nacional de Colombia, Sede Medellín, e-mail: fmtoro@unal.edu.co

^**** M. Sc., Profesor Asociado, Escuela de Procesos y Energía, Universidad Nacional de Colombia, Sede Medellín, e-mail: dgallego@unal.edu.co

^***** M. Sc., Profesor Asociado, Facultad de Minas, Universidad Nacional de Colombia, sede Medellín, e-mail: lfcarvaj@unal.edu.co

Recibido: 31/10/2012

Aceptado: 07/05/2013

RESUMEN

En este estudio se presenta la modelación de la calidad del agua en el río Sinú, Colombia, en el tramo central entre la central hidroeléctrica de Urrá y la desembocadura al mar Caribe, usando el modelo QUAL2KW que incorpora el algoritmo genético PIKAIA, que permite la calibración de las constantes cinéticas. Específicamente, se presenta la metodología usada para la caracterización hidráulica, la segmentación de la corriente y el uso del método de muestreo Monte-Carlo para determinar los parámetros de calidad de agua de mayor sensibilidad, y demostrar que el modelo QUAL2KW no pudo ser calibrado para el río Sinú con la información de campo disponible, debido a que varias combinaciones de los parámetros producen soluciones igualmente óptimas.

PALABRAS CLAVE

Algoritmo genético, QUAL2KW, Monte Carlo, modelamiento de la calidad del agua.

ABSTRACT

In this work a water quality modeling study of the Sinú river, Colombia, is presented in the segment from Urrá hydroelectric generation power plant to Caribbean sea mouth using the QUAL2KW model which incorporates the PIKAIA genetic algorithm that allows the calibration of the kinetic constants for its application to any waterbody. Specifically, the study shows the methodology used for the hydraulic characterization, the segmentation of the stream and the use of the Monte Carlo sampling method to determine the most sensitive water quality parameters and to demonstrate that the QUAL2KW model could not be calibrated for the Sinú river with the available filed information, because several combinations of the parameters produced equally optimal solutions.

KEY WORDS

Genetic algorithm, QUAL2KW, Monte Carlo method, water quality modeling.

INTRODUCCIÓN

El desarrollo de políticas públicas para la gestión del recurso hídrico requiere establecer criterios de calidad de agua que deben alcanzarse para garantizar la sostenibilidad del recurso [1]. En este sentido, los modelos matemáticos de calidad de agua son herramientas que permiten entender y cuantificar las relaciones causa-efecto de los procesos físicos, químicos y biológicos en los cuerpos receptores. En la actualidad, estos modelos han sido utilizados para evaluar distintas alternativas de gestión para mejorar la calidad del agua siguiendo el enfoque clásico [2], el cual, una vez el modelo sea calibrado y validado, se utiliza para predecir la concentración de los contaminantes para distintas alternativas de tratamiento o de políticas de gestión del recurso hídrico [2, 3]. Adicionalmente, dentro del proceso de calibración de un modelo se debe considerar el comportamiento de los diferentes parámetros que simulan los procesos incluidos en él y, por lo tanto, se hace necesaria la implementación de una metodología que garantice una calibración apropiada de dichos parámetros, la cual permite al usuario el estudio detallado de escenarios definidos para la caracterización ambiental de la corriente.

En este artículo se presenta la metodología utilizada en la implementación del modelo de calidad del agua QUAL2KW en el río Sinú, Colombia, empleando la herramienta de los algoritmos genéticos (AG) disponible en el modelo para la calibración automática de los parámetros cinéticos. La metodología propuesta emplea información histórica de la calidad del agua en la corriente y los resultados de un modelo hidráulico unidimensional en estado permanente (modelo HEC RAS) para estructurar el modelo de calidad sobre la corriente. Adicionalmente, mediante el análisis de Monte Carlo se estudió la posibilidad de calibración del modelo con base en la información de campo disponible y se determinaron los parámetros de mayor sensibilidad.

1 MODELO QUAL2KW

1.1 Generalidades

El modelo QUAL2KW ha sido ampliamente utilizado para el modelamiento de la calidad de agua por varios autores (por ejemplo, Kannel et. al. [4] y Heon Cho y Ryong Ha [5]). Como caso especial, se menciona a Pelletier et al. [6] quienes desarrollaron su modelo modificando la versión original (QUAL2K) incluyendo el AG PIKAIA para la calibración de los parámetros cinéticos de la corriente [7, 8].

El modelo unidimensional QUAL2KW simula el impacto de cargas contaminantes puntuales y distribuidas en un flujo permanente, no uniforme, segmentando el sistema en tramos que pueden ser de longitud variable. El balance hidrológico se representa a través del flujo; el balance de calor, a través de la temperatura, y el balance de material, a través de la concentración de especies constituyentes. Los procesos cinéticos que se incluyen en el modelo son disolución, hidrólisis, oxidación, nitrificación, desnitrificación, muerte y respiración/excreción y fotosíntesis. Los procesos de transferencia de masa incluidos son re-aireación, sedimentación, demanda béntica de oxígeno y flujo de carbono orgánico de los sedimentos [4, 6, 8]. Considerando estos procesos, el modelo QUAL2KW simula el transporte de la temperatura, la demanda bioquímica de oxígeno carbonácea (DBOC), el fitoplancton, el oxígeno disuelto (OD), el material orgánico partículado, las diferentes formas de nitrógeno y fósforo, el pH, la alcalinidad, los sólidos suspendidos inorgánicos (SSI), los patógenos, las algas en el fondo de la columna de agua y en la zona hiporréica (estas dos últimas son simuladas para ríos poco profundos) [4, 6, 8]. La DBOC se representa de dos formas: la DBOC rápida que es la materia orgánica fácilmente oxidada por los microorganismos y la DBOC lenta que es la materia orgánica difícilmente biodegradable por la población bacteriana [6, 8].

1.2 Esquema numérico y coeficiente de dispersión longitudinal

El modelo QUAL2KW utiliza un esquema en diferencias finitas hacia atrás para solucionar las ecuaciones diferenciales, esquema que produce una sobrestimación del coeficiente de dispersión en la ecuación de transporte el cual debe ser corregido con un coeficiente de dispersión numérico [2]. El algoritmo de corrección, en primer lugar, determina el coeficiente de dispersión física longitudinal por medio de la relación de Fischer [6]:

Donde:

U_i es la velocidad media en el tramo i

B_i y H_i son el ancho y profundidad promedio del tramo, respectivamente

U^*_i la velocidad de corte.

Después de calcular la dispersión física, E_pi, el algoritmo determina la dispersión numérica como:

Donde:

Δx_i es la longitud del tramo i

E_n,i es la dispersión numérica (m²/s).

El coeficiente de dispersión utilizado por el modelo es E_i = E_pi – E_n,i, si el coeficiente E_p,i es mayor que el coeficiente E_n,i. Si esta condición no se cumple el modelo usa para los cálculos la dispersión numérica.

1.3 Algoritmo genético implementado en el modelo QUAL2KW

De forma general, un algoritmo genético (AG) es un sistema de búsqueda a través de un espacio de decisión, usando un proceso análogo al de la ''selección natural de las especies'' de Darwin, que busca la supervivencia, en mayor número, de los individuos más aptos. El sistema de optimización se basa en la aplicación de una serie de operadores genéticos (selección, cruce, mutación y plan de reproducción), que modelan el mecanismo de búsqueda [8-10]. Dado que los AG emplean la representación y los operadores de variación independientes de cada problema, se consideran como métodos robustos que pueden aplicarse a gran variedad de casos sin tener que adaptarse a cada problema particular [11]. El modelo QUAL2KW realiza la calibración automática de los parámetros cinéticos mediante el AG-PIKAIA, determinando sus valores óptimos entre máximos y mínimos especificados para cada parámetro, buscando maximizar la bondad de ajuste con respecto a los datos de campo [9].

2 MATERIALES Y MÉTODOS

2.1 Descripción del área de estudio

La cuenca del río Sinú está ubicada en la región nordeste de Colombia, entre los 8 ° y 9 ° de latitud norte y 75 ° y 76 ° de longitud oeste, cubriendo un área de unos 14.000 km² con una longitud total del cauce de 438 km hasta su desembocadura en el mar Caribe (ver figura 1). En su parte alta la corriente está controlada en su totalidad por el embalse multipropósito Urrá I (cuya cuenca tributaria es de unos 4.600 km²) con un caudal medio en el sitio de presa de 349 m³/s y una capacidad instalada de 340 MW. El tramo seleccionado para este estudio está comprendido entre el sitio de presa y la desembocadura del río en el mar Caribe (264 km de longitud), tramo que posee, en condiciones de banca llena, anchos promedio entre los 120 y 160 m y profundidades entre los 5 y 8 m. En la cuenca del río Sinú se encuentra asentado el 76 % de la población del departamento de Córdoba y en su recorrido suministra agua a los principales centros poblados de la cuenca, así como a vastas zonas de riego en su porción media-baja, en donde se cultivan especialmente arroz y algodón.

2.2 Información disponible

Para este estudio se dispone de información de campañas de medición de diversos parámetros de calidad del agua realizadas por la Corporación Autónoma Regional de los Valles del Sinú y del San Jorge (CVS), autoridad ambiental responsable del manejo del río Sinú, en 17 puntos a lo largo del trayecto en estudio entre los años 2002 y 2006. Se emplearon los datos de calidad del agua de la campaña de campo de 22 de enero de 2003, para la calibración, y la del 18 de diciembre de 2002, para la validación del modelo, dado que son las campañas más completas. Adicionalmente, se cuenta con un modelo hidráulico implementado en el tramo del río a estudiar (HEC RAS en su versión 3.1.3), el cual fue calibrado y validado para diversos escenarios hidrológicos [12].

2.3 Caracterización hidráulica

El modelo QUAL2KW determina la velocidad y la profundidad medias del flujo para cada tramo de la corriente usando uno de los siguientes tres métodos: la ecuación de flujo a través de vertederos de cresta delgada, curvas de potencia y la ecuación para flujo uniforme de Manning empleando una sección transversal regular de forma trapezoidal [2, 6]. La mejor opción de estas encontradas para el río Sinú fue la de las curvas de potencia [12, 13]:

Los coeficientes a, b, c,α, β, y f de las ecuaciones (3) a (5) se determinaron para cada sección del río mediante el ajuste de los valores de U, H y B provenientes de corridas del modelo hidráulico HEC RAS calibrado, para un rango de caudales entre valores máximos y mínimos medios diarios multianuales de la corriente. Detalles de la calibración y validación del Modelo HEC RAS se presentan en [12].

2.4 Segmentación de la corriente

Al realizar la segmentación de la corriente, deben considerarse tanto el coeficiente de dispersión como el criterio de estabilidad de la integración numérica, representado por la condición de Courant-Friderich-Lewis. En este caso, la segmentación del río se basó en un proceso de experimentación numérica, buscando segmentar la corriente de manera tal que se encuentre el máximo valor de la longitud de cada segmento para un tiempo de corrida dado que haga que el programa seleccione la dispersión física en lugar de la numérica, para el mayor porcentaje de tramos.

2.5 Valores de las variables meteorológicas

El balance de calor y temperatura es función de datos meteorológicos, tales como, temperatura del aire, temperatura del punto de rocío, humedad relativa, velocidad del viento y fracción del cielo cubierto por nubes. Esta información se obtuvo de la base de datos de la National Oceanic & Atmospheric Administration (NOAA) [13].

2.6 Valores de las variables de calidad

La DBOC de oxidación rápida se tomó como DBO₅ filtrada [3], la DBOC de oxidación lenta se tomó como la diferencia entre la DBO₂₀ total y la DBO₅ total. El material orgánico partículado, incluyendo los sólidos orgánicos suspendidos, (MOP) se calculó como la diferencia entre la DBO₅ total y la DBO₅ filtrada. En este trabajo se empleó la composición estequiométrica de la materia orgánica recomendada en el modelo, así: 100 gD: 40 gC: 7200mgN: 1000 mgP: 1000mgA, donde D, C, N, P y A se refieren a peso seco, carbono, nitrógeno, fósforo y clorofila, respectivamente. El valor de los sólidos suspendidos inorgánicos se determinó como la diferencia entre los sólidos suspendidos totales (SST) y los orgánicos. También se tuvieron como datos de entrada el pH, la temperatura, el OD, los nitratos y el amonio. Finalmente, el coeficiente de re-aireación se obtuvo mediante un proceso de experimentación numérica para caudales mínimos, medios y máximos (resultados no mostrados). De todas las opciones para calcular este coeficiente se seleccionó el método recomendado por el modelo, dado que su determinación depende de las características hidráulicas de la corriente reportadas en [6].

2.7 Selección de la función objetivo

Para la auto-calibración de los parámetros cinéticos por medio del AG se empleó la función recomendada por Kannel et. al [4] y Pelletier et al. [8]:

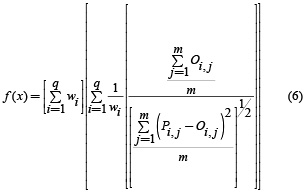
Donde:

O_i,j es el valor observado

P_i,j es el valor predicho por el modelo

m es el número de pares de valores observados y predichos

w_i es el factor de peso y q es el número de variables de estado.

En la práctica, los datos de calidad del agua son muchas veces distorsionados por ruido e incertidumbre a través del muestreo y análisis de laboratorio, obteniéndose una variabilidad de los grados de confiabilidad. Por consiguiente, es razonable asignar altos valores de peso a los datos más confiables, y menor valor a los datos menos confiables [14].

2.8 Análisis de sensibilidad e interacción de parámetros en el modelo

Un conocimiento previo de los efectos de los diferentes parámetros del modelo sobre la respuesta de calidad puede reforzar el proceso de calibración [2, 10]. Una vez configurado el modelo de calidad, y antes de iniciar su proceso de calibración, se realizó un análisis de los parámetros cinéticos con el fin de detectar parámetros interdependientes y/o la existencia de una posible equiafinidad de los mismos (distintas combinaciones de parámetros que producen soluciones igualmente óptimas) que no permitieran la calibración del modelo. Para este análisis, se empleó el método de muestreo Monte-Carlo en conjunto con la herramienta de análisis MCAT (Monte Carlo Analysis Toolbox) [15 - 17].

2.9 Calibración mediante algoritmos genéticos

Para la estimación de los parámetros de entrada del AG del modelo se usó el método de experimentación numérica aplicado a sus operadores más importantes: tamaño de la población inicial, número de generaciones y probabilidad de cruce. Los parámetros restantes fueron definidos con base en los valores y estrategias de optimización recomendados en la literatura [6, 8]. De esta manera, se seleccionó un modo de cruce híbrido que tiene igual probabilidad de cruce para los modos un punto, dos puntos y uniforme; el plan de reproducción empleado fue el de reemplazo total de la población en cada generación, junto con el modo de mutación ajustable y la estrategia de elitismo. Los valores de velocidad de mutación inicial, velocidad de mutación mínima y máxima, y el número de dígitos para codificar el genotipo correspondieron a los valores recomendados por defecto en el modelo [6].

2.10 Validación

Además de las estrategias de evaluación de los ajustes que se desarrollan en la etapa de calibración, se debe realizar un procedimiento de validación del modelo calibrado, con el fin de identificar posibles limitaciones y fortalezas cuando este se utilice en condiciones distintas a las del escenario de calibración.

3 RESULTADOS Y DISCUSIÓN

3.1 Caracterización hidráulica

En este estudio se encontró que de las curvas de potencia velocidad-profundidad y velocidad-ancho, las correlaciones en función del ancho se ajustan mejor al río Sinú. Este resultado se debe a que el modelo utiliza la relación presentada en la ecuación (1) para calcular la dispersión física, relación que se ve más afectada por el ancho que por la profundidad, característica del río Sinú. Al usar las correlaciones en función del ancho se observó que el porcentaje de tramos que utiliza el coeficiente de dispersión numérica es solo el 33 % del total, aproximadamente la tercera parte del valor correspondiente cuando se usa la relación en función de la profundidad.

3.2 Segmentación

Para una discretización espacial y temporal adecuadas, se probaron tamaños de malla de 500, 800, 1.200, 1.500, 2.000 y 3.000 m, y tamaños del intervalo de cálculo de 0.7, 1.4, 2.8 y 5.6 minutos. En la figura 2 se presenta el perfil de OD obtenido con diferentes tamaños de malla y se observa que al aumentar el tamaño del segmento de 800 m a 1.200 y 1.500 m no se presenta una diferencia apreciable en el perfil, la cual sí aumenta para las mallas de 2.000 m y 3.000 m. Este comportamiento se debe a que el porcentaje de tramos con dispersión numérica aumenta del 26 % para la malla de 800 m a 58 % para la de 3.000 m, por lo que hay una sobrestimación del coeficiente de dispersión que es más notoria en la parte final de la curva. Aunque la diferencia entre los perfiles de OD para las mallas de 800 m y 3.000 m es de tan solo del 5 % en la parte final de la curva, donde se presenta la mayor diferencia, se seleccionó la malla de 1500 m, porque los tiempos de cálculo son similares, y se obtuvo una mejor resolución espacial.

3.3 Análisis de sensibilidad e interacción de parámetros

Una vez definidas las discretizaciones espacial y temporal, se evaluó la equiafinidad de parámetros de calidad del modelo durante el proceso de calibración. Para esta tarea se realizaron 1300 simulaciones de Monte-Carlo en el tramo en estudio, en donde los valores de los parámetros cinéticos que se emplearon en cada simulación se seleccionaron a partir de una distribución uniforme en un intervalo físicamente probable, estimado según las condiciones generales del río Sinú. Los parámetros cinéticos a los que se les realizó este análisis fueron: la velocidad de sedimentación de los sólidos suspendidos inorgánicos (Vs), la velocidad de hidrólisis de la DBOC de oxidación lenta (hidroCL), la velocidad de oxidación de la DBOC de oxidación lenta (VOCL), la velocidad de oxidación de la DBOC de oxidación rápida (VOCR), la velocidad de nitrificación (Nitrif), la velocidad de hidrólisis del nitrógeno orgánico (HydroNO), y la velocidad de sedimentación de la materia orgánica partículada (VsMOP). En este análisis, cada parámetro se divide en 10 grupos, y a cada grupo se le calculó su función de distribución acumulada. Si el desempeño de un modelo es sensible a un parámetro, se observaría una gran diferencia entre las funciones de distribución acumuladas de los 10 grupos [17]. En la figura 3(a) se aprecia que el modelo no es sensible a Vs ni a VsMOP, para las 10 clases consideradas. En cambio, presenta una alta sensibilidad a la Nitrif y la HydroNO. El modelo es sensible, en menor escala, a las velocidades de hidrólisis y a la oxidación de la DBOC de oxidación lenta y rápida. Cada recuadro de la figura 3(b) representa una proyección de un parámetro cinético en una dimensión respecto a la función de ajuste considerada en la ecuación (6). Si un parámetro está bien identificado (cuando es factible su calibración), se observaría un mínimo en la superficie de cada recuadro; según esto, ninguno de los siete parámetros cinéticos está bien definido, lo que indica que el modelo no proporciona, en realidad, una verdadera caracterización del sistema modelado.

En la figura 4 se presenta el gráfico de contorno y la superficie de respuesta para Vs y hidroCL, en la cual se observan múltiples regiones igualmente óptimas frente al comportamiento de la función de ajuste (diversos puntos donde la función de ajuste es igualmente mínima), implicando una equiafinidad entre los parámetros. Los coeficientes cinéticos restantes presentaron el mismo comportamiento, corroborando los resultados de la figura 3(b).

Estos resultados indican que no es posible, con la información calidad de agua disponible, obtener una verdadera calibración del mismo para el río Sinú. Por lo tanto, se centraron los esfuerzos en configurar un modelo que proporcione resultados aceptables para las variables de mayor interés en el río (OD en nuestro caso), para lo cual se empleó el AG PIKAIA incluido en el QUAL2KW.

3.4 Calibración mediante algoritmos genéticos y validación

Para seleccionar el tamaño de la población, el número de generaciones y la probabilidad de cruzamiento se probaron los siguientes valores: a) para el tamaño de la población: 50, 200 y 500; b) para el número de generaciones: 40, 100, 200; y c) para las probabilidades de cruce: 0.25, 0.45, 0.5, 0.65 y 0.85. Como se aprecia en las figuras 5(a) y 5(b), no hay diferencia significativa en el ajuste al final de la evolución del AG para el número de poblaciones y generaciones analizadas y, por lo tanto, se seleccionó una población de 50 y un número de generación de 40, dado que con estos valores se alcanzó la convergencia a altos valores de ajuste con un menor tiempo de cálculo. En la figura 5(c) se presenta el ajuste de la función objetivo para diferentes valores de la probabilidad de cruce, y se escogió la probabilidad de cruce de 0.5 para la calibración del modelo, dado que con el mismo tiempo de cálculo, se alcanzó un ajuste comparativamente mayor, que con otro valor de probabilidad. Los valores de tamaño de la población, número de generaciones y probabilidad de cruce que se seleccionaron están de acuerdo con lo reportado en la literatura [15, 18]. Es importante anotar que el valor de estos operadores depende de las características del río y de la configuración del modelo que se use para la calibración.

En la función objetivo, ecuación (6), se probaron pesos iguales y pesos diferentes de las variables de calidad. Los valores de peso diferente se asignaron de la siguiente forma: el valor de peso más alto se le asignó al OD debido a que los datos de campo presentaban menor variabilidad que las demás variables de calidad. A los nitratos, a la VOCR y a la VOCL se les asignó un valor cuatro veces menor que el dado al OD, debido a que estos datos se tomaron directamente de los datos de campo y presentaban una variabilidad intermedia. A los sólidos suspendidos orgánicos e inorgánicos, nitrógeno orgánico y amonio se les asignó un valor de peso 20 veces menor que el dado al OD, debido a que se determinaron a partir de suposiciones y a que los datos de campo presentaron mayor variabilidad. En las figuras 6(a) y 6(b) se presentan los resultados del modelo para el OD comparado con los datos de campo, asumiendo pesos iguales y diferentes de las variables de calidad en la función objetivo. Se observó un efecto significativo en el valor de las constantes cinéticas en la parte final del perfil del OD al usar pesos iguales y diferentes de las variables, lo que era de esperarse, dado que hay variables que presentan mayor variabilidad que otras, desde la toma misma de las muestras. Los resultados del modelo para el OD usando pesos diferentes presentan un mejor ajuste a los datos de campo, según se observa de las figuras 6(a) y 6(b). Es de anotar que el valor de los parámetros cinéticos de la tabla 1, usando pesos diferentes en la ecuación (6), muestra una buena solución al sistema aunque no es la única, debido al problema encontrado de equiafinidad entre los parámetros.

En la figura 7 se presenta el perfil de OD obtenido en la etapa de validación del modelo con los valores de los parámetros cinéticos usando pesos diferentes de las variables de calidad. Este perfil presenta un comportamiento similar al obtenido en la calibración.

4. CONCLUSIONES Y RECOMENDACIONES

En este estudio se pudieron establecer condiciones iniciales del modelo QUAL2KW para el río Sinú: tamaño de la malla espacial, tamaño de intervalo de cálculo, las correlaciones que se ajustan mejor a las características hidráulicas del río y fijar los operadores para el AG.

El método de muestreo de Monte-Carlo en conjunto con el MCAT (Monte Carlo Analysis Toolbox) usado en este estudio mostró ser una herramienta poderosa que permitió el análisis de los parámetros cinéticos considerados y determinar que el modelo de calidad de aguas no podía ser calibrado con la información de campo disponible.

Aunque los valores de los parámetros cinéticos ofrecen una buena solución al sistema modelado, estos valores no son únicos; para mejorar la confiabilidad y la capacidad predictiva del modelo se debe introducir información adicional de las variables de calidad bajo diferentes condiciones hidrológicas.

Los resultados de OD del modelo presentaron un buen ajuste a los datos de campo, tanto en la etapa de calibración como en la de validación (figura 6 (b) y figura 7). Sin embargo, debe mejorarse la confiabilidad y la capacidad predictiva del modelo, debido al problema de equiafinidad encontrado entre los parámetros. Para lograr esta mejora, es necesario introducirle al modelo información adicional, especialmente de campañas de campo bajo diferentes condiciones hidrológicas, con información completa de variables de calidad, tales como, OD, DBO₅ filtrada y total, DQO, nitrógeno orgánico, amonio, nitratos, sólidos suspendidos totales (SST) y sólidos suspendidos inorgánicos (SSI). De igual manera, se recomienda determinar de forma experimental los coeficientes de dispersión, ya que los valores usados por el modelo son una estimación usando la relación de Fischer. En el caso de determinarse en campo los valores de los coeficientes de dispersión, debe tenerse en cuenta que la discretización espacial deberá ser dirigida a obtener una segmentación que garantice que los coeficientes de dispersión utilizados por el modelos sean los que representen el fenómeno físico, evitando utilizar aquellos representativos de la dispersión numérica.

5 AGRADECIMIENTOS

A la CVS y al PARH de la Universidad Nacional de Colombia sede Medellín.

REFERENCIAS

[1] Chihhao Fan, Chun-Han Ko, Wei-Shen Wang. An innovative modeling approach using QUAL2K and HEC-RAS integration to assess the impact of tidal effect on River Water quality simulation. Journal of Environmental Management. Vol. 90, 1824-1832, 2009.

[2] Chapra, S. Surface water-quality modeling. McGraw-Hill. New York. 844 pp. 1997.

[3] Cox B. A. A review of dissolved oxygen modelling techniques for lowland rivers. The Science of the Total Environment. Vol. 314 –316, 303–334, 2003.

[4] Kannel Pr, Lee S, Lee Ys Kanel Sr, Pelletier G. J. Application of automated QUAL2Kw for water quality modeling and management in the Bagmati River, Nepal. Ecol Model, Vol. 202, 503 -517, 2007

[5] Heon, Chou and Ryong, Ha. Parameter optimization of the QUAL2K model for a multiple-reach river using an influence coefficient algorithm. Science of the Total Environment, 408, 1985–1991. 2010

[6] Pelletier, G.j. Chapra, S. QUAL2Kw theory and documentation (version 5.1). A modeling framework for simulating river and stream water quality. Civil and Environmental Engineering Dept., Tufts University, Medford, MA. 104 pp. 2004. Disponible en Internet: http://www.ecy.wa.gov/programs/eap/models/. [Citado el 18 de marzo de 2006].

[7] Pelletier, G. J., Chapra, S. C. QUAL2K: A Modeling Framework for Simulating River and Stream Water Quality. Documentation and Users Manual. Civil and Environmental Engineering Dept., Tufts University, Medford, MA. 2003.

[8] Pelletier, G. J., Chapra, S., TAO, H. QUAL2Kw - A framework for modeling water quality in streams and rivers using a genetic algorithm for calibration. Environmental Modelling & Software. Vol. 21, 419-425, 2005.

[9] Reed, P., Minsker, B. y Goldber, D. Designing a competent simple genetic algorithm for search and optimization. Water Resources Research. Vol. 36, N.° 12, 3757-3761. 2000.

[10] Ng A.W.M., Perera B.J.C. Selection of genetic algorithm operators for river water quality model calibration. Engineering Applications of Artificial Intelligence. Vol. 16, 529–541, 2003.

[11] Sánchez, G. Diseño y evaluación de algoritmos evolutivos multiobjetivo en optimización y modelación difusa. [Tesis Ph. D], Universidad de Murcia. 356 pp. 2002.

[12] Unlamed-CVS. Simulación de la calidad del agua y reglamentación del río Sinú, departamento de Córdoba. Informe Final. Postgrado en Aprovechamiento de Recursos Hidráulicos, Universidad Nacional de Colombia Sede Medellín, 2007.

[13] NOAA Research. National Oceanic & Atmospheric Administration. Disponible en internet: http://www.cdc.noaa.gov/cdc/reanalysis/reanalysis.shtml. [Citado el 20 de octubre de 2006].

[14] Zou, R., Ling, W. S. Robust water quality model calibration using an alternating fitness genetic algorithm. ASCE Journal of Water Resources Planning and Management Vol. 130, N.° 6, 471-479. 2004.

[15] Wagerner, T., Wheather, H. y Lees M. Monte-Carlo Analysis Toolbox user manual, version 5. Penn State University, 46 pp. 2004

[16] Camacho, L. Calibración y comparación de modelos de transporte de solutos en ríos de montaña. En: XXII Congreso Latinoamericano de Hidráulica, ciudad de Guyana, Venezuela. 10 pp. 2006

[17] Céspedes, D. y Camacho, L. 2004. Metodología de calibración de modelos hidrológicos e hidráulicos de flujo no permanente-aplicación en la cuenca media del río Bogotá (Colombia). En: XXII Congreso Latinoamericano de Hidráulica, Sao Pedro, estado de Sao Pablo, Brasil.10 pp. 2004.

[18] Mulligan, A. E., Brown, L. C. Genetic algorithm for calibrating water quality models. ASCE Journal of Environmental Engineering. Vol. 124, N° 3, 202–211, 1998.