ARTÍCULO ORIGINAL

BÚSQUEDA ALEATORIA REPETITIVA BASADA EN CAOS^*

CHAOS-BASED REPETITIVE RANDOM SEARCH

^** Ingeniera de Sistemas e Informática, Universidad Nacional de Colombia, Medellín, Colombia (2010). Correo electrónico: agarciaga@unal.edu.co

^*** Ingeniera de Sistemas e Informática, Universidad Nacional de Colombia, Medellín, Colombia. Correo electrónico: amrestref@unal.edu.co

^**** Doctor en Ingeniería, Área de Sistemas Energéticos, Universidad Nacional de Colombia, Medellín, Colombia (2009); Magíster en Ingeniería de Sistemas, Universidad Nacional de Colombia, Medellín, Colombia (1997); Profesor Asociado de la Universidad Nacional de Colombia (sede Medellín, Colombia). Facultad de Minas. Medellín, Colombia. Correo electrónico: jdvelasq@unal.edu.co

Recibido: 09/02/2012

Aceptado: 07/05/2013

RESUMEN

En este artículo se presenta una modificación del algoritmo de búsqueda aleatoria repetitiva. En esta propuesta se propone cambiar los parámetros fijos, que son ingresados por el usuario, por valores deterministas usando un mapa caótico. El algoritmo propuesto se usó para optimizar 4 funciones de prueba bien conocidas en 10, 20 y 30 dimensiones. Para todas las funciones de prueba, el algoritmo propuesto converge a mejores puntos que los puntos óptimos obtenidos usando la versión tradicional en la que el usuario fija los parámetros. Los resultados obtenidos motivan a continuar con el desarrollo y pruebas del algoritmo propuesto, para un mayor conjunto de funciones de prueba y comparar con otros algoritmos heurísticos establecidos.

PALABRAS CLAVE

Algoritmos; caos; métodos de minimización; investigación de operaciones; métodos de optimización; métodos de búsqueda.

ABSTRACT

In this paper, we present a modification of the repetitive random search algorithm. In our proposal, we change the fixed parameters which values are set by the user, by deterministic values following a chaotic map. The proposed algorithm is used to optimize four well known test functions for 10, 20 and 30 dimensions. For all cases, our proposal converges to better points that the optimal points obtained using the traditional version with fixed values in the parameters. The obtained results encourage us to continue the development and testing of the proposal algorithm with a major suite of test functions, and to compare it with other well established heuristic algorithms.

KEY WORDS

Algorithms; chaos; minimization methods; operations research; optimization methods; search methods.

INTRODUCCIÓN

Muchos problemas en las ciencias aplicadas, como la ingeniería, la economía y las matemáticas, involucran el uso de técnicas de optimización global; aunque las técnicas basadas en gradientes han gozado de popularidad debido a su elegancia, su matemática y su rigurosidad, ellas pueden ser empleadas solamente en un número restringido de problemas; estas limitaciones están relacionadas con la disponibilidad de información sobre el gradiente de la función, la complejidad de la función objetivo y la dificultad del cálculo de sus derivadas, la falta de robustez ante la presencia de discontinuidades, la localidad de su ámbito de búsqueda y la presencia de múltiples óptimos locales [1].

El desarrollo de métodos heurísticos para la optimización de funciones no lineales no es un tema nuevo, y sus desarrollos prácticos se dan desde la década de los 60; entre los desarrollos preliminares se encuentran el método de Powell [2], la optimización aleatoria [3], la técnica de Hooke y Jeeves [4], el algoritmo de Nelder y Mead [5] y la búsqueda aleatoria repetitiva (RSS, por su sigla en ingles) [6]. No obstante, en las últimas décadas se ha dado un impresionante crecimiento en el desarrollo de nuevas metodologías; véanse [7-10] y las referencias en ellos. En muchas de las metodologías desarrolladas, el éxito en el proceso de optimización está condicionado a que el usuario fije valores apropiados para los parámetros que controlan el algoritmo de optimización; de este problema adolecen técnicas heurísticas como la RSS [6], y basadas en gradientes, tal como la regla delta generalizada, que es usada comúnmente para la optimización en modelos de redes neuronales artificiales [11].

La RRS es un método de búsqueda local y elitista, con un componente aleatorio, que no utiliza información del gradiente de la función; su estrategia es iniciar en un punto de arranque y luego crear un camino aleatorio, donde la dirección y el tamaño de paso son asignadas por una función que tiene en cuenta la dirección exitosa encontrada en la iteración anterior. Este algoritmo requiere de 2 parámetros fijos, que son especificados por el usuario, los cuales modifican de manera significativa el desempeño del algoritmo; esto representa un problema al momento de hacer uso de RRS, ya que deben ser fijados de acuerdo con la experticia del usuario, y ajustados a las características de cada problema particular.

Recientemente, la teoría de sistemas caóticos ha sido aprovechada para desarrollar nuevas metodologías de optimización [12-14]; una de sus aplicaciones más importantes es el uso de secuencias numéricas generadas a partir de un mapa caótico, en vez de generadores de números seudo-aleatorios [12, 13, 15, 16], así como también, la hibridación de algoritmos existentes [16-19].

El objetivo de este artículo es presentar un nuevo método híbrido que combina la RSS y la teoría de sistemas caóticos; específicamente, se plantea cambiar los parámetros de la RSS, que son fijados por el usuario, por valores deterministas generados usando un mapa caótico.

El artículo está organizado de la siguiente manera: en la siguiente sección se describe la generación de secuencias por medio de mapas caóticos (sección 2). Después, se describe la metodología propuesta para este estudio (sección 3). A continuación, se analiza el comportamiento del algoritmo propuesto, cuando se optimizan cuatro funciones de prueba (sección 4). Finalmente, se describen las conclusiones de este estudio (sección 5).

1. CAOS Y ALGORITMOS DE OPTIMIZACIÓN

El término caos se refiere, en el sentido matemático, a un comportamiento complejo, limitado, inestable e impredecible generado por un sistema simple no lineal y determinista, conocido como mapa caótico, de tal manera que las secuencias generadas son casi aleatorias y sensibles a las condiciones iniciales [20].

La teoría del caos ha sido usada en el desarrollo de técnicas novedosas para la optimización global, las cuales tienen tres direcciones de investigación: primero, la solución de problemas combinatorios, como el problema del viajero [21, 22]. Segundo, el desarrollo de los algoritmos de optimización de caos basados en la generación de secuencias caóticas en lugar de la generación de números aleatorios. Y tercero, la hibridización de algoritmos de optimización, incluyendo las técnicas basadas en gradientes [15, 17, 18], algoritmos genéticos [23, 24], métodos de punto interior [25], recocido simulado [26], la optimización de enjambre de partícula [27, 28], búsqueda tabú [29], búsqueda por coordenadas [30, 31] y algoritmos evolutivos [17], entre otros.

Uno de los mapas caóticos más conocidos corresponde a la parábola logística, definida como:

donde γ_n∈(0;1) y γ_n∉{0,25;0,5;0,75} ya que se generaría un comportamiento cíclico periódico. En la figura 1 se presenta una gráfica de una secuencia generada a partir de la ecuación (1).

2. METODOLOGIA

2.1 Búsqueda aleatoria repetitiva

En esta sección se describe el algoritmo básico de la RSS. Se desea encontrar la solución del problema min f(x) donde x es un vector de N × 1; y f() es una función no lineal tal que 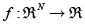. Sea x_l el mejor punto encontrado hasta la k-ésima iteración; en la RSS, al igual que muchos otros algoritmos de optimización, la siguiente solución tentativa, x_c, se calcula como:

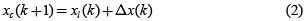
con:

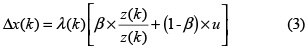
Donde z(k) es un vector que guarda la historia de las direcciones exitosas que han dado como resultado la minimización de f(). u es un vector aleatorio de magnitud unitaria. β∈(0;1) es un factor de ponderación que combina la dirección de minimización de la iteración anterior con una dirección aleatoria (u). En la figura 2 se ilustra gráficamente el proceso de cálculo: la flecha gris punteada representa (1 – β × u y la flecha gris continua representa β × z / z; la dirección resultante se obtiene como la suma de estos dos vectores. Si β es muy cercano a la unidad, Δx(k) tiene, prácticamente, la misma dirección de la iteración anterior, la cual está dada por z(k); y si β es muy cercano a cero, entonces la dirección de Δx(k) es aleatoria, ya que solo es determinada por u. Es así, como el parámetro β puede entenderse como un factor que controla la dirección de búsqueda.

Las ecuaciones (2) y (3) se aplican repetidamente hasta que se obtiene un punto candidato con f(x_c(k + 1)) < f(x_l); en este último caso, se optimiza el tamaño de paso, λ, en la dirección de Δx(k). Una vez se ha encontrado un punto de mínima a lo largo de la dirección de Δx(k), se procede a actualizar el vector de dirección:

Donde γE(0;1) es un factor de ponderación definido por el usuario, de tal forma, que la nueva dirección de búsqueda es una ponderación de las direcciones pasadas. Cuando γ tiende a cero, solo se tiene en cuenta la dirección exitosa en la iteración actual, descartando las direcciones exitosas en iteraciones anteriores.

El algoritmo es esquematizado en la figura 3. El proceso de optimización es realizado para un máximo de K iteraciones. En la línea 03, la función aleatorio(N) genera un vector de magnitud unitaria cuyos elementos se encuentran en el intervalo [0;1]. El tamaño de paso, λ, es iniciado en un valor fijado por el usuario; cada vez que se obtiene un mejor punto, el tamaño de paso es amplificado (línea 09), pero si no se obtiene un mejor punto, el tamaño es disminuido (línea 12); es necesario controlar el tamaño de paso mínimo para evitar que se haga cero o sea muy pequeño (línea 13). En la versión del algoritmo presentado en la figura 3, no se realiza la búsqueda del mínimo exacto en la dirección de Δx; la razón es que tamaños de paso muy grandes pueden tener efectos negativos en el algoritmo, ya que podría estarse alejando del óptimo global.

2.2 Modificación propuesta

La modificación propuesta consiste en reemplazar los parámetros constantes γ y β, que son fijados por el usuario en el algoritmo original, por valores generados usando un mapa caótico; en esta investigación se usa la parábola logística definida en (1). De la línea 03 a la línea 06 de la figura 4 se introduce la modificación propuesta. En las líneas 04 y 06 se introducen condicionales para verificar que las variables β y γ no tomen valores que generen un ciclo periódico.

3. RESULTADOS OBTENIDOS Y DISCUSIÓN

Para analizar el comportamiento del algoritmo propuesto, se utilizaron cuatro funciones de prueba que tienen un único mínimo global. En la tabla 1, se presenta la definición de cada función, la ubicación del óptimo global, el valor de la función en el óptimo global, y el rango de búsqueda para cada una de las funciones utilizadas.

En este estudio, se realizaron 50 corridas con puntos de arranque generados aleatoriamente en el rango de búsqueda definido en la tabla 1 para cada función. Se realizaron corridas para N = 10, 20 y 30 dimensiones. Cada corrida se limitó a un número máximo de iteraciones, dado por la siguiente ecuación:

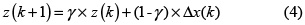
Para el caso del algoritmo original (RRS), se tomó el conjunto de los mejores valores de γ y β para cada función de prueba por medio de un proceso de tanteo. Para el caso del algoritmo modificado (RRS caótico), los parámetros se hallaron con el mapa caótico (1).

En la tabla 2 se presentan los resultados obtenidos al aplicar el algoritmo RRS y el algoritmo RRS caótico a las funciones de prueba mencionadas anteriormente. La columna ''Mejor valor f'' es el menor valor encontrado para la función objetivo en las 50 corridas realizadas. La columna ''Valor promedio f'' es el valor esperado de los punto de mínima encontrados en cada una de las 50 corridas. ''Desviación estándar'' es la desviación estándar de los puntos de mínima encontrados.

Para casi todos los casos considerados, el algoritmo propuesto fue capaz de encontrar un óptimo global de mejor calidad que el obtenido usando RRS. Igualmente, el algoritmo propuesto converge a mejores puntos que el RSS, lo que se evidencia en un mejor valor del promedio de f(). Finalmente, la dispersión de los puntos obtenidos es mucho más baja que la obtenida para el RSS, confirmado la conclusión anterior.

4. CONCLUSIONES

En este artículo se presentó una nueva metodología de optimización llamada ''Búsqueda Aleatoria Repetitiva basada en caos'', desarrollada a partir de un método estocástico directo y mapas caóticos. De los resultados presentados se concluye que la metodología propuesta converge a mejores puntos óptimos que la búsqueda aleatoria repetitiva tradicional, para los ejemplos presentados. La ventaja del método propuesto es que evita que el usuario fije los parámetros del algoritmo, ya que estos evolucionan dinámicamente al introducir el mapa caótico.

Como un trabajo a futuro, es necesario evaluar el desempeño del algoritmo ante el uso de otros mapas caóticos, e incluso, si los parámetros de la técnica se muestrean aleatoriamente en cada iteración usando simulación de Monte Carlo; igualmente, es necesario investigar esquemas alternativos para el cálculo de (tamaño de paso), como por ejemplo, simularlo por medio de un mapa logístico como se está haciendo con γ y β.

Notas:

* Artículo de investigación científica y tecnológica.

REFERENCIAS

[1] Z. Michalewicz, Genetic Algorithms + Date Structures = Evolution Programs, 3rd revised and extended ed., Springer-Verlag, 1996.

[2] M. J. D., Powell, ''An efficient method for finding the minimum of a function of several variables without calculating derivatives'', Computer Journal, vol. 7, pp. 155-162, 1964.

[3] J. Matyas, ''Random optimization'', Automation Remote Control, vol. 26, pp. 246-253, 1965.

[4] R. Hooke. and T. A. Jeeves, (1966) Direct search of numerical and statistical problems'', Journal of the ACM, vol. 8, pp. 212-229, 1966.

[5] J. A. Nelder and R. Mead, ''A simplex method for function minimization'', Computer Journal, vol. 7, pp. 308-313, 1965.

[6] R. J. Kelly and R.F. Wheeling, A digital computer program for optimizing nonlinear functions, Mobil Oil Copr. Research dept., Central Research Dev., Princeton, N,J, July 1962

[7] C.A. Floudas, and P. M. Pardalos, editors. Recent advances in global optimization. Princeton, NJ: Princeton University Press; 1992.

[8] R. Horst and P. M. Pardalos, editors. Handbook ofglobal optimization. Dordrecht: Kluwer Academic Publishers; 1995.

[9] P.M. Pardalos and M. G. C. Resende, editors. Handbook of Applied Optimization. Oxford University Press, New York, 2002.

[10] D. Himmelblau, Applied nonlinear optimization. New York, U. S.: McGraw Hill, 1972.

[11] D. E. Rumelhart and J. L. McClelland, Parallel Distribution Processing: Explorations in the Microstructure of Cognition. Vol. 1: Foundations, MIT Press, Cambridge, MA, USA, 1986.

[12] B. Li and W.-S. Jiang, ''Chaos optimization method and its application'', Control Theory and Application, vol. 14, n.° 4, pp. 613-615, 1997.

[13] B. Li and W.-S. Jiang, ''Optimizing complex function by chaos search'', Cybernetics and Systems, vol. 29, n.° 4, pp. 409–419, 1998.

[14] C. Choi and J. J. Lee, ''Chaotic local search algorithm'', Artificial Life and Robotics, vol. 2, n.° 1, pp. 41-47, 1998.

[15] M. S. Tavazoei and M. Haeri, M. ''An optimization algorithm based on chaotic behavior and fractal nature'', Journal of Computational and Applied Mathematics, vol. 206, n.° 2, pp. 1070-1081, 2007.

[16] D. Yang, G. Li and G. Cheng, ''On the efficiency of chaos optimization algorithms for global optimization'', Chaos, Solitons and Fractals, vol. 34, pp. 1366-1375, 2007.

[17] R. Caponetto, L. Fortuna, S. Fazzino and M. G. Xibilia, ''Chaotic sequences to improve the performance of evolutionary algorithms'', IEEE Transactions on Evolutionary Computation, vol. 7, n.° 3, pp. 289-304, 2003.

[18] S.S: Liu and Z. J. Hou, ''Weighted gradient direction based chaos optimization algorithm for nonlinear programming problem'', In: Proceedings of the Fourth World Congress on Intelligent Control and Automation, vol. 3, pp. 1779-1783, 2002.

[19] F. Fazayeli, L. Wang and W. Liu, ''Back-propagation with chaos'', In: Proceedings of the IEEE International Conference on Neural Network and Signal Processing (ICNNSP2008), pp. 5-8, 2008.

[20] S. H. Strogatz, Nonlinear dynamics and chaos. Massachussetts: Perseus Publishing, 2000

[21] L. Chen and K. Aihara ''Globally Searching Ability of Chaotic Neural Networks'', IEEE Transactions on Circuits and Systems- I: Fundamental Theory and Applications, vol. 46, n.° 8, pp. 974-993, 1999.

[22] I. Tokuda, K. Aihara and T. Nagashima, ''Adaptive annealing for chaotic optimization'', Physical Review E, vol. 58, n.° 4, pp. 5157-5160, 1998.

[23] Y. Yong, S. Wanxing and W. Sunan, ''Study of chaos genetic algorithms and its application in neural networks''. In: Proceedings of the IEEE Region 10 Conference on Computers, Communications, TENCON '02, vol. 1, 232-235, 2002.

[24] R. Qi, F. Qian, S. Li and Z. Wang, ''Chaos-Genetic Algorithm for Multiobjective Optimization'', Proc. Intelligent Control and Automation WCICA, vol. 1, pp. 1563 -1566, 2006.

[25] L. Shengsong, H. Zhijian and W. Min, ''A hybrid algorithm for optimal power flow using the chaos optimization and the linear interior point algorithm'', Proceedings of the International Conference on Power System Technology, vol. 2, pp. 793–797, 2002.

[26] M. J. Ji and H. W. Tang, ''Application of chaos in simulated annealing'', Chaos, Solitons & Fractals, vol. 21, pp. 933-941, 2004.

[27] B. Liu, L. Wang, H. Y. Yin, F. Tang and D.X. Huang, ''Improved particle swarm optimization combined with chaos''. Chaos, Solitons & Fractals, vol. 25, n.° 5, pp. 1261-1271, 2005.

[28] T. Xiang, X. Liao and K. Wong, ''An improved particle swarm optimization algorithm combined with piecewise linear chaotic map'', Applied Mathematics and Computation, vol. 190, n.° 2, pp. 1637-1645, 2007.

[29] S. Changzhi, C. Zhifei and L. Hongmei, ''Chaotic optimization and Taboo search algorithms for design of underwater thruster motor'', Electrical Machines and Systems, ICEMS 2003, Sixth International Conference on, vol. 1, n.° 1, pp. 149- 152, 2003.

[30] J. D. Velásquez, ''An Enhanced Hybrid Chaotic Algorithm using Cyclic Coordinate Search and Gradient Techniques'', Revista de Ingenieria Universidad de los Andes, vol. 43, pp. 45-53, 2010.

[31] J. D. Velásquez, ''R-chaosoptimiser: an optimiser for unconstrained global nonlinear optimization written in R language for statistical computing'', Ingeniería e Investigación, vol. 31, n.° 3, pp. 50-55, 2011.