ARTÍCULO ORIGINAL

ESTIMACIÓN DE LOS PARÁMETROS DEL MODELO NO LINEAL DE PROMEDIOS MÓVILES USANDO LA METAHEURISTICA DE-PSO^*

ESTIMATION OF THE NONLINEAR MOVING AVERAGE MODEL PARAMETERS USING THE DE-PSO META-HEURISTIC

^** Estudiante, Doctorado en Ingeniería - Sistemas, Universidad Nacional de Colombia, Medellín, Colombia. Profesora asistente de la Universidad EAFIT (sede Medellín, Colombia). Dirección de correspondencia: Universidad EAFIT. Departamento de Ciencias Básicas. Escuela de Ciencias y Humanidades. Medellín, Colombia. Correo electrónico: mcogollo@eafit.edu.co

^*** Doctor en Ingeniería, Área de Sistemas Energéticos, Universidad Nacional de Colombia, Medellín, Colombia (2009); Magíster en Ingeniería de Sistemas, Universidad Nacional de Colombia, Medellín, Colombia (1997); Profesor Asociado de la Universidad Nacional de Colombia (sede Medellín, Colombia). Dirección de correspondencia: Universidad Nacional de Colombia. Facultad de Minas. Medellín, Colombia. Correo electrónico: jdvelasq@unal.edu.co.

^**** Doctora en Ingeniería de Caminos, Canales y Puertos, Universidad Politécnica de Valencia, Valencia, España (1999). Profesora Asociada de la Universidad Nacional de Colombia (sede Medellín, Colombia). Dirección de correspondencia: Universidad Nacional de Colombia. Facultad de Minas. Medellín, Colombia. Correo electrónico: gpjarami@unal.edu.co

Recibido: 18/02/2012

Aceptado: 07/05/2013

RESUMEN

La extensión teórica de los modelos lineales de promedios móviles al caso no lineal es directa y sencilla. Sin embargo, el uso práctico de los modelos no lineales de promedios móviles es limitado debido a la complejidad del espacio de parámetros y la imposibilidad de las establecer derivadas analíticas de la función de estimación. En este artículo, se evalúa el uso del algoritmo híbrido Evolución Diferencial-Optimización del Enjambre de Partículas para calcular los parámetros óptimos del modelo no lineal de promedios móviles. Los resultados obtenidos muestran que la técnica meta-heurística utilizada es capaz de calcular con mayor precisión los valores de los parámetros del modelo en comparación con los algoritmos tradicionales. Este hallazgo nos alienta a explorar el uso de las meta-heurísticas en la estimación de los parámetros de otros modelos no lineales de promedios móviles.

PALABRAS CLAVE

Series de tiempo no lineales; métodos no paramétricos; finanzas; calibración; modelos econométricos; optimización no lineal.

ABSTRACT

Theoretical extension of the linear moving average models to the nonlinear case is direct and straightforward. However, the practical use of nonlinear moving average models is limited because of complexity of the parameters space and the impossibility of establishing the analytic derivate of estimation function. In this article, we evaluate the use of the Differential Evolution – Particle Swarm Optimization hybrid algorithm for calculating the optimal parameters of the nonlinear moving averages model. Obtained results show that the used meta-heuristic technique is able to calculate with more accuracy the values of the parameters of the model in comparison with the traditional algorithms. This finding encourages us to explore the use of meta-heuristics in the estimation of the parameters of other nonlinear moving average models.

KEY WORDS

Nonlinear time series; Nonparametric methods; Finance; Calibration; Econometric models; Nonlinear optimization.

INTRODUCCIÓN

En el análisis de series de tiempo lineales se emplean modelos que incluyen tanto elementos autorregresivo (AR) como de promedios móviles (MA, por su sigla en inglés). Su fundamentación matemática fue originalmente desarrollada por Yule [1] y Walker [2] en el caso de los modelos AR y por Slutzky [3] en el caso de los modelos MA. Posteriormente, Wold [4] generalizó los trabajos anteriores al introducir el modelo ARMA. No obstante, la popularización de dichas metodologías y la difusión de su uso fueron debidas al trabajo seminal de Box y Jenkins [5]. Estos modelos han sido ampliamente estudiados y empleados exitosamente. En la literatura abundan ejemplos de su uso; véase, por ejemplo [6].

No obstante, una discusión primordial en la literatura técnica es que los modelos lineales son inadecuados ante los comportamientos no lineales que pueden presentar algunas series de tiempo [7]; esta ha sido una de las principales motivaciones para que los modelos de Box y Jenkins hayan sido generalizados y ampliados al campo no lineal; véanse, por ejemplo, las referencias [8, 9].

Sin embargo, la mayor parte de las investigaciones se basan en la especificación de modelos no lineales a partir de los modelos AR y, comparativamente, hay muy pocos desarrollos y experiencias prácticas en el caso de los modelos MA no lineales. Es así, como muchos modelos no lineales ampliamente referenciados en la literatura se pueden considerar como una extensión de los modelos AR; este es el caso, por ejemplo, de algunos tipos de redes neuronales artificiales [10-12] y modelos basados en regímenes [8, 9].

Como ya se dijo, el proceso no lineal de promedios móviles (NLMA) ha sido poco explorado, tanto empírica como teóricamente. Este hecho se debe en parte a la dificultad que se presenta para establecer la invertibilidad del modelo [13]; sin embargo, recientemente Chan y Tong [14] establecieron que existen condiciones bajo las cuales el modelo NLMA puede llegar a ser localmente invertible. Otro motivo del no uso del NLMA, es que los métodos convencionales de optimización para la estimación de sus parámetros óptimos no son aplicables, debido a que no es posible resolver analíticamente la función de verosimilitud que se obtiene (para un caso específico véase [15]).

Robinson [15] propone como solución al problema de la complejidad de la estimación numérica de la función de verosimilitud, realizar su cálculo de manera recursiva usando métodos de optimización que permitan hacer una exploración del espacio de posibles valores de los parámetros del modelo. En la literatura técnica sobre modelos de series de tiempo se observa un uso frecuente de los métodos númericos tradicionales de optimización basados en gradientes (véase [16-18]), pero, las funciones de máxima verosilimitud asociadas a algunos modelos NLMA no son diferenciables analíticamente, el cálculo numérico de las derivadas tiene un gran costo computacional y la supeficie de búsqueda es bastante compleja e irregular. Contrario a esto, se observa la inexistencia del uso de las técnicas metaheurísticas como alternativas para la estimación de los parámetros óptimos de dichos modelos. De tener éxito estas técnicas en el proceso de estimación del NLMA, no solo se eliminarían los problemas que surgen cuando se aplican los métodos núméricos tradicionales basados en gradientes, sino que también se sentarían las bases para extender dichas metodologías de optimización a otros modelos no lineales que presentan las mismas dificultades en el proceso de estimación.

Consecuentemente con lo anterior, el objtivo de este trabajo es evaluar si la metodología híbrida DE-PSO –que está basada en las técnicas metaheurísticas de Evolución Diferencial y de Optimización del Enjambre de Partículas– permite la estimación de los parámetros óptimos del modelo NLMA.

La organización del documento es como sigue: en la sección 2 se plantean formalmente el modelo NLMA y las versiones que se han propuesto de él hasta la fecha. En la sección 3 se detalla la metodología de estimación propuesta. En la sección 4 se examina la viabilidad de la metodología propuesta a través de un caso de aplicación, y en el sección 5 se exponen las conclusiones.

1 MATERIALES Y MÉTODOS

1.1 Modelo no lineal de promedios móviles

En el modelo no lineal de medias móviles de orden q o NMLA(q), el valor actual de la serie de tiempo, y_t, es una función no lineal y conocida, h(), de los q shocks pasados, {ε_t–1, ..., ε_t–q}, y el shock actual, ε_t:

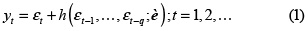
donde θ representa el vector de parámetros de la función h(). Se supone que {ε_t} es una secuencia de variables aleatorias independientes e idénticamente distribuidas (i.i.d.) con media cero y varianza (idéntica) finita.

Dependiendo de la forma que adopte la función h(), se han propuesto los siguientes modelos de promedios móviles:

• Modelo MA(q) convencional : Cuando h() es especificada como una función lineal.

• Modelo polinomial de medias móviles [15]: Con h() definida como una función polinomial y q = 1:

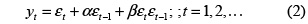
• Modelo asimétrico de medias móviles (asMA, por su sigla en inglés) [16]:

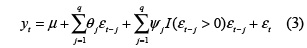
donde I(x) es la función indicadora que toma el valor de la unidad para x ≥ 0 y cero en el caso contrario.

• Modelo no lineal de medias móviles con respuesta con largo alcance [17]: se obtiene al permitir un número infinito de rezagos, es decir, q → ∞:

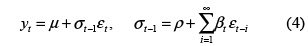
• Modelo no lineal de medias móviles integrado [18]: cuando el impacto a largo plazo de cada innovación es estocástico y variable en el tiempo. Se asume que q = 1.

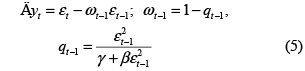
1.2 Estimación de parámetros

Los métodos de estimación de θ en los modelos NLMA se han aplicado bajo el supuesto de normalidad, bien sea de los shocks o de la variables respuesta. Básicamente se han considerado tres métodos para la estimación de los valores óptimos del vector de parámetros θ: máxima verosimilitud (MLE, por su sigla en inglés), método de los momentos (MM) y pseudomáxima verosimilitud (pseudo-MLE).

Bajo el supuesto general de normalidad de {ε_t} es posible considerar estimaciones vía MLE de θ. Sin embargo, como lo indica Robinson [15], la función de verosimilitud resultante es intratable analíticamente, en el sentido que solo puede calcularse recursivamente y, más aún, esto hace muy difícil su manejo matemático para desarrollar propiedades estadísticas asintóticas de los estimadores. Es por ello que Robinson [15] propone la estimación vía MM, basado en los momentos de segundo y tercer orden de y_t, cuyas propiedades distribucionales asintóticas pueden ser establecidas. Si bien, y aunque este método produce estimadores consistentes, las ecuaciones involucradas no poseen una solución explícita, y para su solución es necesario emplear técnicas numéricas de optimización. Por otra parte, Robinson y Zaffaroni [17] emplean la estimación vía pseudo-MLE, bajo el supuesto de que {y_t} tiene una distribución normal. Sin embargo, y al igual que en los otros métodos, se requiere hacer uso de técnicas numéricas de optimización.

En general, en los métodos MLE y pseudo-MLE, el estimador de interés es:

donde Q_T(θ) representa el logaritmo de la función de verosimilitud o pseudoverosimilitud, según el método.

Un problema común a todos los métodos de estimación aquí mencionados, es el hecho de que los shocks {ε_t} no son observables directamente, lo cual impide que ellos puedan usarse como variables de entrada del modelo, tal como se hace en los modelos AR [19]. Este hecho, junto con la complejidad del proceso de estimación de los parámetros, es lo que ha limitado el uso práctico de los modelos NLMA.

1.3 Metaheurística DE-PSO

Tal como se ha planteado en la sección anterior, las técnicas comúnmente utilizadas para la estimación de los valores óptimos de los parámetros en modelos NLMA, así como las características particulares de dichos modelos, han impuesto limitantes prácticas sobre su difusión y uso. Es así como surge la necesidad de desarrollar nuevas técnicas de estimación o explorar las ya existentes en otras áreas del conocimiento, con el fin de superar las dificultades ya enunciadas. Esta es nuestra motivación para evaluar el desempeño de la metaheurística DE-PSO.

La idea básica de una metaheurística es implementar una estrategia de alto nivel que usa diferentes métodos para explorar el espacio de búsqueda (en este caso, el espacio de valores del vector de parámetros θ). Su idea básica es combinar diferentes métodos heurísticos en un nivel superior para conseguir una exploración del espacio de búsqueda de forma eficiente y efectiva.

En este tipo de técnicas es especialmente importante el correcto equilibrio (generalmente dinámico) que haya entre la exploración y la explotación del espacio de búsqueda. La exploración se refiere a la evaluación de soluciones en regiones distantes en el espacio de búsqueda (de acuerdo a una distancia previamente definida entre soluciones), mientras que la explotación se refiere a la exploración minuciosa de soluciones en regiones acotadas y pequeñas, donde hay una alta posibilidad de encontrar el punto de óptima. Al mantener este equilibrio se pueden identificar rápidamente regiones de interés (exploración) para luego concentrar el proceso de búsqueda en ellas (explotación).

Dentro de las metaheurísticas se destacan dos técnicas: la Optimización de Enjambre de Partículas (PSO, por su sigla en inglés), la Evolución Diferencial (DE, por su sigla en inglés). El PSO está inspirado en el comportamiento social del vuelo de las bandadas de aves. Este algoritmo mantiene un conjunto de tamaño fijo de soluciones, llamadas partículas, que son inicializadas aleatoriamente en el espacio de búsqueda. Cada partícula posee una posición y una velocidad que cambia conforme avanza la búsqueda. En el movimiento de una partícula influye no solo su historia de velocidades y posiciones sino también las de las partículas que conforman su vecindario y que encontraron buenas soluciones.

La DE es una técnica estocástica de búsqueda directa que no requiere calcular derivadas de la función a optimizar. En este algoritmo, las variables se representan mediante vectores de números reales. La población inicial siempre es de un tamaño fijo y se genera de forma aleatoria. Para llevar a cabo una nueva solución, es necesario seleccionar aleatoriamente tres individuos de la población; uno de ellos es el llamado vector base que se perturba con el vector diferencia de los otros dos vectores. Si el vector resultante es mejor que el padre, entonces lo reemplaza. De otra forma, se retiene al padre, al menos, una generación más.

En esta investigación se estiman los parámetros del modelo NLMA empleando el algoritmo híbrido DE-PSO [20] que combina los algoritmos de Evolución Diferencial y Optimización de Enjambre de Partículas. El pseudocódigo del algoritmo híbrido se muestra en la figura 1.

Nótese que se inicia como el algoritmo habitual de DE hasta el punto donde se genera el vector base. Si el vector base es mejor que el vector objetivo correspondiente, entonces se incluye en la población. De lo contrario el algoritmo entra en la fase del PSO y genera un nuevo candidato solución con la velocidad del cúmulo de partículas y las ecuaciones de actualización de posiciones, con la esperanza de encontrar una mejor solución. El método se repite iterativamente hasta que el valor óptimo se alcanza. La inclusión de la fase del PSO crea una perturbación en la población que, a su vez, ayuda a mantener la diversidad de la población y la producción de una solución óptima [21].

Se encuentra una nueva partícula usando las ecuaciones de actualización de velocidades y posición del PSO.

Se denota la partícula como

TX=(tx₁,tx₂,...,tx_D) //

Para j=1 to D (dimensión)

v_ij,g+1=w*v_ij,g+c₁r₁(P_ij,g-x_ij,g)+ c₂r₂(P_gj,g-x_ij,g)

tx_ij=x_ij,g+v_ij,g+1

Fin

Si (f(TX_i) < f(X_i,g)) entonces

X_i,g+1=TX_i

Sino

X_i,g+1=X_i,g

Fin

Fin

Fin

1.4 Descripción del experimento

Para examinar la viabilidad del uso del algoritmo DE-PSO en la estimación de parámetros óptimos, se utilizó el modelo descrito en (7) –el cual fue empleado por Burges y Refenes [19] para ejemplificar el uso de modelos NLMA– y pertenece a la clase del NLMA polinomial:

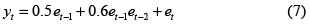
donde e_–1 = e_–2 = 0, y y₀ = e₀ = rand( ). Siendo rand( ) un número aleatorio uniforme entre cero y la unidad.

A partir de (7) se generaron series de tiempo de 400 observaciones, asumiendo que e_t ˜ N(0,1); t = 1,2, ..., 400. Burges y Refenes [19] establecen que esta serie tiene no sólo propiedades similares a las de los cambios en los precios activos financieros, sino también un aspecto similar al de muchas series financieras reales.

Para el algoritmo se emplearon los siguientes parámetros, a partir de los resultados reportados por Hvass [22, 23]

• Tamaño de población: N=13 partículas.

• Probabilidad de recombinación: 0,745.

• Factor de mutación: 90,96%.

• Tasa de aprendizaje cognitivo: 2,8.

• Tasa de aprendizaje social: 1,3.

• Velocidad máxima: 1,2.

• Factor de inercia: 1,2.

Con el fin de examinar el desempeño del algoritmo para estimar los parámetros de modelos no lineales convencionales se consideraron dos variantes para la experimentación:

1. Si las innovaciones son variables determinísticas. En este caso se estimarían los parámetros de un modelo no lineal cuyas variables de entrada serían las innovaciones.

2. Si las innovaciones son variables aleatorias. Este constituye nuestro caso de mayor interés y en él se consideran errores que se actualizan en el tiempo a medida que se van variando los parámetros durante el proceso de optimización.

En los dos casos, el problema de optimización considerado es:

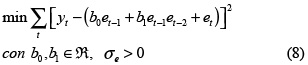
y para el cual θ = {b₀, b₁]'.

2 RESULTADOS Y DISCUSIÓN

Los resultados numéricos encontrados para cada caso, después de realizar 100 realizaciones del algoritmo DE-PSO se muestran en las tablas 1 y 2, respectivamente. Las tablas constan de 6 columnas. En la columna 1 se muestran los parámetros y función objetivo para las que se hallaron las siguientes estadísticas básicas (con base en 100 realizaciones cada una de máximo 400 iteraciones): promedio (columna 2), desviación estándar (columna 3), coeficiente de variación estimado (cve) (columna 4), valor mínimo (columna 5) y valor máximo (columna 6).

En ambos casos, se observa que las estimaciones obtenidas para los parámetros son muy homogéneas, pues tienen un coeficiente de variación muy por debajo del 33 %. Asimismo, el valor promedio de las estimaciones es cercano a los valores ideales (0,5 para b₀ y 0,6 para b₁). Con respecto a la función a minimizar (8) se encuentran un cve superior al 33 %, lo cual era de esperarse debido a la generación aleatoria que se hace al inicio del algoritmo híbrido. Sin embargo, después de varias iteraciones esta función tiende a estabilizarse como se muestra en las figuras 1 y 2. Con respecto a las mejores estimaciones (en términos de minimización la función objetivo) se encontró lo siguiente para cada caso evaluado:

Caso 1: b₀ = 0,4998, b₁ = 0,5998, σ² = 2,2466 × 10^–17

Caso 2: b₀ = 0,4995, b₁ = 0,5991, ² = 2,4461 × 10^–4.

Es de resaltar, que con esta técnica se logra una ganancia significativa con respecto al resultado hallado por Burges y Refenes [19] quienes al considerar un NLMA(2) lograron ² = 0,692.

Adicionalmente, a partir de las realizaciones obtenidas para el caso 1 se observa que el algoritmo es capaz de hallar las estimaciones óptimas de los parámetros en menos de 20 iteraciones (ver figura 1). Para el caso 2, es necesario un mayor número de iteraciones (cercanas a 100); sin embargo, el costo computacional no es tan alto teniendo en cuenta la complejidad de este último proceso de estimación.

3 CONCLUSIONES

Se muestra el uso de las técnicas metaheurísticas en el proceso de estimación de parámetros de modelos de series de tiempo no lineales, que son difíciles de estimar con los métodos convencionales. Se realiza un caso de aplicación en el que se obtiene una ganancia significativa en cuanto a la disminución del σ² y el sesgo de los estimadores.

Notas:

* Artículo de investigación científica y tecnológica.

REFERENCIAS

[1] G. U. Yule, ''Why do we sometimes get nonsense-correlations between time series? A study in sampling and the nature of time series'', Journal of the Royal Statistical Society, vol. 89, pp. 1-64, 1926.

[2] A. M. Walker, ''On the periodicity in series of related terms'', Proceedings of the Royal Society of London A, vol. 131, pp. 518-532, 1931.

[3] E. Slutzky, ''The summation of random causes as the source of cyclic processes'', Econometrica, vol. 5, pp. 105-146, 1937.

[4] H. Wold, A study in the analysis of stationary time series, 2a ed., Stockholm: Almqvist & Wiksell, 1954, 236 p.

[5] G. Box, y G. M. Jenkins , Time-Series analysis: forecasting and control. San Francisco, CA: Holden –Day, 1970,575 p.

[6] J. D. Velásquez y S. Aguilar, ''Un análisis de la dinámica de largo plazo de la UVR'', Revista Ingenierías Universidad de Medellín, vol. 10, n.° 18, pp. 97-106, 2011.

[7] M. P. Clements et al., ''Forecasting economic and financial time-series with non-linear models'', International Journal of Forecasting, vol. 20, pp.169-183, 2004.

[8] C. Granger y T. Teräsvirta, Modeling Nonlinear Economic Relationships. Oxford University Press, 1993, 187 p.

[9] P. H. Frances y D. van Dijk, Nonlinear time series models in empirical finance, 1a ed., Cambridge University Press, 2000, 298 p.

[10] H. White, ''An additional hidden unit test for neglected nonlinearity in multilayer feedforward networks'', Proceedings of the International Joint Conference on Neural Networks. vol 2, pp. 451-455, 1989.

[11] T.H. Lee et al.,'' Testing for neglected nonlinearity in time series models'', Journal of Econometrics, vol. 56, pp. 269 - 290, 1993.

[12] T. Teräsvirta et al., ''Power of the neural network linearity test'', Journal of Time Series Analysis, vol. 14, n.° 2, pp. 209 - 220, 1993.

[13] J. De Gooijer, y K. Brännäs, ''Invertibility of non-linear time series models'', Communications in Statistics - Theory and Methods, vol. 24, pp. 2701–2714, 1995.

[14] K. Chan y H. Tong, ''A note on the invertibility of nonlinear ARMA models'', Journal of Statistical Planning and Inference, vol.140 , pp. 3709–3714, 2010.

[15] P. M. Robinson, ''The estimation of a nonlinear moving average model'', Stochastic Processes and their Applications, vol. 5, pp. 81-90, 1977.

[16] W. E. Wecker, ''Asymmetric time series'', Journal of the American Statistical Association, vol. 76, pp.16-21, 1981.

[17] P. M. Robinson y P. Zaffaroni, ''Modelling nonlinearity and long memory in time series'', Fields Institute Communications, vol. 11, pp. 161-170, 1997.

[18] R. F. Engle y A. Smith, ''Stochastic permanent breaks'', Review of Economics and Statistics, vol. 81, pp. 553- 574, 1999.

[19] A. Burgess y A. P. Refenes, ''Modelling non-linear moving average processes using neural networks with error feedback: An application to implied volatility forecasting'', Signal Processing, vol. 74, pp. 89-99, 1999.

[20] M. Pant, et al., ''DE-PSO: a new hybrid meta-heuristic for solving global optimization problems'', New Mathematics and Natural Computation, vol. 7, n.° 3, pp. 363-381, 2011.

[21] R. Thangaraj, et al., ''Particle swarm optimization: Hybridization perspectives and experimental illustrations'', Applied Mathematics and Computation, vol. 217, pp. 5208–5226, 2011.

[22] M. Hvass, ''Good Parameters for Differential Evolution'', Technical Report no. HL1002, 2010.

[23] M. Hvass, ''Good Parameters for Particle Swarm Optimization'', Technical Report n.° HL1001, 2010.