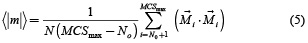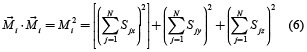ARTÍCULO ORIGINAL
INTERFAZ GRÁFICA COMO UNA HERRAMIENTA EN LA SIMULACIÓN DE PROPIEDADES DE MANGANITAS Re2/3A1/3MnO3 EMPLEANDO EL MÉTODO DE MONTE CARLO Y EL MODELO DE HEISENBERG
GRAPHICAL INTERFACE AS A TOOL IN SIMULATION OF MAGNETIC PROPERTIES OF Re2/3A1/3MnO3 MANGANITES WITH MONTE CARLO METHOD AND HEISENBERG MODEL
H. Barco-Ríos*; E. Rojas-Calderón**; E. Restrepo-Parra***
* Máster en Física. Departamento de Física y Química, Universidad Nacional de Colombia, sede Manizales. E-mail: hsbarcor@unal.edu.co
** Máster en Economía del Medio Ambiente y Recursos. Departamento de Física y Química, Universidad Nacional de Colombia, sede Manizales. E-mail: erojasca@unal.edu.co
*** Doctora en Ingeniería - Línea Automática, Departamento de Física y Química, Universidad Nacional de Colombia, sede Manizales. E-mail: erestrepopa@unal.edu.co
Recibido: 07/02/2012
Aceptado: 07/05/2013
RESUMEN
Las interfaces gráficas son útiles para especificar y examinar estructuras químicas y propiedades físicas de materiales. En este artículo se presenta el software SIMMON (Simulación de propiedades magnéticas de manganitas) como un programa de visualización cuyo objetivo es mostrar la magnetización, la susceptibilidad magnética, la energía, el calor específico, los ciclos de histéresis y la resistividad de materiales magnéticos. Estas propiedades pueden ser obtenidas a partir de la simulación de diferentes manganitas del tipo Re2/3A1/3MnO3, donde Re son iones de una tierra rara metálica como La, Nd y Pr con valencia 3+, los cuales se enlazan con iones Mn3+–3d4 y A es una tierra alcalina con valencia 2+ tal como Ba, Ca, Sr, entre otras, enlazadas con Mn4+–3d3. En estas simulaciones se emplea el método Monte Carlo combinado con el algoritmo de Metrópolis y el modelo de Heinsenberg.
PALABRAS CLAVE
Manganitas, magnetización, histéresis, resistividad, Monte Carlo.
ABSTRACT
The graphics interface is useful in specifying and examining chemical structures and physical properties. In this scientific and technological research paper, the SIMMON (MMSP - Manganite magnetic simulation properties) software is presented, as a visualization program, that allows to observe, the magnetization, susceptibility, energy, specific heat, the hysteresis loops and the resistivity of magnetic materials. This properties can be obtained from the simulation of different manganites Re2/3A1/3MnO3, where Re is a rare earth metal ions as La, Nd and Pr with valence 3+, which are bonded with Mn3+–3d4 ions and A is a 2+ alkaline earth ion such as Ba, Ca, Sr, among others, bonded with Mn4+–3d3. The based method for the simulations is Monte Carlo combined with Metropolis algorithm and Heisenberg model.
KEY WORDS
Manganites, magnetization, hysteresis, resistivity, Monte Carlo
INTRODUCCIÓN
Las representaciones gráficas de las estructuras de los materiales y sus diferentes propiedades físicas son importantes para llevar a cabo simulaciones del comportamiento de la materia a escala atómica. Desde tiempo atrás, la comunidad científica ha desarrollado estudios teóricos de diferentes propiedades físicas y químicas de la materia como es el caso de enlaces químicos, estructura química, propiedades mecánicas, eléctricas y magnéticas, entre otras. Sin embargo, anteriormente existían muchas limitaciones debido a que las herramientas computacionales no estaban lo suficientemente desarrolladas [1]. Posteriormente, los grandes avances de los sistemas computacionales y su fácil accesibilidad hicieron posible el desarrollo de modelos de primeros principios (ab-initio), incrementando el interés en áreas como la química, la física y la ciencia de los materiales [2]. El desarrollo de software de simulación, disponible actualmente para estudios de propiedades de sistemas moleculares y cristalinos basados en mecánica cuántica, ha fomentado su utilización por usuarios no especializados tales como investigadores experimentales [3]. Por estas razones las interfaces gráficas, que permiten simulaciones más intuitivas y fácil análisis de los datos entregados por el computador, son en la actualidad herramientas de gran valor.
Con respecto a las propiedades magnéticas, existe en la literatura una gran cantidad de reportes de modelos y simulaciones de materiales tales como magnetitas y manganitas, entre otras. En muchos de estos trabajos se emplea el método de Monte Carlo combinado con los modelos de Ising y Heisenberg [4]. Normalmente estas simulaciones tienen códigos muy extensos, y únicamente el experto o la persona que construyó el programa pueden usarlo. Sin embargo, no es común encontrar reportes de interfaces gráficas que hagan más fácil el cálculo de las propiedades magnéticas.
Por esta razón, en este documento se presenta el desarrollo de una interfaz gráfica que permite determinar propiedades tales como magnetización, susceptibilidad magnética, calor específico, ciclos de histéresis y transporte eléctrico en manganitas. La interfaz gráfica fue desarrollada empleando el software Visual Basic. El algoritmo implementado permite determinar las propiedades magnéticas en función de la temperatura y del campo magnético. Con este fin se empleó el método de Monte Carlo, el algoritmo de Metrópolis y el modelo de Heinsenberg.
1 MATERIALES Y MÉTODOS
1.1 Modelo teórico
Las manganitas del tipo Re2/3A1/3MnO3 (Re= La, Nd, Pr y A=Ca, Sr, Ba) son compuestos ferromagnéticos por debajo de la temperatura de transición o temperatura de Curie (Tc). Estos compuestos se caracterizan por tener tres tipos de iones: Mn4+ (espín 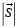 =3/2), que se enlazan con los iones A2+, Mn3+eg y Mn3+eg' (espín
=3/2), que se enlazan con los iones A2+, Mn3+eg y Mn3+eg' (espín 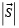 =2) que se relacionan con los iones Re3+. Estos materiales tienen estructura tipo perovskita (red cúbica simple) para el caso ideal con un número de coordinación de seis [5]. En la literatura existen muchas simulaciones teóricas que emplean diferentes métodos como dinámica molecular, cálculos ab-initio y Monte Carlo [6]. Para el caso de la simulación presentada en este trabajo se empleó una organización periódica de iones como la propuesta por Hotta et al. [6]. El modelo empleado se basa en un hamiltoniano tridimensional clásico de Heinsenberg dentro de la primera coordinación magnética. Los iones magnéticos Mn3+eg', Mn3+eg and Mn4+d3 se representan por espines clásicos de Heinsenberg, mientras que el oxígeno, y los iones Re y A se consideran no magnéticos. Los espines interactúan vía parámetros de intercambio dependiendo de la valencia. El hamiltoniano usado en este trabajo está dado por [7]:
=2) que se relacionan con los iones Re3+. Estos materiales tienen estructura tipo perovskita (red cúbica simple) para el caso ideal con un número de coordinación de seis [5]. En la literatura existen muchas simulaciones teóricas que emplean diferentes métodos como dinámica molecular, cálculos ab-initio y Monte Carlo [6]. Para el caso de la simulación presentada en este trabajo se empleó una organización periódica de iones como la propuesta por Hotta et al. [6]. El modelo empleado se basa en un hamiltoniano tridimensional clásico de Heinsenberg dentro de la primera coordinación magnética. Los iones magnéticos Mn3+eg', Mn3+eg and Mn4+d3 se representan por espines clásicos de Heinsenberg, mientras que el oxígeno, y los iones Re y A se consideran no magnéticos. Los espines interactúan vía parámetros de intercambio dependiendo de la valencia. El hamiltoniano usado en este trabajo está dado por [7]:
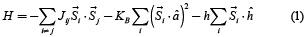
La primera suma representa la interacción entre primeros vecinos con un número de coordinación de seis. El segundo término representa la anisotropía magnetocristalina; el vector unidad 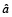 indica la dirección del eje fácil. El tercer término presenta la influencia del campo magnético externo, siendo
indica la dirección del eje fácil. El tercer término presenta la influencia del campo magnético externo, siendo 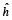 la dirección en la que se aplica dicho campo. Se consideran tres tipos de iones: Mn3+eg'-O- Mn3+eg, Mn3+eg-O-Mn4+d3 y Mn3+ eg'-O-Mn4+d3 con parámetros de intercambio Jab, Jab1 y Jab2. Estos parámetros dependen del tipo de manganita que se desea simular; por ejemplo, para el caso de La2/3Ca1/3MnO3, E. Restrepo et al. [8] reportaron simulaciones de este material al emplear el modelo de Heisenberg, y reproducir la temperatura de Curie Tc (260 K). Los valores numéricos empleados para estos parámetros fueron Jab=4.65 meV, Jab1=7.7 meV y Jab2=1.35 meV. En este caso se empleó el algoritmo de Metrópolis con el fin de obtener las propiedades de equilibrio [3]. Este modelo entonces incluye características propias del material como son el ordenamiento orbital y la mezcla de espines tipo Heisenberg. Por otro lado, aunque la energía elástica es usualmente mayor que la magnética, tal contribución hace parte de un valor constante dentro de la energía interna sin presentar cambios; por lo tanto, los iones se consideran en posiciones fijas, se desprecia la contribución de energía elástica, y se tiene un hamiltoniano puramente magnético.
la dirección en la que se aplica dicho campo. Se consideran tres tipos de iones: Mn3+eg'-O- Mn3+eg, Mn3+eg-O-Mn4+d3 y Mn3+ eg'-O-Mn4+d3 con parámetros de intercambio Jab, Jab1 y Jab2. Estos parámetros dependen del tipo de manganita que se desea simular; por ejemplo, para el caso de La2/3Ca1/3MnO3, E. Restrepo et al. [8] reportaron simulaciones de este material al emplear el modelo de Heisenberg, y reproducir la temperatura de Curie Tc (260 K). Los valores numéricos empleados para estos parámetros fueron Jab=4.65 meV, Jab1=7.7 meV y Jab2=1.35 meV. En este caso se empleó el algoritmo de Metrópolis con el fin de obtener las propiedades de equilibrio [3]. Este modelo entonces incluye características propias del material como son el ordenamiento orbital y la mezcla de espines tipo Heisenberg. Por otro lado, aunque la energía elástica es usualmente mayor que la magnética, tal contribución hace parte de un valor constante dentro de la energía interna sin presentar cambios; por lo tanto, los iones se consideran en posiciones fijas, se desprecia la contribución de energía elástica, y se tiene un hamiltoniano puramente magnético.
En el modelo propuesto tampoco se tiene en cuenta el desplazamiento de los iones debido a la contribución vibracional, ya que de acuerdo con el modelo de Chakravarty et al [9] las constantes de intercambio tienen una dependencia exponencial de la posición atómica, con una distancia de decaimiento del orden típico del radio iónico de las especies que componen el material y que participan en el superintercambio. Esto quiere decir que si los átomos se desplazan una distancia considerable de su posición de equilibrio, la interacción magnética debe cambiar. Sin embargo, teniendo en cuenta que la frecuencia vibracional está relacionada con las masas de los átomos implicados como 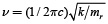 , siendo c la velocidad de la luz, k la constante de fuerza del enlace y mr = m1m2/(m1 + m2) la masa reducida que depende de los dos iones del enlace, que en este caso son el manganeso y el oxígeno (teniendo en cuenta que se tienen estructuras Mn-O-Mn). Debido a que el oxígeno es muy pequeño, la frecuencia de vibración es alta y, por ende, el desplazamiento (que es inversamente proporcional a la frecuencia) es pequeño, lo que permite eliminar cualquier influencia del desorden dinámico o térmico sobre las constantes de intercambio [10].
, siendo c la velocidad de la luz, k la constante de fuerza del enlace y mr = m1m2/(m1 + m2) la masa reducida que depende de los dos iones del enlace, que en este caso son el manganeso y el oxígeno (teniendo en cuenta que se tienen estructuras Mn-O-Mn). Debido a que el oxígeno es muy pequeño, la frecuencia de vibración es alta y, por ende, el desplazamiento (que es inversamente proporcional a la frecuencia) es pequeño, lo que permite eliminar cualquier influencia del desorden dinámico o térmico sobre las constantes de intercambio [10].
Las simulaciones se llevaron a cabo en un proceso de enfriamiento desde una temperatura muy por encima de Tc, iniciando desde un estado de energía con espines orientados aleatoriamente, lo que corresponde a una temperatura infinita. Se consideraron 105 pasos de Monte Carlo por espín, con el fin de obtener las propiedades de equilibrio. Las cantidades de equilibrio termodinámicas básicas obtenidas fueron la energía total, la magnetización por espín, la susceptibilidad magnética, el calor específico y la resistividad. Las muestras fueron construidas empleando condiciones de frontera periódicas en el plano x-y, con el fin de evitar los efectos de borde en los resultados, mientras que en la dirección z se utilizaron condiciones de frontera libre, para tener en cuenta los efectos de superficie [11].
1.2 Método Monte Carlo
Monte Carlo es un método numérico muy empleado para resolver problemas de física estadística. La idea es simular aleatoriamente fluctuaciones térmicas del sistema, pasando de un estado a otro por medio de cadenas de Markov de configuraciones del espacio. Con el fin de encontrar la distribución probabilística, se debe simular el sistema en equilibrio termodinámico en el caso real. Una ventaja de este método es que no se requiere pasar por todos los estados del sistema para determinar los observables. Por esta razón, es necesario escoger los estados que mejor representen el sistema con el fin de disminuir el tiempo de cómputo y los errores estadísticos y correlativos. Esta metodología se denomina muestreo por importancia. Con este fin se escoge un estado µ de acuerdo con su probabilidad de ocurrencia, empleando el formalismo canónico [12].

Donde: Z es la función de partición del sistema β = 1/KBT, con KB como la constante de Boltzmann, T la temperatura y Eµ la energía del estado µ. Otra parte importante es la forma como se lleva a cabo el tránsito de un estado a otro. En este caso se emplean las cadenas de Markov. Este mecanismo permite generar un estado v a partir de un estado µ con probabilidad de cambio P(µ → v), normalizada como 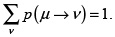 Esta probabilidad debe llenar dos condiciones: (i) no debe variar a través del tiempo y (ii) debe depender solo de las propiedades de los estados µ y v, y de ningún otro. El sistema eventualmente debe converger hacia una secuencia de estados por una probabilidad con distribución de Boltzmann que se dirige hacia el equilibrio de estados. Con el fin de alcanzar este objetivo se deben considerar dos condiciones: (i) la ergodicidad del sistema y (ii) el balance detallado. Para mayor información ver la referencia [13] y las referencias dentro de ella.
Esta probabilidad debe llenar dos condiciones: (i) no debe variar a través del tiempo y (ii) debe depender solo de las propiedades de los estados µ y v, y de ningún otro. El sistema eventualmente debe converger hacia una secuencia de estados por una probabilidad con distribución de Boltzmann que se dirige hacia el equilibrio de estados. Con el fin de alcanzar este objetivo se deben considerar dos condiciones: (i) la ergodicidad del sistema y (ii) el balance detallado. Para mayor información ver la referencia [13] y las referencias dentro de ella.
Los promedios termodinámicos A de un observable A(xi), siendo xi sus coordenadas están dados por:

Con N como el número total de datos empleados para realizar el promedio. Basado en el algoritmo Metrópolis introducido en 1953, el procedimiento es el siguiente [12, 13]
1. Se establece una configuración inicial.
2. Se visita cada sitio dentro de la red tratando de invertir el espín.
3. Se calcula el cambio de energía ΔE para esta inversión.
4. Si ΔE es menor o igual a cero, se acepta la inversión y se regresa al paso 2.
5. Por el contrario, se genera un número aleatorio r en un intervalo [0,1].
6. Si ΔE es positivo, se calcula la expresión W=exp(–ΔE/kBT).
7. Si r ≤ W la inversión es aceptada de lo contrario, se mantiene la contribución inicial.
8. El programa retorna al paso 2 hasta que se visite toda la red.
9. Posteriormente se calculan los observables.
10. Se repiten los pasos 2 al 8 hasta que se obtengan un número suficiente de configuraciones (número total e pasos de Monte Carlo).
11. Se calcula el promedio del ensamble.
Las propiedades obtenidas aquí son energía (E), magnetización por sitio magnético (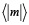 ), calor específico (Cv) y susceptibilidad (χ) [13].
), calor específico (Cv) y susceptibilidad (χ) [13].

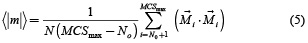
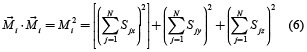

Siendo Sjx,Sjy, Sjz y MCSmax los componentes del espín y el número máximo de pasos de Monte Carlo, respectivamente. Para cada punto de las curvas de simulación se descartan los primeros 104 pasos de Monte Carlo por sitio (N0) y un número igual fue considerado para obtener los promedios.
1.3 Estructura del código
SIMMON consiste de tres módulos (ver figura 1(a)): (1) entrada y procesamiento de datos (2), simulación numérica del hamiltoniano y (3) procesamiento y cálculo de resultados. La figura 1(b) presenta un diagrama de las diferentes propiedades que se pueden calcular con SIMMON. El primer grupo es empleado para determinar las propiedades magnéticas en función de la temperatura, como magnetización, susceptibilidad, energía y calor específico; el segundo módulo permite obtener ciclos de histéresis y el tercero se emplea para determinar las propiedades de transporte eléctrico. Normalmente, SIMMON se puede ejecutar bajo Windows 9X, NT, 2000, Windows XP y windows Vista y se requiere poca memoria (5 MB para un cálculo típico usando 104 pasos de Monte Carlo y 1000 partículas). Los archivos que contienen los resultados tienen un formato ASCII.
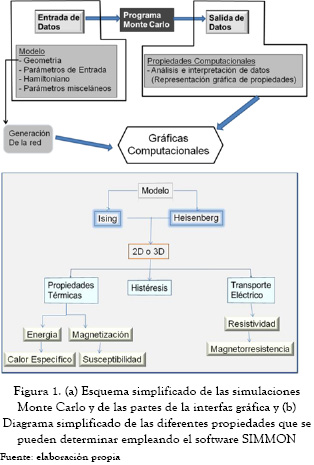
1.3.1 Interfaz gráfica
Las características de la interfaz gráfica son:
– Menú principal para escoger las propiedades a simular.
o Propiedades magnéticas en función de la temperatura.
o Histéresis.
o Resistividad.
– Menú para visualizar, graficar, gravar, limpiar y salir.
– Visualización 2–D y 3–D de las estructuras atómicas periódicas.
– Ventana para la introducción de datos.
– Visualización de la energía y el calor especifico.
– Visualización de la magnetización y la susceptibilidad.
– Visualización de los ciclos de histéresis.
– Visualización de la resistividad y la magnetorresistencia.
– Soporte para la visualización dinámica de los resultados mientras el programa se ejecuta.
La generación de una red cristalina de la manganita La2/3Ca1/3MnO3 se muestra en las figuras 2, 3 y 4 como un ejemplo. SIMMON permite determinar propiedades importantes como temperatura crítica y campo coercitivo.
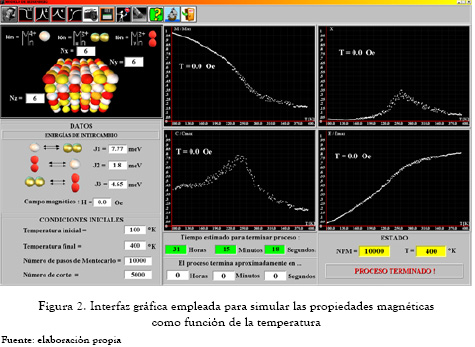
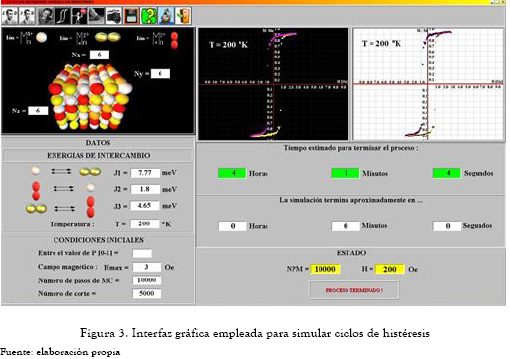
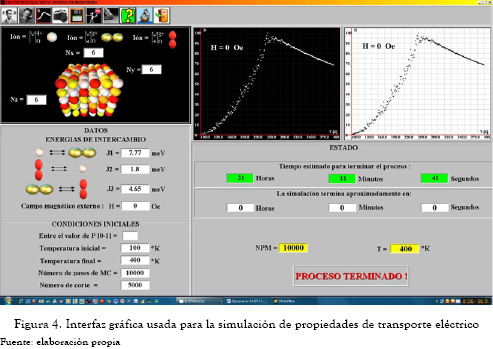
2. RESULTADOS
2.1 Propiedades térmicas
Las figuras 5(a), 5(b) y 5(c) muestran curvas de magnetización, susceptibilidad y calor específico en función de la temperatura para algunos tamaños de muestra escogidos (L=6, 9 y 12 celdas unidad), para un campo magnético externo aplicado igual a cero. En todas las gráficas se observa una fuerte influencia de la temperatura. En las curvas de magnetización, la transición tiende a ser más abrupta a medida que se incrementa el valor de L. Esto se observa aún mejor en las curvas de susceptibilidad, ya que a medida que se incrementa L, el máximo de la curva se corre hacia valores de temperatura mayores, es decir, se presenta un incremento en la temperatura crítica Tc, aproximándose al valor reportado para el bloque (260K). Esta característica es una señal típica del efecto de escalamiento finito [14].
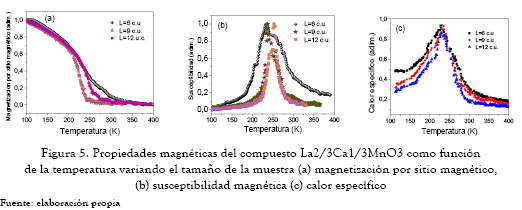
Curvas similares fueron obtenidas por K. H. Ahn et al. [15], para muestras fabricadas empleando métodos de reacción convencionales de estado sólido. Las muestras presentan una transición paramagnética-ferromagnética alrededor de 260K. Otra característica importante observada en las curvas de susceptibilidad es la disminución de su ensanchamiento a medida que se incrementa el tamaño de la muestra. Esto se debe a que la transición entre las fases paramagnética y ferromagnética es más abrupta, a medida que se incrementa L. Un comportamiento simular se observó para el caso del calor específico (figura 5(c)).
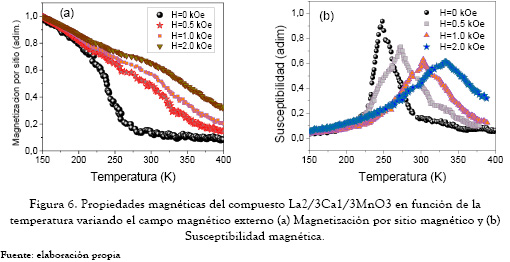
Las figuras 6(a) y 6(b) muestran curvas de magnetización y susceptibilidad magnética en función de la temperatura para diferentes campos magnéticos externos aplicados h. La característica más importante observada en estas curvas es el corrimiento de la transición paramagnética-ferromagnética a medida que el campo externo se incrementa. Esto se debe a que el campo magnético ayuda a la orientación de los espines en su dirección (en este caso se escogió el campo magnético en la dirección x). Normalmente un incremento en la temperatura produce un desorden o entropía; sin embargo, la influencia de un campo magnético externo aplicado produce un efecto que compite con la temperatura, evitando el desorden.
2.2 Ciclos de histéresis
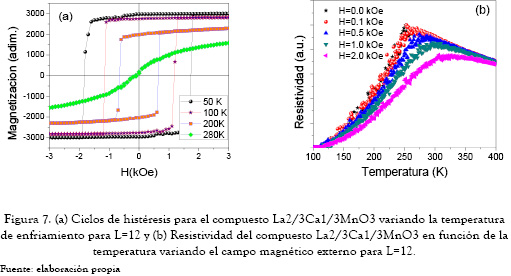
La figura 7(a) presenta ciclos de histéresis correspondientes a muestras de tamaño L=12 y diferentes temperaturas. A partir de esta figura se pueden deducir muchas características importantes. Primero, los ciclos de histéresis muestran formas típicas similares a las reportadas en la literatura para materiales ferromagnéticos del tipo LaCaMnO por debajo de Tc; segundo, a medida que la temperatura se incrementa, el área dentro del ciclo de histéresis tiende a desaparecer. En esta figura, se muestran las curvas para Tc (50, 100 y 200K) y T>Tc (280K). A media que la temperatura se acerca a la temperatura de transición, los ciclos de histéresis presentan un comportamiento paramagnético. Además, a muy bajas temperaturas, el área dentro del ciclo de histéresis se hace más grande. Esto se debe a que a bajas temperaturas, los espines de la muestra prácticamente se congelan, siendo necesario aplicar un campo magnético mayor para girarlos y así desmagnetizar el material.
2.3 Resistividad
La figura 7(b) muestra la resistividad en función de la temperatura para muestras de tamaño L=12 a diferentes campos magnético aplicados. La transición ferromagnética a Tc es indicada por medio de una línea vertical. La curva a un campo magnético igual a cero es una característica de muchas manganitas de ancho de banda intermedio. Como se reporta por otros autores, se observa una bomba en ρ por debajo de Tc y un punto de inflexión en Tc. Además, la altura de la bomba cae cuando se incrementa h. En estos términos, la percolación se puede ver como el paso de un agente a través de un medio irregular, en el sentido de que el agente puede propagarse a través de ciertas regiones, mientras que no puede atravesar otras áreas.
La percolación es uno de los modelos más simples para el caso de sistemas aleatorios, y ha tenido muchas aplicaciones. Esta transición de percolación se define como un fenómeno crítico genuino encontrado en la mecánica estadística del equilibrio [16]. En esta figura se pueden identificar dos regiones: inicialmente se tiene un comportamiento aislante por encima del Tc en el régimen paramagnético al lado derecho de la gráfica. Esto es interesante ya que a medida que la temperatura disminuye, eventualmente se llega a un estado metálico. El comportamiento aislante no se puede explicar por el mecanismo de doble intercambio, en el cual los electrones eg simplemente son dispersados por los espines localizados desordenados, y este mecanismo no es lo suficientemente fuerte como para inducir un comportamiento aislante. Segundo, cerca de Tc, una transición un tanto abrupta ocurre, permitiendo un comportamiento metálico en el régimen ferromagnético del lado izquierdo de la curva. A medida que T tiende a cero, la resistividad converge a un valor un tanto grande de la resistividad. A ambos lados de Tc, la resistividad ρ disminuye exponencialmente. Esto demuestra que la tendencia a disminuir observada experimentalmente en la fase de altas temperaturas no es causada por una fase semiconductora o por una transición metal-aislante como se cree frecuentemente, sino por el número de estados finales disponibles en la dispersión [17]. Un objetivo importante consiste en entender la fenomenología que describe la presencia de las fases eléctricas metálica y aislante al mismo valor de dopaje (x = 1/3), pero dependiendo de la temperatura. En la región ferromagnética-metálica de La1-xCaxMnO3 para 0.21 ≤ x ≤ 0.4, la banda producida por la hibridación de los orbitales eg está menos ocupada que para el caso de x≤0.21; esto es, existe mayor cantidad de huecos, y por lo tanto, los electrones llegan a ser itinerantes. Como resultado, los materiales sufren una transición de la fase aislante a la fase metálica a bajas temperaturas, dependiendo de los valores de dopaje. Ya que las interacciones de doble intercambio requieren que exista un desorden en los iones Mn3+ y Mn4+ así que se generen enlaces Mn3+ –O – Mn4+ a partir de Mn4+ –O – Mn3+, el ordenamiento orbital se produce para la fase metálica. Cuando x =1/3, un mayor número de iones Mn3+ que tienen un único ion Mn4+ como vecino hace que la interacción de doble intercambio sea óptima, y por ende, la temperatura de Curie y la conductividad presenten sus valores máximos
(T ≈ 260 K). Mientras que el sistema a estos niveles de dopaje puede describirse de una forma muy real por la interacción de doble intercambio, las propiedades tipo aislante por encima de la temperatura crítica necesitan de otros factores importantes para su entendimiento. Esto se debe a que las bandas parcialmente ocupadas eg hacen que el sistema sea siempre metálico y la interacción de doble intercambio sea insuficiente. Otros conceptos deben ser introducidos como los presentados por Millis et al. [18], denominado el efecto de polarón bajo Jahn-Teller. Este efecto consiste en tener en cuenta la deformación de los orbitales. Esta deformación es menor para los orbitales eg pertenecientes a los iones Mn4+ comparada con sus iones vecinos Mn3+, causada por el incremento en la temperatura. La energía ganada debido a esta distorsión JT hace que los portadores de carga sean localmente atrapados, así que el sistema se comporta prácticamente como un aislante. Estos resultados son similares a los reportados por diversos autores en la literatura. Por ejemplo, S. Keshri et al. [19] sintetizaron el compuesto La0.67Ca0.33MnO3 en forma de nanopartículas con diámetros entre 50-150 nm, empleando termólisis en una solución acuosa mezclada con polímetros, empezando desde precursores como La2O3 y CaCO3 con una estequiometria apropiada y (CH3COO)2Mn4H2O en agua destilada. Las medidas de resistividad y magnetorresistencia presentaron curvas con un máximo en la temperatura de transición metal-aislante. Para el caso reportado por estos autores, esta transición se produjo a 205 K, una temperatura mucho ¿más o menos? baja que en nuestro caso. Esto se debe a que el efecto de los bordes es mayor en las nanopartículas. T. Zhao et al, [20] reportan el estudio de las propiedades magnéticas de un transistor de campo construido con películas delgadas de LaCaMno y materiales ferroeléctricos. Las curvas de resistividad presentan un incremento a medida que la temperatura se acerca a 260 K en la fase paramagnética, y alcanzan su máximo a dicha temperatura. Por debajo de la temperatura máxima, LCMO llega a la fase ferromagnética y su resistividad comienza a disminuir abruptamente.
En resumen, en este trabajo se presenta una interfaz gráfica para modelar y simular el comportamiento magnético y de transporte eléctrico de materiales como manganitas. Esta interfaz gráfica permite determinar propiedades como magnetización por sitio magnético, susceptibilidad magnética, energía, calor específico, ciclos de histéresis y resistividad. Con el fin de probar el desempeño del software, la manganita La2/3Ca1/3MnO3 fue modelada, reproduciendo su temperatura crítica. Además, se estudió la influencia de parámetros geométricos como tamaño de la muestra en dichas propiedades.
3 AGRADECIMIENTOS
Los autores agradecemos a la Dirección de Investigaciones de la Universidad Nacional de Colombia sede Manizales durante el curso de esta investigación, por su apoyo económico parcial bajo el proyecto 10709 ''Implementación de técnicas de Modelamiento, Procesamiento Digital y simulación para el estudio de sistemas físicos''.
REFERENCIAS
[1] M. Talati, P. K. Jha, J. Mol. Struct. 838 (2007) 227.
[2] H Hauser, Sensors and Actuators A: Phys. 106 (2003) 84.
[3] J. Mazo-Zuluaga, J. Restrepo, Phys. B: Cond. Matter 384 (2006) 224.
[4] E. Restrepo-Parra, C.M. Bedoya-Hincapié, F.J. Jurado, J.C. Riano-Rojas, J. Restrepo J. Magn. Magn. Mater., In Press, Available online 3 July 2010.
[5] H. Huhtinen, R. Laiho, K. G. Lisunov, V. N. Stamov, and V. S. Zakhvalinskii, J. Magn. Magn. Mater., 238 (2002) 160-167.
[6] T. Hotta, A. Feiguin, and E. Dagotto, Phys. Rev. Lett. 86 (2001) 4922.
[7] E. Restrepo-Parra, J. Restrepo, J. F. Jurado, C. Vargas-Hernández and J. C. Riaño-Rojas, IEEE Trans. Magn. 45 (2009) 5180.
[8] J. C Riaño-Rojas, E. Restrepo-Parra, G. Orozco-Hernández, J. Restrepo, J. F. Jurado, and C. Vargas-Hernández, IEEE Trans. Magn. 45 (2009) 5196.
[9] S. Chakravarty, B.I. Halperin, D.R. Nelson, Phys. Rev. Lett. 60 (1988) 1057.
[10] W. Xue, G. S. Grest, M. H. Cohen, S. K. Sinha, C. Soukoulis, Phys. Rev., 38 (1998) 6868.
[11] P. Monceau, M. Perreau, F. Hebert, Phys. Rev. B 58 (1998) 1210.
[12] E. Dagotto, nanoscale phase separation and colossal magnetoresistence, Spring Verlag, Berlin, 2002.
[13] D. P. Landau and K. Binder, (2005), A guide to Monte Carlo simulations in statistical physics, 2nd Edition, Cambridge University Press.
[14] P.Papon, J.Leblond, P.h.E. Mejier, The Physics of Phase Transitions, second edition, Springer, Berlin (2006).
[15] K. H. Ahn, X. W. Wu, K. Liu, and C. L. Chien, J. Appl. Phys. 81 1997) 5770.
[16] Hans-Karl Janssena, Uwe C. Tauber, Annals of Physics 315 (2005) 147.
[17] A. P. Ramirez, J. Phys: Condens. Matter 9 (1997) 8171.
[18] K.H. Ahn, A.J. Millis, Physica B 312–313 (2002) 766.
[19] S Keshri, V. Dayal, , PRAMANA, J. Phys. 70 (2008) 697.
[20] T. Zhao, S. B. Ogale, S. R. Shinde, and R. Ramesh, R. Droopad, J. Yu, and K. Eisenbeiser, J. Misewich, App. Phy. Let. 84 (2004) 750.
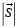 =3/2), que se enlazan con los iones A2+, Mn3+eg y Mn3+eg' (espín
=3/2), que se enlazan con los iones A2+, Mn3+eg y Mn3+eg' (espín 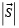 =2) que se relacionan con los iones Re3+. Estos materiales tienen estructura tipo perovskita (red cúbica simple) para el caso ideal con un número de coordinación de seis [5]. En la literatura existen muchas simulaciones teóricas que emplean diferentes métodos como dinámica molecular, cálculos ab-initio y Monte Carlo [6]. Para el caso de la simulación presentada en este trabajo se empleó una organización periódica de iones como la propuesta por Hotta et al. [6]. El modelo empleado se basa en un hamiltoniano tridimensional clásico de Heinsenberg dentro de la primera coordinación magnética. Los iones magnéticos Mn3+eg', Mn3+eg and Mn4+d3 se representan por espines clásicos de Heinsenberg, mientras que el oxígeno, y los iones Re y A se consideran no magnéticos. Los espines interactúan vía parámetros de intercambio dependiendo de la valencia. El hamiltoniano usado en este trabajo está dado por [7]:
=2) que se relacionan con los iones Re3+. Estos materiales tienen estructura tipo perovskita (red cúbica simple) para el caso ideal con un número de coordinación de seis [5]. En la literatura existen muchas simulaciones teóricas que emplean diferentes métodos como dinámica molecular, cálculos ab-initio y Monte Carlo [6]. Para el caso de la simulación presentada en este trabajo se empleó una organización periódica de iones como la propuesta por Hotta et al. [6]. El modelo empleado se basa en un hamiltoniano tridimensional clásico de Heinsenberg dentro de la primera coordinación magnética. Los iones magnéticos Mn3+eg', Mn3+eg and Mn4+d3 se representan por espines clásicos de Heinsenberg, mientras que el oxígeno, y los iones Re y A se consideran no magnéticos. Los espines interactúan vía parámetros de intercambio dependiendo de la valencia. El hamiltoniano usado en este trabajo está dado por [7]: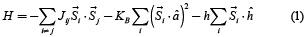
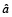 indica la dirección del eje fácil. El tercer término presenta la influencia del campo magnético externo, siendo
indica la dirección del eje fácil. El tercer término presenta la influencia del campo magnético externo, siendo 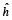 la dirección en la que se aplica dicho campo. Se consideran tres tipos de iones: Mn3+eg'-O- Mn3+eg, Mn3+eg-O-Mn4+d3 y Mn3+ eg'-O-Mn4+d3 con parámetros de intercambio Jab, Jab1 y Jab2. Estos parámetros dependen del tipo de manganita que se desea simular; por ejemplo, para el caso de La2/3Ca1/3MnO3, E. Restrepo et al. [8] reportaron simulaciones de este material al emplear el modelo de Heisenberg, y reproducir la temperatura de Curie Tc (260 K). Los valores numéricos empleados para estos parámetros fueron Jab=4.65 meV, Jab1=7.7 meV y Jab2=1.35 meV. En este caso se empleó el algoritmo de Metrópolis con el fin de obtener las propiedades de equilibrio [3]. Este modelo entonces incluye características propias del material como son el ordenamiento orbital y la mezcla de espines tipo Heisenberg. Por otro lado, aunque la energía elástica es usualmente mayor que la magnética, tal contribución hace parte de un valor constante dentro de la energía interna sin presentar cambios; por lo tanto, los iones se consideran en posiciones fijas, se desprecia la contribución de energía elástica, y se tiene un hamiltoniano puramente magnético.
la dirección en la que se aplica dicho campo. Se consideran tres tipos de iones: Mn3+eg'-O- Mn3+eg, Mn3+eg-O-Mn4+d3 y Mn3+ eg'-O-Mn4+d3 con parámetros de intercambio Jab, Jab1 y Jab2. Estos parámetros dependen del tipo de manganita que se desea simular; por ejemplo, para el caso de La2/3Ca1/3MnO3, E. Restrepo et al. [8] reportaron simulaciones de este material al emplear el modelo de Heisenberg, y reproducir la temperatura de Curie Tc (260 K). Los valores numéricos empleados para estos parámetros fueron Jab=4.65 meV, Jab1=7.7 meV y Jab2=1.35 meV. En este caso se empleó el algoritmo de Metrópolis con el fin de obtener las propiedades de equilibrio [3]. Este modelo entonces incluye características propias del material como son el ordenamiento orbital y la mezcla de espines tipo Heisenberg. Por otro lado, aunque la energía elástica es usualmente mayor que la magnética, tal contribución hace parte de un valor constante dentro de la energía interna sin presentar cambios; por lo tanto, los iones se consideran en posiciones fijas, se desprecia la contribución de energía elástica, y se tiene un hamiltoniano puramente magnético.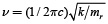 , siendo c la velocidad de la luz, k la constante de fuerza del enlace y mr = m1m2/(m1 + m2) la masa reducida que depende de los dos iones del enlace, que en este caso son el manganeso y el oxígeno (teniendo en cuenta que se tienen estructuras Mn-O-Mn). Debido a que el oxígeno es muy pequeño, la frecuencia de vibración es alta y, por ende, el desplazamiento (que es inversamente proporcional a la frecuencia) es pequeño, lo que permite eliminar cualquier influencia del desorden dinámico o térmico sobre las constantes de intercambio [10].
, siendo c la velocidad de la luz, k la constante de fuerza del enlace y mr = m1m2/(m1 + m2) la masa reducida que depende de los dos iones del enlace, que en este caso son el manganeso y el oxígeno (teniendo en cuenta que se tienen estructuras Mn-O-Mn). Debido a que el oxígeno es muy pequeño, la frecuencia de vibración es alta y, por ende, el desplazamiento (que es inversamente proporcional a la frecuencia) es pequeño, lo que permite eliminar cualquier influencia del desorden dinámico o térmico sobre las constantes de intercambio [10].
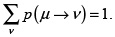 Esta probabilidad debe llenar dos condiciones: (i) no debe variar a través del tiempo y (ii) debe depender solo de las propiedades de los estados µ y v, y de ningún otro. El sistema eventualmente debe converger hacia una secuencia de estados por una probabilidad con distribución de Boltzmann que se dirige hacia el equilibrio de estados. Con el fin de alcanzar este objetivo se deben considerar dos condiciones: (i) la ergodicidad del sistema y (ii) el balance detallado. Para mayor información ver la referencia [13] y las referencias dentro de ella.
Esta probabilidad debe llenar dos condiciones: (i) no debe variar a través del tiempo y (ii) debe depender solo de las propiedades de los estados µ y v, y de ningún otro. El sistema eventualmente debe converger hacia una secuencia de estados por una probabilidad con distribución de Boltzmann que se dirige hacia el equilibrio de estados. Con el fin de alcanzar este objetivo se deben considerar dos condiciones: (i) la ergodicidad del sistema y (ii) el balance detallado. Para mayor información ver la referencia [13] y las referencias dentro de ella.
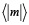 ), calor específico (Cv) y susceptibilidad (χ) [13].
), calor específico (Cv) y susceptibilidad (χ) [13].