ARTÍCULOS

CONSUMO DE COMBUSTIBLE EN VEHÍCULOS PARA TRANSPORTE POR CARRETERA –MODELOS PREDICTIVOS–

FUEL CONSUMPTION IN VEHICLES FOR HIGHWAY TRANSPORTATION – PREDICTIVE MODELS

John Jairo Posada Henao^* ; Carlos A. González-Calderón^**

^* Ingeniero Civil-Especialista en Vías y Transporte – PhD en Ingeniería. Profesor Asociado, Departamento de Ingeniería Civil, Facultad de Minas, Universidad Nacional de Colombia-Sede Medellín. Carrera 80 65-223 Bloque M5, Tel: 4+4255183, Fax: 4+4255152, jjposada@unal.edu.co

^** Ingeniero Civil, Magíster en Ingeniería – Infraestructura y Sistemas de Transporte, Master of Engineering – Transportation. Profesor 200 Años Universidad de Antioquia. Research Assistant-Center for Transportation, Infrastructure and the Environment Rensselaer Polytechnic Institute. 110 8th Street, Room JEC 4037, Troy, NY 12180 USA. Phone: +1 518-276-3121. Fax: +1 518-276-48331. gonzac4@rpi.edu

Recibido: 22/10/2012
Aceptado: 25/10/2013

RESUMEN

En este artículo se presentan modelos para la estimación del consumo de combustible en vehículos para transporte por carretera, con base en literatura especializada del tema y de costos de operación vehicular en los cuales está inmerso el combustible necesario para la locomoción de los vehículos. El consumo de combustible está asociado a variables como las características del vehículo, carga transportada y carretera por la que se circula, por lo que se considera dentro de la estructura de costos de operación vehicular como una componente variable, representando entre el 20 % y 60 % de estos costos. Para su cuantificación existen métodos directos e indirectos que han permitido la creación de algunos modelos que predicen, con cierto grado de exactitud, el consumo para condiciones particulares de operación de los vehículos, los cuales deben ser adaptados a las condiciones particulares de cada lugar.

PALABRAS CLAVE

consumo de combustible, costo de operación vehicular, modelos de predicción, evaluación de proyectos.

ABSTRACT

This article deploys models intended for estimating fuel consumption in vehicles for highway transportation, based on literature specialized in this topic and vehicle operation costs which include the fuel needed for reaching vehicle locomotion. Fuel consumption has been associated to variables such as vehicle characteristics, transported load, and circulation highway, so fuel consumption is deemed as a variable component within the vehicle operation costs structure, accounting for 20% and 60% of such costs. For its quantification, there are direct and indirect methods which can be used which allow creating some prediction models which, with a certain degree of accuracy, may predict consumption for specific operation conditions of vehicles which should be adjusted to certain conditions of each site.

KEY WORDS

Fuel consumption; vehicle operation costs; prediction models; project evaluation.

INTRODUCCIÓN

Al considerar el ciclo de vida de una carretera, los costos de operación vehicular son el componente más significativo del costo total. El consumo de combustible es el mayor componente en estos costos de operación vehicular [1]; de otro lado en la mayoría de los países el transporte por carretera es el principal modo de transporte [2].

El consumo de combustible es un importante elemento dentro del costo de operación de un vehículo que puede incluso, para algunos tipos de vehículos en algunas regiones, representar hasta el 50 % de los costos de transporte por unidad vehicular [3-6].

Desde que se inventó el vehículo, se han realizado numerosas investigaciones [7-36] tendentes a conocer el consumo de combustible utilizado para su locomoción y mejor, aún, a predecirlo. Como ejemplo, Agg [7] investigó el consumo de combustible y Moyer y Winfrey [8] fueron los primeros en realizar encuestas y estudios de costos operacionales en vehículos. Recientemente estos estudios se han orientado a conocer el efecto que en el consumo de combustible tienen aspectos como velocidad, geometría vial y estado del pavimento, entre otros.

Inicialmente los investigadores usaron datos empíricos gruesos que posteriormente se han remplazado por resultados de estudios experimentales en los cuales se ha relacionado el consumo de combustible con las condiciones específicas de operación y modelación usando una aproximación empírica. En las últimas épocas se ha modelado el consumo de combustible usando principios mecanicistas que lo relacionan con las fuerzas de oposición al movimiento [1].

Para calcular el consumo de combustible se recurre a modelos de estimación estadística o mecanicista; los primeros son económicos y sencillos de construir, y los segundos requieren gran cantidad de recursos para su desarrollo y formulación [4]. Lo actual de estos modelos es que sean de tipo mecanicista y se consideran parte integral de otros cuyo objeto es apoyar la evaluación técnica y económica de proyectos viales.

1. LOS MODELOS

Los modelos de evaluación técnico-económica han surgido para hacer más ágil, eficiente y segura la distribución de los recursos en el área vial, debido a la situación que se origina a partir de que los recursos asignados ese sector son cada vez más escasos, las carreteras se van envejeciendo y el tránsito en volumen y carga, que los solicita y deteriora, aumenta cada vez más. Estos modelos determinan la alternativa óptima de inversión, entre alternativas de diseño, construcción y mantenimiento que se consideren, utilizando el principio de minimización del costo total del transporte, concepto que ha ganado consenso entre administradores, economistas e ingenieros en los países desarrollados y economías emergentes [37].

La metodología de estos modelos contempla la interacción entre los componentes del costo de transporte (estudios y diseños, construcción, operación, mantenimiento, expansión, y de los usuarios de los vehículos), para obtener el menor costo total. Estos costos no son independientes, tienen una relación que es determinante al calcularlos.

El costo de los usuarios se compone por los de operación de los vehículos (VOC, por sus siglas en Inglés) y del tiempo de viaje, seguridad y accidentes, y comodidad. Al seleccionar la mejor alternativa de inversión, los costos de los usuarios son cerca del 90 % del costo total de transporte en carreteras de dos carriles con pocos miles de vehículos diarios [38].

El costo de operación de los vehículos es el asociado con la propiedad, operación y mantenimiento del vehículo, e incluye el costo por consumo de combustible y lubricantes, desgaste de neumáticos, repuestos, mano de obra en mantenimiento, depreciación e interés, licencias, seguros y salario de la tripulación, entre otros.

Los modelos VOC se basan en que el consumo de recursos y la velocidad de los vehículos dependen de características de los vehículos y de variables relativas al diseño, construcción y mantenimiento de la carretera, que pueden controlarse según las decisiones de inversión tales como pendiente, curvatura, peralte y rugosidad, entre otras. El objetivo de estos modelos VOC es simular los efectos de las características físicas y la condición de la carretera sobre el consumo de recursos de los vehículos. Al considerar las características de carretera, antes y después de alguna intervención, se puede con los modelos VOC determinar el costo total de usuario asociado a cada opción y luego comparándolos se obtienen los beneficios logrados por la intervención prevista.

Entre los beneficios más importantes obtenidos por las mejoras realizadas en un sistema carretero está la reducción en el consumo de combustible con el uso de modelos precisos y sencillos, para su determinación; sobre todo cuando se requiere diseñar y evaluar acciones de administración de carreteras y específicamente de pavimentos [3, 4]. De esta manera surgen los modelos para la determinación en forma predictiva del consumo de combustible en los vehículos automotores.

El consumo de combustible es influenciado por la geometría y condición de la carretera, por las condiciones de circulación y el tipo de vehículo [39], y también por las características del conductor y del ambiente en el cual se encuentra inmerso [6].

Para predecir el consumo de combustible se recurre a modelos de estimación estadística o empíricos, y los mecanicistas [4]. Los de estimación estadística, que han sido los más usados, surgen de relacionar, mediante técnicas como la regresión, el consumo, con las características geométricas y estado de una carretera; su obtención es económica y sencilla, y su limitación o problema está en la elección y uso de la técnica de regresión. Los modelos mecanicistas se fundamentan en tener en cuenta las fuerzas que están involucradas en el movimiento de los vehículos, considerando así la energía necesaria para lograr el movimiento; estos modelos están libres de muchas limitaciones y se pueden adaptar más fácilmente a entornos diferentes a aquel en el cual fueron creadas.

Es necesario calibrar cualquier modelo cuando su aplicación es en condición diferente al de su elaboración, ya que aspectos como las condiciones particulares de estudio, desactualización o alcance alteran, y seriamente en algunos casos, el proceso de elección de alternativa produciendo resultados alejados de la realidad. Los modelos de costo de operación vehicular poseen, entre otros, aspectos relacionados con la región en la que fueron desarrollados, tecnología del vehículo, comportamiento del conductor y decisiones del operador de flota, por lo que no escapan de tener que ser calibrados [3].

A continuación se describen algunos de los modelos más conocidos para estimar el consumo de combustible de vehículos que utilizan combustible tipo gasolina o aceite combustible para motores (ACPM) para su locomoción.

1.1 Modelos empíricos

También conocidos como clásicos o de estimación estadística. Una aproximación a los modelos para costos de operación vehicular considera para cada componente, como el combustible, las características de la carretera con análisis de datos por la técnica de los mínimos cuadrados teniendo un término de error [3], como se muestra en la ecuación (1).

Donde:

c = costo o consumo del elemento

x = vector de características de la carretera

f = vector de coeficientes

e = error.

El error ''e'' no puede estar correlacionado con ''x'', usualmente ''f'' se determina por mínimos cuadrados, y es posible que ''c'' se remplace por log(c) con el fin de facilitar la obtención de resultados de manera lineal, por lo que el modelo será semilogarítmico, y puede presentar un mejor ajuste.

Otros estudios plantean que el consumo de combustible es función solo de la velocidad del vehículo [3], y se establece la relación funcional que se muestra con la ecuación (2):

Donde:

F = consumo de combustible por unidad de distancia

a, b y c = coeficientes

V = velocidad del vehículo

El consumo de combustible tiene comportamiento de curva en ''U'' [40], como se muestra en la figura 1, en el que el mayor consumo de combustible se presenta a velocidades relativamente altas o bajas, y un valor mínimo cuando la velocidad del vehículo es igual a (b/2c)^1/3 [3]; o bien una denominada velocidad ''óptima'', generalmente entre 40 y 60km/h, con el mínimo de consumo [1]. El coeficiente ''a'' es función de características de la carretera y del vehículo en las cuales tienen participación el peso y la relación peso/potencia del vehículo [3]. Se muestra en la ecuación (3) otra expresión obtenida con pruebas de laboratorio [41].

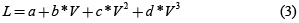
Donde:

L = consumo en lt/km

V = velocidad media en km/h

a, b, c y d son parámetros definidos para cada tipo de vehículo

Con (3) se tiene comportamiento del consumo de combustible similar al que se ilustra en la figura 1, es decir, en forma de ''U''; aunque no es muy adecuado debido a que sus resultados no se han validado con datos reales de vehículos en operación.

Un avance en el desarrollo de estos modelos se evidencia con la ecuación (4) [1, 40] que igualmente muestra, como la figura 1, que el consumo de combustible es en forma de ''U''. El avance citado corresponde a que se considera en forma explícita la pendiente de la carretera y el estado superficial del pavimento, como variables significativas.

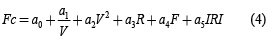
Donde:

Fc: consumo de combustible (lt/1000km)

V: velocidad del vehículo (km/h)

R: promedio de subidas de la carretera (m/km)

F: promedio de bajadas de la carretera (m/km)

IRI: rugosidad en la escala del IRI-Índice de Regularidad Internacional-(m/km)

ai: parámetros del modelo

Los modelos estadísticos clásicos, los más utilizados, han surgido de bases de datos obtenidas con encuestas, consultas a transportadores y trabajos experimentales en los que se relacionan el consumo de combustible con las características geométricas y de estado de la carretera mediante técnicas de regresión lineal múltiple. Son económicos y sencillos de construir, no involucran gran cantidad de variables, pero requieren buena base de datos. Por lo general son estadísticamente significativos y conceptualmente válidos.

Las limitaciones más comunes de estos modelos están asociadas a la técnica de regresión; por ejemplo, la aplicación de un modelo estadístico es válida solo para el vehículo considerado en la modelación, rango de variables analizado, y región donde fue desarrollado, no siendo posible utilizarlo para condiciones diferentes (los resultados no se pueden extrapolar). Esta limitación se acentúa si se desean introducir cambios por avances tecnológicos, o remplazar alguno de sus componentes, por lo que se debe realizar una nueva modelación [4].

1.2 Modelos mecanicistas

Los modelos mecanicistas, modernos para estimar el consumo de combustible de los vehículos, emplean principios que relacionan el consumo de combustible con las fuerzas que actúan sobre el vehículo. Los más exactos son utilizados por diseñadores y fabricantes de vehículos para evaluar la sensibilidad del consumo ante cambios en componentes del motor, cuerpo del vehículo o características aerodinámicas. Estos modelos, llamados de ''mapeo del motor'', requieren datos particulares y específicos que generalmente no son públicos. Además están asociados normalmente a un tipo de vehículo lo que hace difícil su uso en el área de evaluación de proyectos o de gestión de pavimentos [4], en la que se necesita conocer el consumo de una flota vehicular.

Los modelos comunes de tipo mecanicista relacionan el consumo instantáneo de combustible (ml/s) con las fuerzas que actúan sobre el vehículo en su movimiento [42]. Para calcular el consumo de combustible se relaciona este con la energía requerida para vencer las fuerzas que se oponen al movimiento, obteniendo un modelo en función de la resistencia del aire, pendiente, curvatura, rodadura e inercia del motor y del vehículo. Estudios hechos indican que las fuerzas que se deben considerar para la determinación del consumo de combustible, y otros aspectos que deben ser tenidos en cuenta son [1, 39, 40]:

• Fuerzas de oposición al movimiento: la inercia por ejemplo

• Fuerzas internas del vehículo: la fricción interna de las partes del vehículo

• Velocidad del motor: efectos por cambio en la velocidad del motor (revoluciones)

• Apropiado cálculo del consumo por eventos de aceleración y desaceleración

• Aplicable a diferentes vehículos: diferentes tipología y tecnología

Los modelos mecanicistas no tienen limitaciones, ya que pueden considerar cambios tecnológicos y ser aplicados a otros ambientes, siendo su mayor ventaja que poseen una mayor flexibilidad de aplicación modificando el parámetro de interés sin necesidad de realizar nuevos ensayos. La principal desventaja de estos modelos es que requieren gran cantidad de recursos para su desarrollo y formulación [4].

Tres grandes estudios se han hecho para desarrollar modelos mecanicistas: el estudio auspiciado por el Banco Mundial para el Highway Design and Maintenance Standars Model (HDM-III), investigación en Sur África, y en Australia [39], en los que se usó la magnitud de las fuerzas que se oponen al movimiento como base para las predicciones.

En los estudios de Sur África y Australia se pretendió obtener un factor de eficiencia. El consumo de combustible fue el producto del total de potencia requerida para vencer fuerzas de oposición al movimiento, y este factor de eficiencia [40].

El modelo del HDM-III se ha considerado como mecanicista híbrido, ya que usa como base para sus cálculos las fuerzas que se oponen al movimiento y luego recurre al uso de una serie de parámetros de regresión para convertir dichas fuerzas en consumo de combustible. A diferencia del modelo de Sur África, Greenwood [40] explica que este explícitamente considera la velocidad del motor, aunque adopta un valor constante.

Otros modelos son:

Australian Road Fuel Consumption Model (ARFCOM) es un modelo mecanicista cuya ventaja es que permite conocer el consumo de combustible en ralentí (motor funcionando pero caja de velocidades en neutro) [39].

El International Study of Highway Development and Management –ISOHDM– se realizó para ampliar el ámbito del HDM-III y armonizar los sistemas de gestión de carreteras con software adaptable a las necesidades de los administradores de carreteras [43]; el principal resultado es la Herramienta para Desarrollo y Gestión de Carreteras (Highway Development and Management Tool) –HDM-4–, con el que el ámbito de aplicación del sistema HDM se ha ampliado pues supera las evaluaciones tradicionales de proyectos, y proporciona un potente sistema para el análisis de gestión y de alternativas de inversión en carreteras; su uso inició en el año 2000.

A continuación se presentan los modelos más representativos destacando su importancia, como los de HDM-III y HDM-4 por ser considerados los mejores y por el apoyo y casi exigencia que hace el Banco Mundial para que los proyectos carreteros sean evaluados con estos modelos [44]. Por ejemplo Zaabar y Chatti [22] calibraron el modelo HDM-4 para estimar el efecto de la rugosidad del pavimento en el consumo de combustible para las condiciones de USA.

1.2.1 Modelo del HDM-III

Este modelo emplea un principio básico de los motores de combustión interna: bajo condiciones ambientales ideales como temperatura ambiente, presión y humedad constantes, el consumo de combustible por unidad de tiempo se puede expresar como función de la potencia de salida y las revoluciones del motor [38], con la ecuación (5):

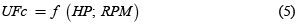
Donde:

UFc: consumo instantáneo de combustible (ml/s)

HP: potencia aplicada en las ruedas (HP)

RPM: velocidad del motor en revoluciones (rpm)

Los datos para determinar la función de consumo de combustible del modelo HDM-III se obtuvieron experimentalmente para 11 vehículos. El ensayo consideró observar el consumo en ambos sentidos sobre tramos de longitud definida con pendiente constante y diferentes niveles de carga, manteniendo constante la velocidad de viaje y la posición de la caja de cambios. Las pruebas se realizaron a velocidades de 10 a 120km/h, con incrementos de 10km/h. En cada observación se registra la cantidad de combustible que se consume y el tiempo empleado en recorrer el tramo de carretera utilizado.

El consumo de combustible instantáneo o unitario (UFc) se calcula como la cantidad de combustible que se consume en el tramo dividido entre el tiempo de viaje. Se hacen varias réplicas para cada combinación de vehículo, nivel de carga, sección, dirección, velocidad de viaje y posición en la caja de velocidades. El promedio de las observaciones para cada conjunto de combinaciones se trata como una observación individual en el análisis estadístico. La estimación de los coeficientes de la ecuación se realiza a partir de regresiones ordinarias de mínimos cuadrados, aplicada en forma separada para tramos en subida y en bajada, empleando diferentes modelos [38].

La función estimada UFc es continua en HP y RPM. Para RPM fijo el consumo UFc aumenta con HP, así si el vehículo necesita mayor potencia el consumo de combustible aumenta. De la misma forma el consumo aumenta con las revoluciones del motor para valores fijos de la potencia aplicada. Cuando la potencia aplicada es nula, HP = 0, se tiene consumo mínimo en función de RPM, que se aproxima al consumo en ralentí.

Finalmente, el consumo de combustible promedio, para un viaje en ida y vuelta o ''round trip'', está dado por la ecuación (6).

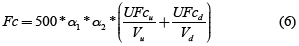
Donde:

Fc: consumo de combustible (litros por cada 1.000 km)

α₁: parámetro de ajuste por eficiencia del motor

α₂: parámetro de ajuste por forma de operación

V_u: velocidad en tramos ascendentes (m/s)

V_d: velocidad en tramos descendentes (m/s)

UFc_u: consumo de combustible instantáneo en tramos ascendentes (ml/s)

UFc_d: consumo de combustible instantáneo en tramos descendentes (ml/s)

Una de las falencias del modelo de consumo del HDM III es la alta estimación para automóviles grandes y medianos, por lo que se sugiere una reducción del factor []1 para estos vehículos con el fin de tener una estimación más realista [45]. Otro aspecto está relacionado con las revoluciones del motor; se estima el consumo con la velocidad nominal del motor (CRPM) constante, equivalente a 75 % de la tasa de potencia máxima (máxRPM) del vehículo correspondiente, en vez de la real del motor.

1.2.2 Modelo del HDM-4

En el HDM-4 se tiene el modelo ARFCOM que se citó previamente. El HDM-4 es un modelo para la gestión de infraestructura vial que permite realizar evaluaciones técnicas y económicas para proyectos de inversión en carreteras [44].

Los resultados obtenidos con este modelo permiten verlo como el que mejor ajuste tiene con datos reales, y por consiguiente, es el más confiable para predicciones de consumo de combustible para condiciones de flujo de tránsito ininterrumpido [46]. En este, el consumo de combustible se predice en forma proporcional a los requerimientos de potencia que tenga el vehículo [40]. Su expresión genérica es la ecuación (7).

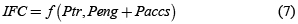
Donde:

IFC: Consumo de combustible instantáneo (ml/s)

Ptr: potencia requerida por fuerzas tractivas (kW)

Paccs: potencia requerida por accesorios (kW)

Peng: potencia requerida por fricción interna del motor (kW)

Para estimar el consumo de combustible, el modelo calcula primero la suma de los componentes de potencia externa (potencia tractiva, incluyendo la eficiencia del tren de tracción, y la potencia de accesorios) y la potencia para sobreponerse a la fricción interna del motor [4]. Luego, de acuerdo con la ecuación (8) el consumo instantáneo de combustible se estima usando el factor de eficiencia consumo-potencia, así:

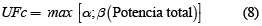
Donde:

UFc: consumo de combustible instantáneo (ml/s)

α: consumo de combustible mínimo, usualmente el de ralentí (ml/s)

β: factor de eficiencia consumo de combustible-potencia (ml/kw/s)

Potencia Total: la requerida para vencer las resistencias externas: rodadura, inercia, aerodinámica, curvatura y pendiente (Potencia tractiva: Ptr), mover los accesorios del vehículo (Potencia de accesorios: Paccs), y vencer la fricción interna del motor (Peng).

El modelo considera que el consumo de combustible para una potencia total reducida no será inferior a la tasa de ralentí (α), que es el mínimo combustible requerido para mantener el motor en funcionamiento sin presionar el acelerador y caja de velocidades en neutro. Este consumo incluye el combustible necesario para vencer la fricción interna del motor y mover los accesorios con el vehículo detenido. Si esta tasa en ralentí es desconocida, el modelo original permite determinarla; igual sucede con el resto del modelo HDM-4 que proporciona valores por defecto para otras muchas variables [44].

En condiciones generales de conducción, el consumo de combustible continuamente varía debido a los cambios permanentes en la velocidad del vehículo y las condiciones de la carretera. En niveles bajos de aceleración el consumo de combustible toma un valor mínimo que depende de la tecnología del motor. Motores con control computarizado de inyección de combustible y algunos carburados de los más recientes, tienen la capacidad de restringir el consumo de combustible a un nivel muy bajo (conocido como combustible cero), incluso menor al de ''ralentí'' durante períodos en donde la potencia tractiva es suficiente para atender requisitos por accesorios y fricción interna del motor. Esto es relevante en casos de altas pendientes longitudinales de la carretera, o niveles de congestión en los que es alta la cantidad de maniobras [40].

Este modelo es el mejor según varios investigadores [1, 4, 40, 46]. Y aunque su descripción puede ser consultada en Odoki y Kerali [47], también está disponible con mayor detalle en Posada [48] donde incluso se presenta corrección a una de las fórmulas del modelo. Sin embargo, luego de revisiones al software correspondiente se detecta que fue un error tipográfico en los respectivos manuales.

1.2.3 Modelo COPER

Este es un modelo de costos de operación vehicular desarrollado en Chile [4], pero no es un modelo original, ya que realmente es una calibración del modelo del HDM-III. En Chile se estimó conveniente adaptar algún modelo existente de consumo de combustible en lugar de desarrollar uno nuevo, debido al alto costo que implica. La selección comenzó con el análisis de diversos modelos disponibles en el momento (1990), de tal manera que por su formulación teórica, se pudiera adaptar a condiciones locales. Se recomendó utilizar la formulación del HDM-III, por los siguientes aspectos:

• Permite incluir explícitamente características de vehículos (masa, área frontal, etc.).

• Aumenta el rango de validez de funciones para variables geométricas y de rugosidad.

• Incorpora los efectos de la tecnología automotriz en el rendimiento de los vehículos.

• Permite validaciones con experimentos por su concepción físico-experimental.

La modificación de los parámetros que establece la regresión para el HDM-III permitió ajustar el modelo a condiciones locales. No obstante, se aconsejó la realización de pruebas de consumo de combustible para asegurar la bondad del modelo. Los camiones pequeños y buses presentaron mejor ajuste que los automóviles y camionetas, pero para camiones medianos y pesados las diferencias fueron mayores.

2. NECESIDAD DE ADAPTACIÓN Y CALIBRACIÓN

Varios estudios que fundamentan los modelos existentes se realizaron con vehículos de la década de 1980 [4, 49], por lo que se resta actualidad y precisión al modelo debido a los avances en la tecnología de los vehículos durante el tiempo transcurrido desde que dichos estudios se realizaron. Además, varios de ellos se han hecho con vehículos nuevos del momento [3], situación que influye en el rendimiento del vehículo hasta que todas sus piezas se acoplen y el funcionamiento del vehículo se estabilice.

Las características de los modelos hacen imprescindible, por las condiciones normales bajo las cuales son creados, que sean adaptados a las condiciones del lugar donde se utilizarán para lo cual es necesario realizar investigaciones que permitan efectuar en forma adecuada tal adaptación y así los resultados obtenidos sean fiables [48]; situación que no es ajena a la realidad de muchos lugares como Colombia, en donde no se han realizado trabajos de este tipo [50]. Esto se estima de alta conveniencia para poder conocer con mayor precisión el efecto de las intervenciones en las carreteras.

Algunos estudios se han hecho para adaptar y calibrar estos modelos a condiciones locales de uso [42]. Se ha encontrado en estos estudios que existen diferencias, entre los datos del modelo y los reales, cercanas al 200 % [46]; y en particular para el caso del HDM-4 se presenta un rango entre 110 % y 270 %, para camiones [48].

3. CONCLUSIONES

La correcta estimación del consumo de combustible es indispensable en la evaluación de proyectos viales, debido a la importancia que este tiene dentro de los costos de usuario que son vitales en dicho proceso de evaluación.

Los modelos para el cálculo del consumo de combustible son de dos tipos básicamente: empíricos, clásicos o de estimación estadística, y los de tipo mecanicista. Estos últimos son más versátiles y permiten una mejor adaptación a condiciones locales o particulares de estudio, pero para su desarrollo y formulación se requieren muchos recursos. Los modelos mecanicistas se identifican como mejores que los empíricos, ya que permiten modelar el consumo acorde con características del vehículo y de factores que tienen influencia en las fuerzas que se oponen al movimiento.

Los modelos para la estimación del consumo de combustible deben ser analizados con cuidado para adaptarlos y calibrarlos a las condiciones locales de uso, de tal manera que los resultados obtenidos sean válidos para los fines propuestos en los estudios, como es el caso de evaluación de proyectos viales.

El modelo de mayor validez que se tiene actualmente es el que se encuentra inmerso en el HDM-4, de amplio uso en el ámbito internacional.

REFERENCIAS

[1] I. D. Greenwood and C. R. Bennett, HDM-4 Fuel Consumption Modelling. Birmingham: University of Birmingham, 1995.

[2] I. Sarmiento and M. Franco, ''El transporte de mercancías por carretera, un elemento esencial en la economía colombiana,'' in V Congreso de ingeniería de transporte – CIT Santander, 2002.

[3] A. Chesher and R. Harrison, ''Vehicle operating costs: evidence from developing countries,'' International Bank for Reconstruction and Development, Washington, DC (USA) PB-88-208574/XAB, 1987.

[4] A. L. Altamira, ''Determinación del consumo de combustible de vehículos pesados sobre distintos tipos de pavimento,'' Doctorado, Pontificia Universidad Católica de Chile, Santiago de Chile, 2003.

[5] J. Cañadas Salas, ''Costes de operación del tráfico en la carretera'', Tesina, Universidad Politécnica de Cataluña, Barcelona, 2007.

[6] J. A. Arroyo Osorno and R. Aguerrebere Salido, ''Estado superficial y costos de operación en carreteras,'' Instituto Mexicano de Transporte, Sanfandila2002.

[7] T. R. Agg, ''The Economics of Highway Grades,'' Ames, Iowa 1923.

[8] R. A. Moyer and R. Winfrey, ''Cost of Operating Rural Mail Carrier Motor Vehicles on Pavement, Gravel and Earth,'' 1939.

[9] R. Harrison, ''Influence of road-surface roughness on Vehicle Operating Costs: reviewing the evidence from developing countries,'' in Surface characteristics of roadways: international research and technologies, 1990, pp. 416-429.

[10] R. Bonney and N. F. Stevens, ''Vehicle Operating Costs on Bituminous, Gravel and Earth Roads in East and Central Africa,'' Road Research Lab Tech Papers/UK/, 1967.

[11] H. W. Du Plessis, A. T. Visser, and P. C. Curtayne, ''Fuel consumption of vehicles as affected by road-surface characteristics,'' Surface characteristics of roadways: International research and technologies, ASTM STP, vol. 1301, pp. 480-496, 1990.

[12] J. P. Zaniewski and B. C. Butler, ''Vehicle operating costs related to operating mode, road design, and pavement condition,'' ASTM Special Technical Publication, vol. 884, pp. 127-142, 1985.

[13] J. P. Zaniewski, B. Butler, G. Cunningham, G. Elkins, and M. Paggi, ''Vehicle operating costs, fuel consumption, and pavement type and condition factors,'' 1982.

[14] I. De Vlieger, ''On board emission and fuel consumption measurement campaign on petrol-driven passenger cars,'' Atmospheric Environment, vol. 31, pp. 3753-3761, 1997.

[15] M. Ross, ''Automobile fuel consumption and emissions: Effects of vehicle and driving characteristics,'' Annual Review of Energy and the Environment, vol. 19, pp. 75-112, 1994.

[16] A. Cappiello, I. Chabini, E. K. Nam, A. Lue, and M. Abou Zeid, ''A statistical model of vehicle emissions and fuel consumption,'' in Intelligent Transportation Systems, 2002. Proceedings. The IEEE 5th International Conference on, 2002, pp. 801-809.

[17] J. Van Mierlo, G. Maggetto, E. Van de Burgwal, and R. Gense, ''Driving style and traffic measures-influence on vehicle emissions and fuel consumption,'' Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, vol. 218, pp. 43-50, 2004.

[18] R. Akçelik and M. Besley, ''Operating cost, fuel consumption, and emission models in aaSIDRA and aaMOTION,'' in 25^th Conference of Australian Institutes of Transport Research (CAITR 2003), University of South Australia, Adelaide, Australia, 2003, pp. 3-5.

[19] R. Akçelik and D. Biggs, ''Acceleration profile models for vehicles in road traffic,'' Transportation Science, vol. 21, pp. 36-54, 1987.

[20] R. Akçelik and M. Besley, ''Acceleration and deceleration models,'' in 23^rd Conference of Australian Institutes of Transport Research (CAITR 2001), Monash University, Melbourne, Australia, 2001, pp. 10-12.

[21] H. Rakha and Y. Ding, ''Impact of stops on vehicle fuel consumption and emissions,'' Journal of Transportation Engineering, vol. 129, pp. 23-32, 2002.

[22] I. Zaabar and K. Chatti, ''Calibration of HDM-4 models for estimating the effect of pavement roughness on fuel consumption for US conditions,'' Transportation Research Record: Journal of the Transportation Research Board, vol. 2155, pp. 105-116, 2010.

[23] E. Pelensky, W. Blunden, R. Munro, W. SAGGERS, N. D. Clark, T. Soloman, and N. Fisher, ''Operating costs of cars in urban areas,'' in Australian Road Research Board Conference Proc, 1968.

[24] L. Ferreira, ''Estimating Vehicle Fuel Consumption in Urban Areas,'' 1981.

[25] S. Ardekani, E. Hauer, and B. Jamei, ''Traffic impact models,'' Chapter 7 in Traffic Flow Theory, Oak Bridge National Laboratory Report, 1992.

[26] L. Evans, R. Herman, and T. Lam, ''Multivariate analysis of traffic factors related to fuel consumption in urban driving,'' Transportation Science, vol. 10, pp. 205-215, 1976.

[27] K. Post, J. Kent, J. Tomlin, and N. Carruthers, ''Fuel consumption and emission modelling by power demand and a comparison with other models,'' Transportation Research Part A: General, vol. 18, pp. 191-213, 1984.

[28] G. Song, L. Yu, and Z. Wang, ''Aggregate fuel consumption model of light-duty vehicles for evaluating effectiveness of traffic management strategies on fuels,'' Journal of Transportation Engineering, vol. 135, pp. 611-618, 2009.

[29] D. J. Graham and S. Glaister, ''The demand for automobile fuel: a survey of elasticities,'' Journal of Transport Economics and Policy (JTEP), vol. 36, pp. 1-25, 2002.

[30] K. A. Small and E. T. Verhoef, The Economics of Urban Transportation, 2nd ed.: Routledge, 2007.

[31] C. R. Bennett, The New Zealand Vehicle Operating Costs Model vol. 2, 1987.

[32] A. Ihs and L. Sjögren, An overview of HDM-4 and the Swedish Pavement Management System (PMS): VTI, 2003.

[33] I. D. Greenwood and C. R. Bennett, ''The effects of traffic congestion on fuel consumption,'' Road and Transport Research, vol. 5, pp. 18-35, 1996.

[34] L. Gyenes and C. Mitchell, ''The effect of vehicle-road interaction on fuel consumption,'' ASTM Special Technical Publication, vol. 1225, pp. 225-225, 1994.

[35] L. Schipper and W. Tax, ''New car test and actual fuel economy: yet another gap?,'' Transport Policy, vol. 1, pp. 257-265, 1994.

[36] H. Hide, S. Abaynayaka, I. Sayer, and R. Wyatt, ''The Kenya road transport cost study: research on vehicle operating costs,'' 1975.

[37] H. Solminihac, Gestión de infraestructura vial. Santiago de Chile: Ediciones Universidad Católica de Chile, 2001.

[38] T. Watanatada, A. M. Dhareshwar, and P. Rezende, ''Vehicle speeds and operating costs: Models for road planning and management,'' World Bank-International Bank for Reconstruction and Development, , Washington, DC. 1987.

[39] C. Bennett and I. D. Greenwood, Modelling Road User and Environmental Effects in HDM-4 vol. 7: The World Road Association (PIARC) on behalf of the ISOHDM sponsors, 2001.

[40] I. D. Greenwood, ''A new approach to estimate congestion impacts for highway evaluation: effects on fuel consumption and vehicle emissions,'' Ph.D. , University of Auckland, Auckland, 2003.

[41] ITEA, ''Values of Time and Operating Costs,'' UK Department for Transport, London, 2007.

[42] A. Altamira, H. De Solminihac, R. Harrison, and J. P. Covarrubias, ''Calibration of fuel consumption model in HDM4 model: An Application to observed consumption in Canada and Chile,'' in 84th Transportation Research Board Annual Meeting, Washington, DC., 2004.

[43] M. Pradena and J. J. Posada, ''Análisis de Inversiones en Carreteras Utilizando Software HDM-4,'' Revista de la Construcción, vol. 6, pp. 35-47, 2007.

[44] J. J. Posada, Evaluación de proyectos de inversión en carreteras con el HDM-4. Medellín: Universidad Nacional de Colombia Sede Medellín, 2006.

[45] R. Archondo-Callao and A. Faiz, Estimating vehicle operating costs. Washington, DC: World Bank 1994.

[46] I. Greenwood, R. Dunn, and R. Raine, ''Estimating the effects of traffic congestion on fuel consumption and vehicle emissions based on acceleration noise,'' Journal of Transportation Engineering, vol. 133, pp. 96-104, 2007.

[47] J. B. Odoki and H. G. R. Kerali, ''Analytical Framework and Model Descriptions,'' The World Road Association (PIARC) on behalf of the ISOHDM sponsors, 2000.

[48] J. J. Posada, ''Efecto de la cantidad de carga en el consumo de combustible en camiones'' Doctorado, Ingeniería Civil, Universidad Nacional de Colombia, Medellín, 2012.

[49] D. Biggs, ARFCOM: Models for Estimating Light to Heavy Vehicle Fuel Consumption. Vermont South: Australian Road Research Board, 1988.

[50] ACCEFYN, ''Línea base para proyectos de transporte masivo,'' Academia Colombiana de Ciencias Exactas, Físicas y Naturales, Bogotá D.C., 2003.