ARTÍCULOS
CARACTERIZACIÓN DE CARGAS DE BAILE EN UNA PLATAFORMA EXPERIMENTAL
CHARACTERIZATION OF DANCE LOADS ON AN EXPERIMENTAL PLATFORM
Diana Carolina Millán Yusti* ; Patricia Valenzuela** ; Peter Thomson***
* Ingeniera Civil, Estudiante de Maestría en Ingeniería con énfasis en ingeniería Civil, Universidad del Valle. Integrante del Grupo de Investigación en Ingeniería Sísmica, Ingeniería Eólica y Estructuras Inteligentes, G-7, Universidad del Valle, (Cali). Dirección: Calle 13 No 100-00 Ed. 350, laboratorio LINSE. Teléfono (57-2) 339 2420. Correo electrónico diana.c.millan@correounivalle.edu.co. Fax:3392086.
** Ingeniera Civil, Universidad del Valle. Integrante del Grupo de Investigación en Ingeniería Sísmica, Ingeniería Eólica y Estructuras Inteligentes, G-7, Universidad del Valle, (Cali). Dirección: Calle 13 No 100-00 Ed. 350, laboratorio LINSE. Teléfono (57-2) 339 2420. Correo electrónico patricia.valenzuela@hotmail.com. Fax:339 2086
*** Ingeniero aeroespacial, Ph.D, Profesor Titular de la Universidad del Valle, Director del Grupo de Investigación en Ingeniería Sísmica, Ingeniería Eólica y Estructuras Inteligentes, G-7, Universidad del Valle (Cali). Dirección: Calle 13 No 100-00 Ed. 350, Oficina 2001: Teléfono (57-2) 339 2086. Correo electrónico: peter.thomson@correounivalle.edu.co. Fax: 339 2086
Recibido: 20/09/2012
Aceptado: 25/10/2013
RESUMEN
La utilización de materiales ligeros y resistentes ha permitido la construcción de sistemas de entrepisos que satisfacen condiciones ideales espaciales y geométricas para albergar grandes cantidades de personas. A pesar que estas características de peso y resistencia representan una disminución de costos en la construcción, estos entrepisos tienden a ser más susceptibles a presentar problemas de vibraciones, especialmente cuando la excitación puede ser clasificada como actividad rítmica. En este artículo se presenta la caracterización de cargas producidas por personas realizando actividades de baile, a partir de mediciones en una plataforma experimental de escala real. Se identifican los factores de impacto y coeficientes de Fourier que representan la carga debida a personas que bailan, a la que es sometida la estructura. Los resultados de la presente investigación fueron obtenidos dentro de un proyecto de investigación financiado por Colciencias y la Universidad del Valle contrato .382-2009.
PALABRAS CLAVE
Coeficientes de Fourier, factores de impacto, actividades rítmicas, vibración excesiva, entrepisos flexibles.
ABSTRACT
The use of light and strong materials has allowed the construction of mezzanines which meet ideal spatial and geometric conditions to accommodate a significant number of people. Despite these weight and resistance characteristics represent decreased construction costs, these mezzanines tend to be more susceptible to vibration problems, especially when excitement can be classified as a rhythmic activity. This article shows characterization of loads produced by people performing dancing activities from measurements in a real scale experimental platform. Impact factors and Fourier's coefficients, which represent the load to which the structure is subject, caused by people dancing, are identified. Results of this research were obtained in a research project sponsored by COLCIENCIAS and Universidad del Valle according to Contract 382-2009.
KEY WORDS
Fourier's coefficients; impact factors; rhythmic activities; excessive vibration; flexible mezzanines.
INTRODUCCIÓN
La industrialización de la construcción y el desarrollo de materiales ligeros de alta resistencia han creado una tendencia hacia el uso de sistemas de entrepisos livianos, con menores razones de amortiguamiento y mayores separaciones entre elementos estructurales. Esto lleva a que las losas sean susceptibles a presentar problemas de vibraciones, que afecta sus condiciones de servicio y provocan incomodidad y sensación de inseguridad en los usuarios. El número de quejas con respecto a estas oscilaciones de piso ha aumentado en los últimos años, y restaurantes, aeropuertos, centros comerciales, salones de baile y edificios de oficinas con entrepisos ligeros han presentado el problema [1]. Lo anterior hace de las vibraciones en losas un tema de gran interés, por lo que muchas de las investigaciones realizadas han sido orientadas a determinar límites de frecuencia y aceleraciones pico, con el fin de desarrollar escalas de perceptibilidad humana que permitan determinar las condiciones de servicio de la estructura desde el punto de vista del confort [2, 3].
En los últimos años, con el avance de investigaciones sobre los efectos de la interacción humano/estructura, se han descrito los cambios modales de las estructuras debido a la influencia de las personas. También se ha trabajado en la determinación de las cargas dinámicas producidas por actividades humanas en estructuras como estadios, losas y puentes peatonales [4-6]. Autores como B. R. Ellis y T. Ji han desarrollado modelos analíticos para carga rítmica partiendo de la caracterización del salto de una persona, ya que se considera una acción de alto impacto [7]. Por otro lado, investigadores del Reino Unido han realizado estudios para la obtención de cargas de grupos incluyendo efectos de sincronización y las características dinámicas de la estructura [8]. Los sistemas de entrepiso donde se hacen actividades rítmicas tienen en común que el diseño no está controlado por los estados límite sino por criterios de servicio (deflexiones o vibraciones) [9]. Por esta razón la determinación de la carga viva constituye el parámetro más importante a tener en cuenta por el diseñador estructural debido a la magnitud y condiciones de servicio que se deben garantizar para lograr un desempeño óptimo. En este documento se presentan los resultados de la caracterización de las cargas dinámicas generadas en actividades rítmicas de baile, obtenidas en ensayos grupales en laboratorio sobre una plataforma experimental monitoreada con sensores de fuerza y aceleración, con el fin de analizar los efectos dinámicos producidos por las personas sobre sistemas de entrepiso en discotecas y gimnasios.
1. METODOLOGÍA
1.1. Cargas rítmicas
Las actividades rítmicas como el baile, los ejercicios aeróbicos, saltos, etc. son consideradas cargas dinámicas armónicas. En la figura 1 se presenta el modelo básico de una pareja bailando sobre un sistema de entrepiso, el cual es considerado como un sistema masa-resorte con amortiguamiento viscoso.
La ecuación diferencial ordinaria que gobierna este sistema es:

La mayoría de los problemas de vibraciones en los sistemas de piso incluyen cargas repetidas provocadas por las máquinas o por actividades humanas tales como el bailar, saltar o caminar. En términos simplificados una fuerza que se repite se puede representar por una combinación de fuerzas sinusoidales cuyas frecuencias, f, son múltiplos o armónicos de la frecuencia básica de la fuerza característica. La fuerza total aplicada está dada por la suma de la carga estática Wp y el coeficiente dinámico F(t) [10], como se expresa en la ecuación 2.
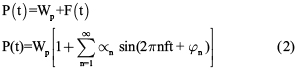
Donde:
• ∞n = Factor dinámico de carga.
• Φn = Ángulo de fase
• f = Frecuencia forzada
• Wp = Peso de los participantes
El factor de carga dinámico ∞n, está definido como el coeficiente Fourier de la fuerza dinámica de la función normalizada por el peso estático de participantes [11].
1.2. Plataforma experimental
Para cuantificar las cargas dinámicas generadas por actividades rítmicas se ejecutaron ensayos de laboratorio en una plataforma experimental de hormigón armado. Esta consiste en una losa aligerada a escala real de 4 m de ancho y 4 m de largo, con una loseta de 8 cm de espesor, soportada por vigas perimetrales de 25 cm de base por 32cm de altura y viguetas de 10 cm x 32cm. El entrepiso está apoyado sobre cuatro celdas de carga situadas en las esquinas de la losa, las cuales se ubicaron en medio de platinas de nivelación, como lo muestra la figura 2. El sistema (losa de hormigón y celdas de carga) posee una frecuencia natural superior a las frecuencias esperadas producidas por las actividades humanas, para minimizar la interacción entre la carga y la plataforma de medición.
1.3. Equipos de adquisición
En la adquisición de datos fueron usados cuatro acelerómetros sísmicos de baja frecuencia tipo Wilcoxon Research Model 731A con una sensibilidad de 10V/g. Cada uno cuenta con su acondicionador de señal WR Modelo P31 que amplificaban las señales análogas y proveían un filtro pasa-bajo con frecuencias de corte en 100 o 450 Hz. La señal fue transmitida por cables coaxiales a una caja de conexiones National Instruments CS-2345. Esta última se conectó a un computador portátil marca Dell precisión M2400 donde la señal análoga fue convertida en digital por medio de una tarjeta de adquisición DAQ Card 6024E. Para la caracterización de la fuerza se utilizaron cuatro celdas de carga Omega-Dyne LCD 401-10K que permiten obtener el registro de la carga en el tiempo, mediante señales análogas que luego de ser acondicionadas y filtradas fueron digitalizadas. Las celdas están dispuestas en las cuatro esquinas de la plataforma (figura 3) con el fin de permitir la distribución de la carga de manera uniforme.
1.4. Procesamiento de los registros de carga
Para analizar la influencia de las cargas producidas por actividades rítmicas se ejecutó una secuencia de baile sincronizado al ritmo de los géneros salsa, merengue, bachata y reggaetón. Cada rutina se ejecutó repetidas veces, incrementado de uno en uno el número de personas hasta llegar a un total de nueve individuos. Cada registro inició 80 segundos antes con la losa vacía con el fin de verificar el peso de la persona y la calibración de los equipos de adquisición. También se llevó a cabo un control visual del comportamiento de las personas durante las actividades para identificar en el análisis rangos de mayor sincronización, movimientos de alto impacto y el estado de ánimo de los participantes. Las señales fueron separadas según el género musical en diferentes intervalos para determinar las características de cada uno de los movimientos ejecutados, como se observa en la figura 4. Dichas señales se analizaron mediante un algoritmo desarrollado en el paquete matemático MATLAB, que permite obtener la transformada rápida de Fourier (FFT).
A partir de los resultados suministrados por la FFT se obtuvieron los coeficientes de Fourier para cada una de las frecuencias predominantes y sus respectivos armónicos. Además, se determinó el factor de impacto (Kp), calculado como el cociente entre la amplitud máxima de la fuerza dinámica y la fuerza estática a partir de los registros de carga. La fuerza dinámica fue calculada como el promedio de las cargas máximas producidas en el tiempo.
2. RESULTADOS
2.1. Frecuencia natural plataforma de laboratorio
La frecuencia fundamental de la plataforma se determinó a partir de registros ambientales obtenidos a una frecuencia de muestreo de 256 Hz. Cada viga y vigueta se instrumentaron con cuatro acelerómetros (figura 5). Igualmente se efectuaron ensayos de vibración forzada, utilizando un agitador de masa (shaker) con una excitación variable entre 1 Hz a 30 Hz. Dada la configuración estructural de la plataforma y la distribución de las viguetas, se encontró que la frecuencia fundamental de la losa es de 20.5 Hz correspondiente a un modo de vibración vertical. Esta frecuencia y su respectivo registro de aceleración se muestran en la figura 6.
La frecuencia modal de vibración vertical obtenida permite diferenciar la respuesta de la estructura de otro tipo de frecuencias como las producidas durante las actividades rítmicas que hacen parte de este trabajo (menores a 10 Hz).
2.2. Ensayo de baile grupal sincronizado
Se ejecutó una secuencia de baile sincronizado al ritmo de géneros como la salsa, el merengue, la bachata y el reggaetón. Cada rutina se realizó repetidas veces, aumentando de uno en uno, el número de personas hasta llegar a un total de nueve individuos.
2.2.1. Factor de impacto (Kp)
Para la obtención de los factores de impacto, la fuerza producida por las personas al bailar de manera sincronizada es normalizada por su peso estático. La tabla 1 presenta los factores de impacto obtenidos experimentalmente para cada uno de las actividades rítmicas coordinadas.
En la figura 7, se observa cómo a medida que aumenta el número de participantes, el factor de impacto tiende a disminuir, hasta tornarse constante como en el caso de la bachata. El decaimiento del valor del kp se debe a las dificultades de coordinación que se presentan en grupos de personas. Este fenómeno ha sido reportado por gran cantidad de investigaciones relacionadas con interacción humano-estructura [12, 13].
2.2.2. Coeficientes de Fourier (αn)
Con el fin de obtener la distribución de la carga dinámica generada por las actividades rítmicas, se obtuvieron los coeficientes de Fourier para cada una de las rutinas ejecutadas en forma sincronizada para los géneros de salsa, bachata, merengue y reggaetón. En la tabla 2 se presentan los valores de los coeficientes de Fourier y las frecuencias asociadas para el ritmo de salsa.
En la figura 8 se muestra la gama de frecuencias asociadas a los coeficientes de Fourier para el género de salsa, donde el armónico principal se encuentra alrededor de 1.56 Hz. A pesar de esto, el mayor aporte de carga se da en el segundo armónico, es decir en 3.19 Hz, el cual fue identificado en todos los registros. Este fenómeno se presenta porque el paso básico de salsa se ejecuta en ocho tiempos, donde el cuarto y el octavo tiempo son considerados como pausas, llevando a la persona a tener mayor contacto con la plataforma en algunos instantes, ya que durante dicho baile no se transmite el peso del cuerpo a los dos pies al mismo tiempo.
En la tabla 3, se presentan los resultados para el género bachata en la modalidad de baile sincronizado donde se puede apreciar la variación del coeficiente de Fourier y sus frecuencias asociadas, los cuales demuestran que en una frecuencia alrededor de 2.16 Hz se presenta el mayor aporte de carga.
Estos datos se muestran en la figura 9 donde se grafica la gama de frecuencias asociadas a los coeficientes de Fourier para la bachata. Se puede observar una frecuencia marcada alrededor de 2.16 Hz, la cual corresponde a los tres primeros tiempos del paso básico donde se realiza el mayor impacto.
Asímismo, se puede observar la presencia de una frecuencia marcada en 1.094 Hz, donde se genera un aporte de fuerza menor, debido a que en la ejecución en dicho tiempo se da un leve toque del pie sin llegar a pasar el peso. La variación del coeficiente de Fourier para el género de merengue y sus frecuencias asociadas se muestran en la tabla 4.
En la figura 10, se muestra la gama de frecuencias asociadas a los coeficientes de Fourier para merengue. En esta figura se pueden observar las amplitudes del armónico principal en 2.5 Hz, con un coeficiente de Fourier máximo de αmáx=0.86, con sus respectivos armónicos. Esta frecuencia da el mayor aporte de carga, ya que el merengue se caracteriza por sostener un paso básico que se combina al ejecutarlo en diferentes direcciones. Cabe resaltar que existen unos cambios de frecuencia debido a que los participantes bailan con el contenido frecuencial de cada tema musical.
Finalmente, para el género de reggaetón los resultados obtenidos se resumen en la tabla 5, donde se muestran la variación del coeficiente de Fourier y sus frecuencias asociadas. Los componentes dinámicos principales de la carga rítmica para dicho género son significativos hasta el tercer armónico. A diferencia de los géneros musicales anteriores, este se caracteriza por sostener una frecuencia principal similar a la de salto de una persona, ya que los dos pies tienden a estar en contacto con la plataforma al mismo tiempo.
En la figura 11 se muestra la gama de frecuencias asociadas a los coeficientes de Fourier, donde se pueden observar las amplitudes del armónico principal en 2.19 Hz, con un coeficiente de Fourier máximo de αmáx=0.98 y sus respectivos armónicos en 4.31 Hz, con un αmáx=0.19 y el tercero en 6.44 Hz con un αmáx=0.11.
3. CONCLUSIONES
La variación de la carga, debido a actividades rítmicas, depende en gran medida de diferentes factores como la sincronización, el ritmo de cada persona y el estado de ánimo al momento de la prueba. Debido a la combinación de estos elementos es posible explicar la dispersión observada en los resultados experimentales con situaciones de carga de real.
El análisis de los datos adquiridos en la plataforma experimental permitió establecer las frecuencias, factores de impacto y coeficientes de Fourier, para los géneros musicales considerados: salsa, merengue, bachata y reggaetón. Las mayores aceleraciones y factores de carga dinámicos se presentaron durante los tiempos de mayor sincronización de los participantes. Esto permitió establecer que la variación de la energía producida por la carga y la forma de la función de fuerza es proporcional a la altura de los saltos en las rutinas. Entre más alto sea el salto, mayor será el impacto sobre la estructura.
En la caracterización de las cargas de baile se observa que el segundo armónico de la fuerza producida por las personas en movimiento puede generar vibraciones en estructuras que poseen frecuencias naturales alrededor de 5 Hz el cual corresponde al límite establecido por la norma de diseño sismorresistente NSR-10 [14]. Por lo anterior se recomienda que el límite mínimo de frecuencia natural de sistemas de entrepiso usados como salones de baile o discotecas sea de 7.5 Hz con el fin de garantizar un buen desempeño en condiciones de servicio.
AGRADECIMIENTOS
Agradecemos a Colciencias por el apoyo económico brindado a este proyecto a través del Programa Jóvenes investigadores e innovadores, año 2011, a la Universidad Industrial de Santander y a Ecopetrol-Instituto Colombiano del Petróleo por el apoyo general que ha hecho posible el desarrollo de este estudio.
REFERENCIAS
[1] M. Setareh. Evaluation and assessment of vibrations owing to human activity. ICE publishing. Structures and Buildings, Vol 165, Pages 219–231, 2012.
[2] T. Murray, E. Allen and E. Ungar. Floor vibrations due to human activity. Design to prevent floor vibrations. Chicago: Engineering Journal/American Institute of Steel Construction. ISO 2631-2, 2003.
[3] L. Bruno y F. Venutti, ''Crowd-structure interaction in footbridges: Modelling, application to a real case-study and sensivity analyses''. Journal of Sound and Vibration, 475-493, 2009.
[4] S. Zivanovic, A. Pavic and P. Reynolds, ''Vibration serviceability of footbridges under human-induced excitation: a literature review''. Journal of Sound and Vibration, Vol. 279, No. 1-2, Pages. 1-74, 2005.
[5] A. Ortiz, D. Gómez, y P. Thomson, ''Caracterización del efecto de la interacción Humano-Estructura en el Estadio Olímpico en Cali, Colombia''. Ingeniería e Investigación, 29 (1), 2009.
[6] C.A. Jones, P. Reynolds, A. Pavic (2010). ''Review Vibration serviceability of stadia structures subjected to dynamic crowd loads: A literature review'', Journal of Sound and Vibration. Volume 330, Issue 8, Pages 1531–1566, 2011.
[7] B. R. Ellis and T. Ji, ''Floor vibration induced by dance-type loads: Verification''. The Structural Engineer, Volumen 72No. 3/1, 1994.
[8] S. Yao, J. R. Wright, A. Pavic, and P. Reynolds,. ''Experimental Study of Human-Structure Interaction for Jumping on a Perceptibly Moving Structure''. Journal of Sound and Vibration, Vol. 296, No. 1-2, pp. 150-165, 2006.
[9] B. R. Ellis and T. Ji, ''Floor vibration induced by dance-type loads: Theory''. The Structural Engineer, Volumen 72No. 3/1, 1994.
[10] H. Bachman et al. Vibration problems in structures: Practical guidelines. Boston: Library of congress cataloging in publication data, Birkhäuser, 1995a.
[11] K. Hong, ''Dynamic Load Factor for Floor Vibration due to Lively Concert''. Presentado en the 32nd International Congress and Exposition on noise Control Engineering Jeju International Convention Center. Seogwipo, Korea:, August 25-28, 2003.
[12] A. Ortiz, D. Gómez, y P. Thomson, ''Efectos de la interacción humano-estructura en las propiedades dinámicas de una tribuna'', Revista Ingeniería y Competitividad, Volumen 14, No. 1, p. 63 – 73, 2012.
[13] N. Alves, N. Roitman, y C. Magluta, ''Dynamic response under human movements''. Materials and Structures, 32, 31-37, 1999.
[14] AIS. Reglamento colombiano de construcción sismo resistente, NSR-10. Asociación Colombiana de Ingeniería Sísmica, 2011.