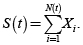
ARTÍCULOS

CONSTRUCCIÓN DE LA DISTRIBUCIÓN DE PÉRDIDAS Y EL PROBLEMA DE AGREGACIÓN DE RIESGO OPERATIVO BAJO MODELOS LDA: UNA REVISIÓN

CONSTRUCTION OF LOSS DISTRIBUTION AND OPERATING RISK AGGREGATION PROBLEM UNDER LDA MODELS: A REVIEW

Andrés Mora Valencia^**

^** Magíster en Ingeniería Industrial de la Universidad de los Andes, especialista en Matemáticas Avanzadas de la Universidad Nacional de Colombia e Ingeniero Industrial de la Universidad del Valle. Profesor Asistente de la Universidad EAFIT, Escuela de Economía y Finanzas, Departamento de Finanzas. E-mail: amvalencia@eafit.edu.co

Recibido: 22/03/2012
Aceptado: 25/10/2013

RESUMEN

Este artículo revisa la literatura más reciente en cuanto a la obtención de la distribución de pérdidas para riesgo operativo cuando se emplea el modelo de distribución de pérdidas agregadas (LDA, por sus siglas en inglés), y dependencia entre las líneas operativas. Cuando LDA es el método escogido para cuantificar riesgo operativo existen algunas cuestiones a resolver. Entre ellas está la obtención de la distribución de pérdidas, puesto que no existe una fórmula cerrada para obtenerla; sin embargo, existen métodos numéricos para resolver este problema. Finalmente, se presenta una revisión en cuanto a la obtención del riesgo operativo total de una entidad financiera, teniendo en cuenta la dependencia existente entre las diferentes líneas operativas.

PALABRAS CLAVE

Enfoque de distribución de pérdidas agregadas, valor en riesgo, agregación, cópulas.

ABSTRACT

This article performs a review of the most recent literature associated to the obtaining of loss distribution for operating risk when the LDA (Loss Distribution Approach) and dependency among operating lines is employed. When the LDA is the method of election to quantify operating risks, there are several questions to be solved, such as the obtaining of loss distribution, since there is not a closed formula to obtain it; however, there are numerical methods to solve this problem. Finally, a review associated to the obtaining of total operating loss of a financial entity is shown, bearing in mind the dependency among the existing operating lines.

KEY WORDS

Loss distribution approach; value at risk; aggregation.

INTRODUCCIÓN

En 2009, la OCC (US Office of the Comptroller of the Currency) reunió varios investigadores y profesionales dedicados al tema riesgo para discutir acerca de los desafíos más importantes que conlleva la cuantificación de riesgos. En cuanto a riesgo operativo, el resultado es un artículo divulgativo, denominado ''Operational Risk – Modeling the Extreme''. Uno de los hallazgos de este artículo es que el modelo más usado por la industria en Estados Unidos es la distribución de pérdidas agregadas (Loss Distribution Approach, LDA), y para obtener la distribución de pérdidas, Monte Carlo es el preferido. Métodos que combinan LDA con la teoría del valor extremo (EVT, por sus siglas en inglés), son los más empleados por los bancos. Sin embargo, la principal crítica que se le hace al modelo LDA es que tiende a subestimar la cola de la distribución de pérdidas, donde se presenta la mayoría de eventos de pérdida.

De acuerdo con Basilea, se requiere que las instituciones financieras calculen VaR al 99.9 % en un horizonte de un año como medida de riesgo operativo cuando se utiliza un enfoque de medición avanzada, como por ejemplo LDA. Para estimar este cuantil al 99.9 % se necesita la distribución de pérdidas agregadas y esta es la primera parte que trata este artículo, ya que realiza una revisión de los métodos numéricos existentes para obtener dicha distribución.

Un estudio de revisión en cuanto a cuantificación de riesgo operativo en Colombia fue realizado por Franco et al. [1] publicado en Revista Ingenierías de la Universidad de Medellín. De esta manera, a escala nacional, este artículo puede ser visto como la continuación de [1] y al de Mora [2]. Estos artículos tratan el problema de estimación de cuantiles altos para riesgo operativo y hacen una revisión de la literatura más importante en los métodos sugeridos (enfoque de indicador básico, enfoque estándar y enfoque de medición avanzada) por Basilea para cuantificar este tipo de riesgos. Existe una amplia literatura en administración de riesgo operativo como por ejemplo Cruz [3, 4], ; King [5], Alexander [6], Panjer [7], entre otros.

Este artículo se divide de la siguiente manera: la sección 1 describe brevemente el enfoque de distribución de pérdidas agregadas; la sección 2 trata de los métodos para obtener la distribución de pérdidas agregadas; la sección 3 revisa los trabajos más recientes en el tratamiento de dependencia entre las líneas operativas, y finalmente la sección 4 cierra con las conclusiones.

1. EL ENFOQUE DE LA DISTRIBUCIÓN DE PÉRDIDAS AGREGADAS (LDA)

Este enfoque consiste en estimar la distribución de pérdidas a partir de la combinación del proceso de frecuencia de eventos de pérdidas y el proceso de severidades. Este método tiene sus raíces en la actuaría, donde se desea calcular las pérdidas de una aseguradora por reclamos. Sea S(t) la suma agregada de pérdidas dada por:

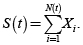
• Donde X_i representa las pérdidas generadas por eventos de riesgo operativo. Por lo general, se asume una distribución continua para simular el proceso de severidades. Si se cuenta con suficientes datos históricos se procede a ajustar una distribución paramétrica a los datos, de lo contrario se puede usar datos externos.

• N(t) representa el proceso de recuento, es decir, la frecuencia de eventos de pérdida y por lo general se asume una distribución discreta para simular este proceso. Generalmente se usa la distribución Poisson; sin embargo, se puede utilizar la binomial negativa o mixturas de distribuciones Poisson para simular sobre-dispersión.

El enfoque LDA puede arrojar mayor o menor requerimiento de capital dependiendo de la entidad; sin embargo, en estudios de Haubenstock y Hardin [8], el enfoque LDA presenta menores cargos de capital que los enfoques de indicador básico y estándar. Para combinar los dos procesos (de frecuencia y severidad) y obtener la distribución de pérdidas agregadas, lo más simple es utilizar una simulación Monte Carlo, pero existen otros métodos como la transformada rápida de Fourier (FFT, por sus siglas en inglés) o recursión de Panjer, que serán objeto de estudio en la primera parte de este artículo. El enfoque LDA es explicado en detalle por Frachot et al. [9], mientras que Aue y Kalkbrener [10] lo aplican a Deutsche Bank. Un ejemplo sencillo de cómo se emplea el enfoque LDA se encuentra en la sección 8.5 de [8], quienes modifican datos reales de una entidad financiera para asegurar confidencialidad.

2. CONSTRUCCIÓN DE LA DISTRIBUCIÓN DE PÉRDIDAS

El proceso de calcular la distribución de pérdidas agregadas conlleva analizar métodos numéricos, puesto que en este proceso se obtienen convoluciones de la distribución de pérdida que no son tratables desde el punto de vista analítico. Entonces, existen varios métodos para obtener la distribución de pérdidas agregadas cuando se utiliza el método LDA. Entre ellos están la transformada rápida de Fourier (Robertson [11] y Wang [12]), la simulación Monte Carlo y la recursión de Panjer [13]. En la mayoría de estudios en riesgo operativo, se observa que el método preferido es la simulación Monte Carlo por su facilidad, pero, por ejemplo, Mignola y Ugoccioni [14] utilizan FFT. Algunos textos que discuten los métodos mencionados anteriormente son [7] y Klugman et al. [15]. Embrechts et al. [16] detallan los métodos más importantes en la obtención de distribución de pérdidas que se describen brevemente a continuación.

• Métodos recursivos

El método más conocido en el área de seguros es el método recursivo de Panjer. Para emplear este método, es necesario que la distribución de la severidad sea discreta, pero si es continua se necesita discretizarla. Técnicas de discretización se pueden encontrar en la sección 6.15 de Panjer y Willmot [17].

• Métodos de inversión

Dentro de estos métodos se encuentra FFT que es un algoritmo para invertir la función característica y así obtener densidades de variables aleatorias discretas.

• Métodos de aproximación

Se pueden usar distribuciones paramétricas como por ejemplo la normal y otras asimétricas como el caso de la gamma trasladada y Pareto generalizada. Existen otros tipos de aproximaciones como la expansión de Edgeworth y por punto de silla (saddlepoint).

• Métodos de simulación

Aparte de la simulación Monte Carlo, también se puede realizar un bootstrapping para obtener la distribución de las pérdidas agregadas. Un algoritmo para obtener la distribución de pérdidas mediante este método se puede encontrar en la sección 7.6 de [6] y Reynolds y Syer [18].

a) Recursión de Panjer

Sea:

p_k = P[N = k] la probabilidad de los eventos de pérdida.

f_k = P[X_i = k] la probabilidad de las severidades.

g_k = P[S = k] la probabilidad de la pérdida agregada, como se vio anteriormente,

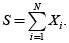
Además suponga que: g₀ = P[S = 0] = P[N = 0] = p₀

Esto es, si no hay eventos, no hay pérdida. Entonces, se dice que N pertenece a la clase Panjer (a,b) si:

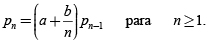
Las distribuciones que cumplen con esta clase son la binomial, binomial negativa y Poisson. Los valores de a y b que cumplen la clase de Panjer son:

• Distribución Binomial(n,p):

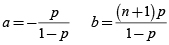
• Distribución Binomial Negativa(α,p):

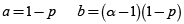
• Distribución Poisson(λ):

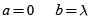
Entonces, el algoritmo para encontrar los valores de pérdida agregada está dado por:

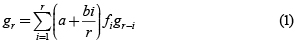
b) Métodos de inversión

La transformada rápida de Fourier (FFT) es un algoritmo utilizado para invertir la función característica 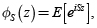para obtener densidades de variables aleatorias discretas. Para calcular las probabilidades se utiliza la siguiente relación:

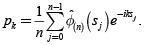
Para más detalles del cálculo de probabilidades a través de este método se puede consultar por ejemplo Embrechts y Klüppelberg [19], Grübel y Hermesmeier [20]. El siguiente gráfico reproduce la figura 1 de Embrechts y Frei [21], donde se asume que las pérdidas siguen una distribución Pareto(4,3) y las frecuencias una distribución Poisson(20).

Para el método recursivo de Panjer se utilizó el método de redondeo para discretizar la distribución Pareto. Un ejemplo reciente de uso de estos métodos es el de Jang y Fu [22], quienes obtienen una expresión analítica de las transformadas de Laplace de las distribuciones de la pérdida agregada y luego invierten sus transformadas rápidas de Fourier para calcular medidas de riesgo. Los autores emplean las distribuciones loggamma, Fréchet y Gumbel truncada para simular las distribuciones de severidad con la característica de presentar colas pesadas, y exponencial que no presenta colas pesadas. Para el proceso de frecuencia se usa un proceso de Poisson homogéneo y un proceso de Cox. El primer caso es un proceso con intensidad (tasa de llegada) constante, mientras que en el proceso de Cox la intensidad depende del tiempo, pero además es estocástica.

c) Aproximaciones

Suponga que el monto de las pérdidas es i.i.d. e independientes del proceso de frecuencia de eventos, y retome que las pérdidas agregadas son:

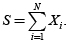
El valor esperado de las pérdidas agregadas está dado por E[S] = μE[N].

Donde μ es el valor esperado de la distribución de pérdidas y E[N] el valor esperado de la frecuencia de los eventos. La varianza de las pérdidas agregadas está dada por:

var[S] = var[N]μ + E[N]var[X]

Donde var[N] es la varianza del proceso de frecuencia y var[X] es la varianza de la distribución de las pérdidas, que es equivalente a μ₂-μ², donde μ₂ es el segundo momento de la distribución de pérdidas.

• Aproximación a la normal

Se puede entonces utilizar una aproximación normal para las pérdidas agregadas:

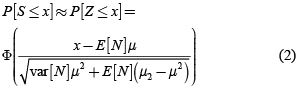
Donde Φ es la distribución acumulada de una normal estándar. Si se asume que las frecuencias siguen una distribución Poisson, donde E[N] = var[N] = #&955;, entonces:

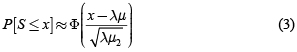
Para el caso del gráfico anterior (figura 1), donde se asume que las pérdidas siguen una distribución Pareto(4,3) y la frecuencia Poisson(20), los valores faltantes son μ = 1 y μ₂ = 3. Con estos valores se grafica la densidad con la aproximación normal y se compara con la densidad obtenida mediante la recursión de Panjer.

El problema, como se ve en el gráfico anterior, es que las distribuciones de pérdida pueden ser sesgadas y la normal es una distribución simétrica; por ende, no brindaría un buen ajuste. Para ello se propone el uso de la distribución gamma como una mejor aproximación.

• Aproximación a la gamma

Otra propuesta es aproximar las pérdidas agregadas a k + G donde k es una constante y G es una distribución gamma Γ(γ,α) con parámetro de forma γ y de escala α. Puesto que a la distribución gamma se le adiciona la constante k, esta aproximación también recibe el nombre de gamma trasladada. La idea consiste en coincidir los tres primeros momentos de la distribución gamma con los de la pérdida agregada. Sea m, σ y β el valor esperado, la varianza y el coeficiente de asimetría de las pérdidas agregadas, entonces los parámetros de la distribución gamma y la constante k se pueden expresar como:

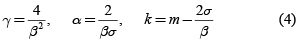
El siguiente gráfico muestra la aproximación de la gamma trasladada con los mismos datos del ejemplo en los gráficos anteriores. Se puede mostrar que μ₃ = 27.

Al compararla con la aproximación normal, se observa que la gamma trasladada ofrece una mejor aproximación a la distribución de pérdidas agregadas.

d) Simulación

El método más sencillo de obtener pérdidas agregadas es la simulación Monte Carlo y a continuación se presenta una comparación de las densidades con el método recursivo de Panjer.

Como se observa en la anterior figura, entre más datos se simulen, se obtiene una mejor aproximación a la distribución de pérdidas agregadas. Para una comparación en velocidad y confiabilidad de simulación Monte Carlo, métodos de recursión y FFT, ver Temnov y Warnung [23]. Peters y Sisson [24] y Peters et al. [25] emplean simulación Monte Carlo de Cadenas de Markov (MCMC, por sus siglas en inglés) y modelos bayesianos para estimación de parámetros y la obtención de la distribución de pérdidas agregadas. Los autores aconsejan usar estas técnicas puesto que son más eficientes que los métodos tradicionales de simulación Monte Carlo.

Comentarios

Para más detalles de los métodos de recursión y FFT como sus problemas, ver [21] y las referencias allí contenidas. Aunque el algoritmo recursivo de Panjer ha sido ampliamente usado en actuaría y presenta una aproximación confiable a la distribución de pérdidas agregadas, los autores reconocen que FFT posee dos ventajas sobre este algoritmo. Una es que funciona con cualquier tipo de distribución discreta, puesto que la recursión de Panjer solo funciona para distribuciones binomial, binomial negativa y Poisson. Otra ventaja de FFT es que es mucho más eficiente. Un método que mejora algunos de los problemas de recursión de Panjer es presentado en Guégan y Hassani [26].

Otro artículo donde se realizan comparaciones de los métodos mencionados es el de Shevchenko [27], quien concluye que cada método tiene sus fortalezas y debilidades. Por ejemplo, la simulación Monte Carlo es lenta pero es fácil de implementar y permite modelar dependencia. Esta última característica no es fácil de incluir en los métodos de FFT y Panjer; sin embargo, el método de Panjer es el más fácil de implementar aunque incluye error de discretización. El método de FFT es generalmente más rápido. A continuación se presenta la segunda parte del artículo que respecta a la revisión de literatura de métodos de agregación.

3. CÓPULA COMO MÉTODO DE AGREGACIÓN DE RIESGOS

El problema de agregación involucra la dependencia que puede existir entre los tipos de riesgo y líneas de negocio. Al existir dependencia en las líneas de negocio, y si se calcula el cargo de capital como la suma de los VaR individuales, puede ocurrir una sobre-estimación del verdadero cargo. Si las severidades presentan distribuciones con colas pesadas, el VaR puede violar la propiedad de subaditividad, y por ende, obtener un cargo de capital subestimado. Al obtener el VaR al 99.9 % de cada línea operativa por tipo de riesgo, los bancos pueden obtener el cargo por capital total (CxC^RO), sumando todos los VaR y aplicar un factor de diversificación δ, de acuerdo con Basilea (Sección 657 y 669 (d) de BCBS [28]). En la práctica, los bancos reclaman que δ esté entre el 10 % y 30 %. Esto es:

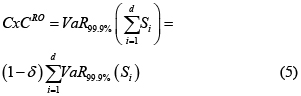
Donde S_i denota la pérdida por riesgo operativo anual en cada línea operativa i para todas las d líneas. Y δ es un porcentaje por beneficios de diversificación.

Neslehová et al. [29] encuentran que bajo modelos de ''media infinita''¹, los bancos no podrían justificar beneficios de diversificación, puesto que el VaR es no subaditivo (ver Artzner et al. [30]). Para el caso específico de riesgo operativo, esto es:

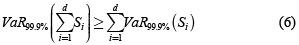
El artículo de Degen et al. [31] realiza sensibilidades de los beneficios de diversificación con respecto a niveles de confiabilidad al cual se desea estimar el VaR con severidades distribuidas Pareto, Burr y g-h. Uno de los principales resultados del artículo es que no solamente para modelos de media infinita se obtiene la violación del axioma de subaditividad del VaR, pero podría darse también con modelos de media finita (por ejemplo, distribución Burr con parámetros τ = 0.25 y κ = 8, y distribución g-h con parámetros g = 2 y h = 0.5). Es decir, agregar riesgos puede conllevar beneficios negativos de diversificación sin importar cuán pesada es la cola de la distribución de las pérdidas cuando se estima VaR.

Pueden existir varios tipos de dependencia en las celdas, y Böcker y Klüppelberg [32] realizan en la primera sección una revisión de la literatura acerca de estos tipos de dependencia. Los autores encuentran que modelar dependencia en la frecuencia de pérdida no es tan relevante. En aplicaciones financieras la medida estadística más utilizada para medir dependencia es la correlación lineal; sin embargo, esta medida solo captura dependencia lineal. Embrechts et al. [33] señalan que el uso de correlación lineal no trae problemas cuando los factores de riesgo se distribuyen normal, pero en la mayoría de riesgos financieros este no es el caso. Para solucionar este y otros problemas, se propone el uso de otras medidas de correlación (basadas en rangos) o el uso de cópulas. Las cópulas representan una manera de extraer la estructura de dependencia de una distribución conjunta. Para una discusión de las ventajas y desventajas del uso de cópulas frente a correlación, ver por ejemplo Moosa [34]. Acerca de cópulas existe una amplia literatura, entre ellos están: Joe [35], Nelsen [36], Cherubini et al. [37], Trivedi y Zimmer [38], Fredheim [39], Rank [40], entre otros.

Una cópula puede ser vista como una función para obtener una distribución conjunta a partir de dos o más funciones de distribución marginal. La representación más conocida se debe a Sklar [41]: .

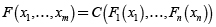Donde F es la distribución conjunta, F₁,..., F_n son las distribuciones marginales y C es la cópula. Si las distribuciones marginales son continuas, entonces la cópula es única.

Dependencia de las pérdidas por riesgo operativo entre las diferentes líneas operativas se pueden obtener de diferentes maneras. Una manera es tener en cuenta la dependencia en la frecuencia de eventos vía cópulas. Algunos de estos estudios son: [9], [10] y Bee [42]. Otra manera es tener en cuenta dependencia entre las severidades anuales mediante cópulas, y es la que se presenta en este artículo. A continuación se detallan algunos de estos estudios más recientes.

El-Gamal et al. [43] utilizan datos de un banco (del The 2004 Operational Risk Loss Data Collection Exercise-LDCE) y la cópula-t, puesto que permite modelar colas pesadas y mayor dependencia en las colas. Para las marginales se utiliza una distribución cuyo cuerpo es lognormal y en las colas la distribución de Pareto generalizada (GPD, por sus siglas en inglés). Finalmente, los autores obtienen como resultado una diversificación entre 0.5 % y 10.7 % en sus cálculos de VaR. Otro estudio que utiliza la cópula-t es el de Giacometti et al. [44]. Los autores utilizan distribuciones de colas pesadas para simular severidades, un proceso de Poisson no homogéneo para las frecuencias y emplean dos casos de cópulas. Una la tradicional t y otra t-sesgada al caso de un banco europeo. Uno de los resultados del artículo es que la reducción de capital que se obtiene al usar severidades con colas cortas o medianas en las marginales de la cópula es menor a la reducción obtenida con marginales de colas pesadas. Al estimar VaR al 99.9 % los resultados arrojan una reducción de cargo de capital entre el 21 % y el 30 % mediante las cópulas t y t-sesgada. Lee y Fang [45] también utilizan cópulas Gaussiana, t y Clayton en bancos comerciales de Taiwan.

Para modelar dependencia entre frecuencia y severidad en las diferentes celdas, [32] usan la cópula Lévy. Para ello, asumen que el proceso de frecuencia sigue un proceso de Poisson homogéneo y todas las severidades son iid. Uno de los resultados más importantes de su artículo es la extensión del caso univariado LDA de una celda a un modelo de Poisson compuesto multivariado. El VaR puede ser obtenido mediante simulación, puesto que no existe una fórmula cerrada en este caso.

Un estudio que se enfoca en las diferencias de cálculo de VaR al 99.9 % entre la agregación por tipo de línea operativa y agregación por tipo de riesgo es el realizado por Embrechts y Puccetti [46]. Los autores llaman a esta diferencia #&948; y estiman tres casos donde modelan dependencia entre severidades como también entre frecuencias. Este último caso no es tan sencillo, puesto que las marginales no son distribuciones continuas. Para un tratamiento de este tipo de cópulas se recomienda ver el artículo de Genest y Ne lehová [47]. Para el proceso de frecuencia se asume un proceso de Poisson homogéneo con parámetro λ igual a 20 y se utilizan severidades con distribuciones lognormal y Pareto con un índice de cola entre 1 y 4. Esto quiere decir que no se utilizan modelos de media infinita. El principal resultado de [46] es que λ disminuye a medida que se incrementa la dependencia. Adicionalmente, esta diferencia disminuye más con interdependencia entre las severidades que entre las de frecuencia.

Un estudio que sí involucra modelos de media infinita es el de Abbate et al. [48], donde los autores emplean la base de datos de cuatro años de un banco. Los autores usan distribuciones de severidad donde el cuerpo es lognormal y las colas GPD, y el proceso de frecuencia sigue un modelo Poisson homogéneo. Al estimar el índice de cola de las distribuciones, se encuentra que una línea operativa sigue un modelo de media infinita. Al seguir la recomendación de Basilea, de obtener el VaR por líneas operativas, se encuentra que el VaR no es coherente a varios niveles de confiabilidad, al incluir la línea operativa con distribución de media infinita. Esta no subaditividad conduce a subestimaciones del VaR en el caso de perfecta dependencia (llamado también caso comonotónico), lo cual es consistente con un hallazgo previo de Embrechts y Puccetti [49]. Uno de los principales resultados de este artículo es que para modelos de media finita, el VaR es subaditivo, y agregar pérdidas mediante cópulas ayuda disminuir el cargo por capital, mientras que para modelos de media infinita, VaR no es coherente, y por ende, conduce a que las cópulas no reducen cargo de capital. Es decir, para el último caso no hay beneficios de diversificación. [48] también prueban las cópulas Frank y Cook-Johnson, pero no encuentran mucha diferencia en los estimados de cargos de capital con estas dos cópulas.

Comentarios

Modelar dependencia entre pérdidas es aún un desafío en riesgo operativo. En la revisión de la literatura se observa que la técnica más utilizada es cópulas. Se debe tener especial cuidado con el uso de cópulas al querer reducir los estimados de cargos de capital en un gran porcentaje. La revisión de la literatura muestra que se pueden lograr grandes reducciones en el VaR total de una entidad financiera (en especial cuando las distribuciones no tienen colas tan pesadas); sin embargo, se debe usar la cópula adecuada para modelar la dependencia entre las líneas de negocios. Cuando se presenta el caso de distribuciones de pérdida con colas muy pesadas, el VaR es no subaditivo, y por ende, dependencia puede conducir a subestimaciones en los cargos de capital.

Sin embargo, aun para algunos casos donde la distribución no exhibe colas tan pesadas, el VaR puede ser no subaditivo como lo muestran [31]. Se observa que en la mayoría de los estudios se utiliza la distribución GPD para ajustar la cola de las marginales (de las pérdidas). La cópula gaussiana es muy empleada, pero tiende a subestimar capital de riesgo, por no capturar de manera efectiva los eventos de cola. Por lo tanto, se compara con la cópula t, puesto que esta cópula soluciona el problema de la cópula gaussiana cuando los grados de libertad son bajos. Los autores argumentan que esta distribución se ajusta mejor en las colas de las pérdidas que otras distribuciones.

4. CONCLUSIONES

Bajo el enfoque LDA existen varios métodos para construir la distribución de pérdidas agregadas. La simulación Monte Carlo es el método más sencillo y usado en la práctica, pero es lento. Métodos de Panjer también son sencillos de implementar, pero incluyen error de discretización y FFT es rápido desde el punto de vista computacional, pero no es tan sencillo de implementar como los otros métodos. En cuanto a dependencia, si los bancos desean persuadir al regulador de obtener beneficios por diversificación, deben emplear una técnica convincente. El uso de cópulas es adecuado en la agregación de riesgos y captura dependencia. Sin embargo, los beneficios de diversificación, al usar una medida como VaR, se pueden desvanecer dependiendo del comportamiento de las colas de las distribuciones de pérdida. Es por esto que se sugiere comenzar a revisar otras medidas de riesgo. En principio, expected shortfall puede ser una buena alternativa, pero esta medida no existe en modelos de media infinita. Por ejemplo, Heyde et al. [50] recomiendan el uso de la mediana condicional de la cola, también sugerido por Moscadelli [51].

Notas

1 Estos modelos son llamados así porque las colas de las distribuciones son muy pesadas y puede conllevar a estimación de cargos de capital absurdos mediante VaR. Bajo estos modelos, medidas como expected shortfall no tienen sentido. Para más detalles y discusión de estos modelos, ver [29].

REFERENCIAS

[1] L. C. Franco, J. G. Murillo, et al., ''Riesgo Operacional: Reto actual de las entidades financieras''. Revista Ingenierías Universidad de Medellín. Vol. 5, no. 9, pp. 97-110, 2006.

[2] A. Mora, ''Consideraciones en la estimación de cuantiles altos en riesgo operativo''. Análisis – Revista del Mercado de Valores. Número 1, pp. 181-216, 2010.

[3] M. Cruz, Modelling, Measuring and hedging operational risk. Wiley, Chichester, 2002.

[4] M. Cruz (editor), Operational risk modelling and analysis: Theory and Practice. Risk Waters Group, London, 2004.

[5] J. King, Measurement and modelling operational risk. Wiley, 2001.

[6] C. Alexander, ''Statistical models of operational loss'', in Alexander C. (2003), pp. 129-170. Operational Risk: Regulation, Analysis and Management, Prentice Hall, Upper Saddle River, NJ, 2003.

[7] H. Panjer, Operational risk: Modeling analytics. Wiley Series in Probability and Statistics, 2006.

[8] M. Haubenstock y L. Hardin, ''The loss distribution approach'', in Alexander C. (2003), pp. 229-240, Operational Risk: Regulation, Analysis and Management, Prentice Hall, Upper Saddle River, NJ, 2003.

[9] A. Frachot, O. Moudoulaud y T. Roncalli, ''Loss distribution approach in practice''. The Basel Handbook: A Guide for Financial Practitioners. Ong, M. (ed). Risk Books, London, pp. 527-554, 2004.

[10] F. Aue y M. Kalkbrener, ''LDA at work: Deutsche Bank's approach to quantifying operational risk'', Journal of Operational Risk, 1(4), 49-93, 2006.

[11] J. Robertson, ''The computation of aggregate loss distributions'', PCAS LXXIX pp. 57-133, 1992.

[12] S. Wang, ''Aggregation of correlated risk portfolios: Models and algorithms'', Report. Disponible: www.casact.org/cotor/wang.pdf, 1998.

[13] H. Panjer, ''Recursive evaluation of a family of compound distributions'', ASTIN Bulletin, 12, 22-26, 1981.

[14] G. Mignola y R. Ugoccioni, ''Sources of uncertainty in modeling operational risk losses''. Journal of Operational Risk, Vol. 1, N° 2, 33-50, 2006.

[15] S. A. Klugman, H. Panjer, y G. E. Willmot, Loss models: From data to decisions. Wiley, 1998.

[16] P. Embrechts, Furrer, H. y R. Kaufmann, ''Quantifying regulatory capital for operational risk''. Derivatives Use, Trading & Regulation, 9(3): 217-233, 2003.

[17] H. Panjer y G. Willmot, Insurance risk models, Society of Actuaries, Schaumberg, IL, 1992.

[18] D. Reynolds y D. Syer, ''A general simulation framework for operational loss distributions''. En C. Alexander, Operational Risk: Regulation, Analysis and Management, Prentice Hall, Upper Saddle River, NJ, pp. 193-214, 2003.

[19] P. Embrechts y C. Klüppelberg, ''Some aspects of insurance mathematics''. Theory of Probability and its Applications, 38 pp. 262-295, 1994.

[20] R. Grübel, y R. Hermesmeier, ''Computation of compound distributions II: discretization errors and Richardson exptrapolation''. ASTIN Bulletin 30, 309-331, 1999.

[21] P. Embrechts y M. Frei, ''Panjer recursion versus FFT for compound distributions''. Mathematical Methods of Operations Research, 69(3):497-508, 2009.

[22] J. Jang y G. Fu, ''Transform approach for operational risk modeling: Value-at-Risk and Tail Conditional Expectation''. Journal of Operational Risk, 3 N° 2, 2008.

[23] G. Temnov y R. Warnung, ''A comparison of loss aggregation methods for operational risk''. Journal of Operational Risk, 3 N° 1, 2008.

[24] G. Peters W. y S. Sisson, ''Bayesian inference Monte Carlo sampling and operational risk''. Journal of Operational Risk, 1, N° 3, 2006.

[25] G. W. Peters, A. M. Johansen y A. Doucet, ''Simulation of the annual loss distribution in operational risk via Panjer recursions and Volterra integral equations for value at risk and expected shortfall estimation''. Journal of Operational Risk, 2, N° 3, 2007.

[26] D. Guégan y B. Hassani, ''A modified Panjer algorithm for operational risk capital calculations''. Journal of Operational Risk, 4 N° 4, 2009.

[27] P. V. Shevchenko, ''Calculation of aggregate loss distributions''. The Journal of Operational Risk, 5(2), pp. 3-40, 2010.

[28] BCBS, ''International convergence of capital measurement and capital standards: A revised framework''. Bank for International Settlements, Basel, 2006.

[29] J. Neslehová, V. Chavez-Demoulin, y P. Embrechts, ''Infinite-mean models and the LDA for operational risk''. Journal of Operational Risk, 1 (1) pp. 3-25, 2006.

[30] P. Artzner, F. Delbaen, J. M. Eber y D. Heath, ''Coherent measures of risk''. Mathematical Finance 9: 203-228, 1999.

[31] M. Degen, D. Lambrigger, y J. Segers, ''Risk concentration and diversification: Second-order properties''. Insurance: Mathematics and Economics, 46: 541-546, 2010.

[32] K. Böcker, y C. Klüppelberg, ''Modeling and measuring multivariate operational risk with Lévy copulas''. Journal of Operational Risk, 3 N° 2, 2008.

[33] P. Embrechts, A. J. McNeil y D. Straumann, ''Correlation: Pitfalls and alternatives A short, non-technical article'', RISK Magazine, May, 69-71, 1999.

[34] I. A. Moosa, Operational risk management. London: Palgrave, 2007.

[35] H. Joe, Multivariate models and dependence concepts. Chapman & Hall, London, 1997.

[36] R. B. Nelsen, An introduction to copulas. Springer, New York, 1999.

[37] U. Cherubini, E. Luciano y W. Vecchiato, Copula methods in finance. Wiley, 2004.

[38] P. K. Trivedi y D. M. Zimmer, Copula modeling: An introduction for practitioners. Now Publishers Inc, 2007.

[39] M. Fredheim, Copula methods in finance. VDM Verlag, 2008.

[40] J. Rank, Copulas: From theory to application in finance. Risk Books, 2006.

[41] A.Sklar, ''Fonctions de répartition à n dimensions et leurs marges'', Publications de l'Institut de Statistique de L'Université de Paris, 8, pp. 229-231, 1959.

[42] M. Bee, ''Copula-based multivariate models with applications to risk management and insurance''. Working Paper, Università degli Studi di Trento, 2005.

[43] M. El-Gamal, H. Inanoglu, y M. Stengel, ''Multivariate estimation for operational risk with judicious use of extreme value theory''. Journal of Operational Risk, 2 N° 1, 2007.

[44] R. Giacometti, S. Rachev, A. Chernobai, y M. Bertocchi, ''Aggregation issues in operational risk''. Journal of Operational Risk, 3 N° 3, 2008.

[45] W.-C. Lee y C.-J. Fang, ''The measurement of capital for operational risk in Taiwanese commercial banks''. Journal of Operational Risk, 5 (2) pp. 79-102, 2010.

[46] P. Embrechts y G. Puccetti, ''Aggregating risk across matrix structured loss data: the case of operational risk''. Journal of Operational Risk 3(2), 29-44, 2008.

[47] C. Genest y J. Neslehová, ''A primer on copulas for count data''. The Astin Bulletin, 37, 475-515, 2007.

[48] D. Abbate, W. Farkas y E. Gourier, ''Operational risk quantification using extreme value theory and copulas: From theory to practice''. Journal of Operational Risk, 4 N° 3, 2009.

[49] P. Embrechts y G. Puccetti, ''Aggregating risk capital, with an application to operational risk''. The Geneva Risk and Insurance Review, 31(2): 71–90, 2006.

[50] C.C. Heyde, S.G. Kou y X.H. Peng, ''What is a good risk measure: Bridging the gaps between data, coherent risk measures, and insurance risk measures''. Columbia University. Preprint, 2006.

[51] M. Moscadelli, ''The modelling of operational risk: Experience with the analysis of the data collected by the Basel Committee''. Technical Report 517. Banca d'Italia, 2004.