
ARTÍCULOS
VALORACIÓN DE PROYECTOS DE ENERGÍA TÉRMICA BAJO CONDICIONES DE INCERTIDUMBRE A TRAVÉS DE OPCIONES REALES
VALUATION OF THERMAL ENERGY PROJECTS UNDER UNCERTAINTY CONDITIONS THROUGH REAL OPTIONS
Mónica A. Arango Arango*; Elizabeth T. Arroyave Cataño**; Juan D. Hernández***
* Economista, Universidad de Antioquia, Medellín, Colombia. Candidata a Doctora en Ingeniería Industria y organizaciones, Universidad Nacional de Colombia. Magíster en Administración Financiera y Magíster en Finanzas, Universidad EAFIT, Medellín, Colombia. Especialista en Finanzas, Universidad EAFIT, Medellín, Colombia. Profesora tiempo completo, Programa de Ingeniería Financiera, Universidad de Medellín, Medellín, Colombia. Miembro activo del Grupo de Investigación en Ingeniería Financiera GINIF. Carrera 87 N° 30 - 65 Medellín, Colombia. Teléfono +57(4) 3405288. Correo electrónico: moarango@udem.edu.co
** Administrador de negocios, Universidad EAFIT, Medellín, Colombia. Magíster en Administración Financiera y Magíster en Finanzas, Universidad EAFIT, Medellín, Colombia. Especialista en Finanzas, Universidad EAFIT, Medellín, Colombia. Profesora tiempo completo, Programa de Ingeniería Financiera, Universidad de Medellín, Medellín, Colombia. Miembro activo del Grupo de Investigación en Ingeniería Financiera GINIF. Carrera 87 N° 30 - 65 Medellín, Colombia. Teléfono +57(4) 3405420. Correo electrónico: etarroyave@udem.edu.co
*** Contador Público, Universidad de Antioquia, Medellín, Colombia. Magíster en Finanzas, Universidad EAFIT, Medellín, Colombia. Catedrático, Programa de Ingeniería Financiera, Universidad de Medellín, Medellín, Colombia. Carrera 87 N° 30 - 65 Medellín – Colombia. Teléfono: 3405233. Correo: jdhernandez@udem.edu.co
Recibido: 14/05/2013
Aceptado: 25/10/2013
RESUMEN
Este trabajo valora una planta a base de carbón para la generación de energía térmica en un país latinoamericano considerando sus opciones reales. El trabajo presenta, en primer lugar, el comportamiento probabilístico de cada una de las variables que afectan la viabilidad financiera del proyecto. Para ello, se proponen modelos ARIMA-GARCH que permiten pronosticar las medias y la volatilidad de las variables que determinan el flujo de caja. Debido a la alta volatilidad en los precios de la energía y al incremento del precio internacional del carbón en los últimos años, se espera que estos proyectos no sean viables financieramente. Sin embargo, al considerar las opciones reales de expansión, de abandono y de continuar puede dar como resultado escenarios en los cuales esta tecnología sea competitiva. Los resultados obtenidos sugieren disminución de los riesgos de pérdida e incremento del valor del proyecto.
PALABRAS CLAVE
Opciones reales, valoración, simulación Monte Carlo, energía.
ABSTRACT
This article shows the valuation of carbon-based plant for generation of thermal energy in a Latin American country, taking real options into consideration. The work first shows the probabilistic behavior of each variable which affects financial viability of the project. For this purpose, ARIMA-GARCH models which allow foreseeing means and volatility of variables which determine the cash flow are proposed. Due to the high volatility of energy prices and the increased international price of carbon during the last years, these projects are not expected to be financially viable. However, when considering the real option to expansion, abandonment and continue can result scenarios in which this technology is competitive. Results obtained suggest a decrease of loss risks and an increase of the project value.
KEY WORDS
Real options; valuation; Monte Carlo simulation; energy.
INTRODUCCIÓN
En el año 2006 Colombia contaba con un parque de generación de energía eléctrica compuesto principalmente por plantas hídricas, con una capacidad que representaba el 64.1% del total de la capacidad efectiva del Sistema Interconectado Nacional (SIN); el resto de la generación se encontraba representada por un 32.1% en térmica y un 3.8% en otros tipos de generación. A enero de 2012 Colombia cuenta con un parque de generación de energía eléctrica compuesto, de un 78.4% hidráulica, 15.4% térmica y 6.2% para menores y cogeneradores, lo que evidencia que la generación de energía hidráulica es aún la de mayor participación en Colombia. La posición geográfica y la riqueza hídrica del país han permitido el desarrollo de la energía hidráulica, posicionándola como la mayor fuente en el mercado energético nacional, lo que constituye un riesgo al depender principalmente de esta alternativa de generación de energía. Si bien es importante para el país el desarrollo del sector eléctrico a partir de su riqueza hídrica, esta dependencia podría atentar contra la confiabilidad de la prestación continua y sostenible del servicio, considerada como una de las principales preocupaciones del Gobierno después de la crisis energética de los noventa.
Esta realidad ha motivado el interés del Estado colombiano por crear mecanismos e incentivar inversiones en combustibles sustitutos para la generación de energía que aseguren la disponibilidad para cubrir la demanda creciente. Una alternativa complementaria a la generación de energía hidráulica consiste en la producción de energía térmica a través de carbón como combustible. Esta alternativa de generación es de gran confiabilidad para el sistema interconectado nacional, pues existe garantía de reservas del carbón en el largo plazo, y la generación a través de este combustible no depende de las condiciones climáticas del país, como es el caso de las fuentes hídricas.
La evidencia empírica en Colombia indica que la generación térmica actúa como un bien complementario en época de sequía. Según el Ministerio de Minas y Energía de Colombia [1] durante 2010, la composición hidráulico-térmica de la generación estuvo impactada por la finalización del fenómeno climático El Niño en el primer trimestre, acompañado de bajos aportes hídricos, y el desarrollo del fenómeno La Niña en el segundo semestre, asociado con altos aportes. El impacto combinado de ambos fenómenos climáticos sobre los aportes hídricos al Sistema Interconectado Nacional, SIN llevó a finalizar un año en condiciones hídricas promedio, con aportes totales anuales de 52.302,1 GWh equivalentes al 106,9% del promedio histórico. Fue así como la generación térmica participó en la generación del SIN hasta en un 53,3% (enero de 2010) en pleno desarrollo de El Niño.
Considerando las diferentes tecnologías de generación de energía existentes, se hace necesario evaluar cada una de estas de acuerdo con la disponibilidad de recursos naturales y las necesidades del país. En este sentido, se resalta la importancia de evaluar la factibilidad financiera de la implementación de proyectos de generación de energía térmica. Cada una de las tecnologías de generación de energía térmica tiene características específicas en términos de costos, operación, escala requerida, tiempo de construcción y vida útil, flexibilidad o impactos sociales y ambientales. El presente trabajo pretende evaluar a través de opciones reales la factibilidad financiera de desarrollar un proyecto de generación de energía térmica empleando carbón. Siendo este una fuente alterna de generación de energía especialmente en períodos de sequía, se convierte en una alternativa ideal al buscar garantizar la sostenibilidad, la confiabilidad y la seguridad del sistema eléctrico.
En este trabajo se valora financieramente una planta de generación de energía térmica en condiciones de incertidumbre. En primer lugar, se construye un marco teórico sobre la teoría de opciones reales y la utilización de esta metodología en proyectos de estas características. En segundo lugar, se hace la valoración del proyecto bajo incertidumbre utilizando la metodología de opciones reales, donde se concluye que el proyecto por sí solo es de alto riesgo, y en muchas trayectorias, inviable financieramente. Sin embargo, al considerar la flexibilidad de las decisiones, existen trayectorias donde puede ser una alternativa financieramente viable y complementaria a la energía hidráulica. Por último, se plantean propuestas de investigación que surgen de los resultados encontrados.
1. MARCO TEÓRICO
La evolución del mercado eléctrico ha motivado el desarrollo de múltiples investigaciones que abordan el análisis desde diferentes perspectivas: en primer lugar, se encuentra el interés por abordar los temas de regulación, que tienen efectos en los mercados del sector, ya que influyen en el comportamiento de los agentes, así como en la expansión tecnológica y financiera del sector. Esta línea de estudio ha incentivado el desarrollo de estudios teóricos y matemáticos.
En segundo lugar, se destaca el interés por pronosticar el comportamiento futuro de las variables macroeconómicas, sectoriales y macroclimáticas que determinan el comportamiento del precio de la energía. La incertidumbre que enfrentan el inversionista y el regulador del mercado determina su interés por desarrollar modelos que permitan identificar los momentos óptimos de inversión para generar valor a las firmas y minimizar los costos para el consumidor final.
Un tercer enfoque en los trabajos desarrollados consiste en la evaluación financiera y la valoración de los proyectos de estas características. Teniendo en cuenta el nivel de volatilidad de las variables que afectan la rentabilidad de este tipo de proyectos y las particularidades de cada uno de los casos de estudio, ha sido necesario buscar herramientas alternativas que incluyan la flexibilidad y la incertidumbre en la valoración.
Así se encuentran trabajos como:
La valoración tradicional de proyectos de inversión se ha caracterizado por la estimación de flujos de caja futuros (FC) que reflejan las expectativas del comportamiento de variables exógenas y endógenas –variables macroeconómicas y sectoriales–. Estos flujos se descuentan al costo de capital promedio ponderado (i), para ser comparados con los desembolsos requeridos al inicio (I) del proyecto, obteniéndose el valor presente neto (VPN) del proyecto. Este resultado permitirá determinar la aceptación o rechazo del proyecto, de tal manera que si el VPN es positivo será factible la ejecución del proyecto; de lo contrario, este se rechazará.

En los modelos convencionales de flujos de caja descontados (FCD), el efecto del riesgo está usualmente involucrado en la tasa de descuento (i). Esta tasa considera el costo de todas las fuentes de financiación de un proyecto, que se ajustan por el riesgo involucrado en este. La estructura del flujo de caja libre para realizar la valoración es:

Donde,
E: Utilidad operativa después de impuestos
φ: Depreciaciones
 : Cambio en capital de trabajo
: Cambio en capital de trabajo
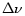 : Reposición en activos
fijos
: Reposición en activos
fijos
tax: Pago efectivo de impuestos.
La estimación de los flujos de caja requiere de información confiable que refleje el verdadero desempeño del proyecto. En el caso de un proyecto de energía térmica se requiere considerar un gran número de variables que generan múltiples incertidumbres. Por ello, es necesario modelar la volatilidad asociada a cada una de dichas variables, con el objetivo de estimar el valor del proyecto con un mayor ajuste. No obstante, aunque la utilización de la metodología del flujo de caja descontado es importante, no es suficiente para proyectos con este nivel de incertidumbre, y con la necesidad de tomar decisiones ante las trayectorias futuras del proyecto.
La teoría de opciones reales otorga a los directivos de las compañías flexibilidad respecto a la ejecución de proyectos, a la capitalización de nueva información y a las cambiantes condiciones del mercado, a fin de mejorar la oferta de servicios y el beneficio económico. El análisis de las opciones reales constituye una forma para determinar el valor de la flexibilidad implícita en cada proyecto y aprovecha positivamente la incertidumbre para aumentar el valor del proyecto. Al involucrar opciones reales en la valoración de un proyecto, se trata de estimar un valor presente neto expandido o modificado, el cual estaría conformado por dos componentes: el valor presente neto de los flujos de caja y el valor de la opción, lo que se conoce como un valor presente neto expandido [2].
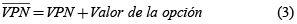
De acuerdo con las condiciones de cada proyecto se presentan varios tipos de opciones, tales como: abandonar, expandir, contraer, diferir, posponer, cerrar, opciones compuestas, entre otras (ver tabla 1). Estas opciones asumen flexibilidad en la toma de decisiones a futuro, lo que representa enfrentarse a cambios en el riesgo asumido y, por tanto, a variaciones en la tasa de descuento. En efecto los tomadores de decisiones se encuentran en condiciones de reaccionar ante las circunstancias cambiantes, y al hacerlo, afectan el comportamiento del flujo de efectivo.
El análisis de opciones reales es adecuado para la inversión en los activos de generación de energía eléctrica, ya que la inversión en dichos bienes es intensiva en capital y se caracteriza por ser en gran medida irreversible y generar costos hundidos. En consecuencia, la flexibilidad del proyecto tiene un impacto significativo en el valor de la inversión; adicionalmente en los últimos años los cambios climáticos han generado gran incertidumbre sobre la capacidad de generación a través de la riqueza hídrica; así, el carbón se ha convertido en una posibilidad de generación alternativa. La incertidumbre sobre los precios futuros del carbón introduce riesgos considerables en la toma de decisiones que afectan directamente el margen de utilidad esperada de proyectos de generación de energía, y por tanto, la capacidad instalada limitando la oferta.
El enfoque desarrollado en este campo mediante opciones reales ha sido amplio, debido principalmente a la gran cantidad de factores que influyen en las expectativas de los precios de la electricidad, lo que origina incertidumbre en el resultado financiero, y frena en muchos casos las inversiones. Esta relación ha sido siempre –conocida intuitivamente, pero con la introducción de la teoría de opciones reales, el analista tiene una herramienta para calcular y medir con más precisión el impacto que tiene la incertidumbre sobre el comportamiento de la inversión agregada [3]. Sin embargo, no existe un consenso sobre la metodología a utilizar para modelar la volatilidad lo que permite desarrollar investigaciones utilizando el Método Monte Carlo propuesto por Boyle [4] y el modelo utilizado por Cox-Ross-Rubistein [5], denominado generalmente modelo binomial. La metodología propuesta por Black-Scholes ha sido descartada por varios autores.
Para Kjærland, la discusión para seleccionar entre los dos modelos de valoración de opciones tiene su origen en las características especiales que posee la electricidad: por un lado, la tecnología actual no permite almacenarla, lo que implica que no pueda ser prestada, ni vendida en corto; no se puede comprar, ni devolverse más tarde. Esto viola los supuesto de la teoría tradicional de no arbitraje para la valoración de opciones [3]. Pero el supuesto de riesgo neutral no solo se está incumpliendo por las condiciones de la energía, sino también por las características del proyecto mismo, ya que se hace difícil encontrar un proyecto réplica en el que se puedan tomar posiciones cortas o largas, o incluso es difícil mantener el supuesto de que parte del proyecto que se está valorando o de sus opciones se pueda vender.
Para identificar el modelo que se debe seleccionar es necesario analizar los parámetros considerados en la valoración del proyecto, comparándolos con aquellos empleados para las opciones financieras.
• El precio del activo subyacente: en el caso de las opciones financieras es el precio del activo sobre el cual se plantea la opción, el cual es conocido por el inversionista en cada momento en el que evalúa su ejercicio. En contraste, en un proyecto de inversión este hace referencia al valor presente de los flujos de caja, los cuales no son conocidos por el inversionista, ya que no se tiene certeza sobre los resultados del proyecto en el futuro.
• El precio de ejercicio: es el precio que se debe pagar para ejercer una opción; es un parámetro que depende del tipo de opción a desarrollar, esto es, si es una opción de inversión, es el desembolso adicional para ampliar la planta y generar nuevos beneficios, y si se trata de una opción de desinversión, es el valor que se percibe por desinvertir en el proyecto. El comportamiento de este parámetro podría ser variable, o incluso, de comportamiento estocástico. Para el caso de las opciones financieras indica el precio al que el propietario de la opción puede ejercerla, y dicho valor es conocido a priori y permanece constante durante todo el tiempo del contrato.
• Tiempo hasta el vencimiento: tanto para la opción financiera como para la real es el plazo que dispone su propietario para ejercer la opción. En el caso de la opción financiera, el tiempo es definido en el contrato, mientras que en opciones reales depende del ciclo de vida del proyecto y es una variable definida por el analista.
• El riesgo: indica la volatilidad del activo subyacente. Para el caso de un proyecto de inversión en una planta térmica la incertidumbre depende del comportamiento de múltiples factores cuyo pronóstico es complejo, lo que conduce a una elevada exposición al riesgo. Algunos autores como Maya, Gallego y Hernández [6]; Lamothe [7] proponen las siguiente metodología para el cálculo de la volatilidad:
o Factor predominante: consiste en tomar la volatilidad del factor que le imprime un mayor nivel de riesgo al proyecto.
o Portafolio replica: consiste en tomar la volatilidad de un proyecto o una empresa con características similares.
o Simulación Monte Carlo: consiste en calcular la volatilidad de alguno de los parámetros de rentabilidad del proyecto, a partir del estudio estocástico de las variables y de la simulación Monte Carlo de los flujos de caja futuros.
Aunque las tres metodologías han sido utilizadas por diferentes autores, se comparten los argumentos planteados por Maya, Gallego y Hernández [6], donde se plantea que las dos primeras metodologías pueden sobrevalorar o subvalorar el riesgo del proyecto, en el caso del factor predominante al asumir una única variable de riesgo, y en el caso del portafolio réplica, al utilizar un proyecto diferente al que se está evaluando. Adicionalmente, se puede esgrimir este mismo argumento para utilizar Simulación Monte Carlo como metodología de valoración para un proyecto de energía, pues en lugar de calcular la volatilidad por este método y después utilizarla como un input en arboles binomiales, ya al realizar dicha simulación se tiene el comportamiento estocástico inherente al proyecto, y por lo tanto, se puede utilizar el mismo para valorar las opciones ante las posibles trayectorias futuras, sin correr el riesgo de mutilar alguna parte del comportamiento.
• Tasa de interés sin riesgo: en las opciones financieras refleja el valor temporal del dinero.
El hecho de que los flujos de caja de los proyectos de centrales de generación térmica tengan un comportamiento estocástico implica la necesidad de realizar la valoración a través de Simulación Monte Carlo, ya que uno de los supuestos del modelo binomial es que el precio del activo subyacente evoluciona según un proceso binomial multiplicativo.
Se han realizado aplicaciones atractivas de la planificación de las inversiones de generación de energía y el uso de opciones en operación de centrales eléctricas, empleando el ROA [8]. Estos desarrollos se deben principalmente al interés manifiesto de los gobiernos en el ámbito mundial por asegurar la prestación continua del servicio a la población y por las diferentes incertidumbres que dificultan su alcance. En la tabla 2 se presentan los aportes realizados por autores como: Kjærland [3], Kumbaro?lu, Madlener, & Demirel, [9], Fernandes, Cunha, & Ferreira [10], Boomsma, Meade, & Fleten, [11], Barria & Rudnick [12], Serati, Manera, & Plotegher [13], Madlener & Stoverink [8] quienes han abordado el estudio del mercado desde diferentes ángulos. Sin embargo, todos los trabajos manifiestan varios puntos en común: la necesidad de modelar el precio de la energía y las variables de incertidumbre en el mercado, la dificultad para estimar el costo de capital asociado a los proyectos, así como el interés por identificar los efectos de los cambios regulatorios en el precio [14].
En Colombia, la literatura relacionada con la aplicación de esta metodología en la valoración de proyectos es reciente y se ha aplicado desde diversos frentes. Mora, Agudelo y Dyner, (2004) proponen el empleo de la metodología de opciones reales para valorar un proyecto de inversión en generación de energía eólica en Colombia. Cayón y Sarmiento (2005) se concentran en el desarrollo de herramientas metodológicas de opciones reales y en el análisis de la información adicional con la que cuenta el inversionista al aplicar la primera y segunda derivadas del modelo de Black-Scholes, conocidas como delta y gamma. Maya, Hernández y Gallego [6] valoran un proyecto de energía eólica bajo ROA, donde su principal aporte es el estudio estocástico de las variables que lo afectan, para el cálculo de la volatilidad a través de simulación Monte Carlo.
2. DESCRIPCIÓN MODELO Y LAS VARIABLES
La evaluación de proyectos de generación de energía ha sido abordada desde varias perspectivas que van desde el diagnóstico hasta la valoración de los proyectos, por lo cual han permitido una amplia aplicación de diversas metodologías. Los directivos de las compañías generalmente tienen flexibilidad respecto a la ejecución de proyectos, la capitalización de nueva información y las cambiantes condiciones del mercado, a fin de mejorar la oferta de servicios y el beneficio económico. El análisis de las variables estocásticas constituye una forma para determinar el valor en cada proyecto.
2.1. Ingresos
Las variables explicativas que requiere la valoración de la opción real se concentran en la determinación de los ingresos y egresos que describen el proyecto. En este sentido, los ingresos se consideran determinados por la cantidad de energía producida y el precio de la energía. La cantidad se estima como la capacidad de generación de una planta térmica media en Colombia, cuyo combustible principal es carbón; en este caso se asume una capacidad de 150 MW. Para construir un modelo de proyección del precio de la energía, se asume que este se encuentra en función del clima y del mismo precio con rezagos de períodos anteriores, descrito por un modelo ARIMAX-GARCH (1,1). Como variable que mide el comportamiento del clima se analiza el indicador atmosférico denominado El Niño/Southern Oscillation (Enso).
Para introducir el Enso en el modelo se derivaron de este dos variables dummy, considerando que valores del índice inferiores a –0.5oC indicaba presencia de fenómeno de La Niña, mientras que valores superiores a 0.5oC indicaba presencia del fenómeno de El Niño, es decir, sequía. Para proyectar el comportamiento en el tiempo, se hizo la prueba de bondad de ajuste Kolmogorov-Smirnov (K-S) (ver figura 1) a la serie histórica mensual del Enso desde abril de 2004 a marzo de 2012, como resultado se obtuvo una distribución normal con la siguiente media y desviación estándar: Enso N (–0.177083, 0.775477). Para el modelo proyectado se incluyen las correlacciones históricas existentes entre el resultado del Enso de un mes y los meses subsiguientes, de esta forma se evita que el modelo genere datos atípicos entre los meses.
La matriz de correlaciones indica que a medida que el diferencial de tiempo se incrementa (Δtiempo = T – t), la presencia de invierno o verano en el período t tiene una relación lineal que disminuye, e incluso presenta un comportamiento inverso en T.
Dado que para el comportamiento del precio de la energía no se obtuvo ajuste en la distribución normal, y teniendo en cuenta estudios de algunos autores como Gil y Maya [15], Villada, et al [16], entre otros, que concluyen que el precio de la energía no tiene volatilidad constate, se busca un a ARIMA-GARCH para la media y la varianza, respectivamente. A continuación se presentan tres de los modelos analizados (tabla 3).
En el modelo el precio actual tendrá crecimiento de 18 veces en el período en el que hay presencia de sequía, con respecto al precio del período anterior. Sin embargo, la presencia de sequía en un período determinado descuenta el efecto sobre el precio, dado que se presentó una temporada de lluvias tres períodos antes y el fenómeno de sequía había iniciado desde el período anterior.
2.2. Egreso por combustible: pronóstico de los precios de carbón
Uno de los principales determinantes en la valoración de proyectos de generación de energía es el costo del combustible empleado en la operación. Para el presente análisis se considera el carbón como principal combustible, por lo que es necesario modelar el precio de este insumo. La información que se empleó en esta estimación es el precio FOB de exportaciones mensual expresado en Us$/Ton publicado por la UPME.
El modelo de mayor ajuste es un GARCH (1,1), el cual sugiere que la rentabilidad sobre el precio del carbón para el período analizado depende de su comportamiento en los dos últimos meses, así como de la presencia de El Niño en el período (tabla 4).
La cantidad de carbón necesaria para la generación de una planta media se considera de 715.962 toneladas anuales.
2.2.1. Otros egresos
El estudio contiene los costos y gastos operativos considerados para una empresa de generación térmica con una capacidad de producción de 150 MW. Las erogaciones adicionales al carbón para una planta de estas características son tomados de la UPME [17], las cuales estaban en dólares a valores del año 2005, por lo que se actualizaron con la inflación de Estados Unidos para el año 2011 y se convirtieron a pesos con la tasa de cambio de diciembre de ese año.
Asimismo, las inversiones consideradas se tomaron del informe realizado por la UPME (2005) [17]. Para estimar los gastos se siguió la misma metodología empleada en la proyección de los costos. En la tabla 5 se muestra el tipo de inversiones para una planta de producción de 150 MW a valores en dólares de 2005, y la conversión a valores en dólares y pesos de 2011.
Estos datos sirven como input para el modelo de valoración realizado con el método de flujo de caja libre, sin tener en cuenta endeudamiento.
Para la elaboración de flujo de caja se asume que el proyecto demorará dos años en la construcción y luego se hacen proyecciones a 10 años del estado de resultados y del flujo de caja libre. La depreciación de las inversiones se toma al mismo plazo de proyección; el flujo de pago de impuestos tiene en cuenta los momentos de desembolso y los anticipos necesarios. Para el capital de trabajo se asumen 5 días de efectivo requerido para la operación sobre las ventas, 34 días de cartera, 25 días de inventarios sobre las compras de carbón y 35 días de proveedores sobre el pago del carbón y otros insumos para la producción. El capex se dividió en un 50% para cada uno de los dos años de ejecución de la obra.
Se estima el valor terminal con la metodología del valor en liquidación del proyecto, calculando la recuperación del capital de trabajo y el pago de impuestos para el año 11 de proyecciones. El costo de capital se hace partiendo de la teoría del CAPM [18], desde la perspectiva de un inversionista internacional invirtiendo en Colombia. Para la tasa libre de riesgo se utilizaron los bonos del tesoro de Estados Unidos a 10 años, calculando el promedio de la rentabilidad anual desde enero del año 2009 hasta diciembre del año 2010; la serie fue tomada con una periodicidad mensual. Para el Beta del sector se toma el calculado por Damodaran [19] del sector energía en mercados emergentes. Como rentabilidad esperada del mercado se hizo el cálculo del promedio de las variaciones porcentuales mensuales de S&P500 desde enero de 2009 hasta diciembre 2011 y luego la tasa encontrada se convierte a efectiva anual. Como devaluación futura se toma la proyección del dólar siguiendo el modelo econométrico construido para la divisa, mostrado anteriormente.
3. ALTERNATIVAS DE INVERSIÓN EN EL PROYECTO
Una vez modeladas todas esta variables en Excel y bajo el programa @RisK se hace una simulación con 10.000 iteraciones y se pone como variable de salida el VPN del proyecto (Ver figura 2).
Los resultados del VPN indican una gran variabilidad y ancho en las posibles trayectorias. El VPN promedio es de –181.000 millones de pesos y el 90% de los resultados se encuentran entre –1 billón y +1 billón de pesos colombianos. Los resultados de la valoración son poco satisfactorios, desde el punto de vista financiero, debido a: la variabilidad de los posibles resultados, la tendencia a que los mismos sean negativos, la alta probabilidad de que el VPN sea negativo y los múltiples escenarios que no son satisfactorios bajo el criterio del VPN.
Teniendo en cuenta los grandes niveles de inversión en este tipo de proyectos, se plantean tres opciones reales en la construcción de un proyecto de estas características. La primera opción consiste en la posibilidad de continuar a los 10 años de operación. Según la UPME [17], una planta de estas características puede tener una duración de 20 años en la generación de ingresos. No obstante, el proyecto se valoró dejando como valor terminal el valor de liquidación, dado que utilizar otra metodología sería introducir un mayor riesgo al mismo, pues si bien en algunas de las trayectorias del proyecto el valor terminal sería positivo, en otras se podría hacer bastante negativo, dadas las condiciones de volatilidad del precio de la energía y del precio del carbón. Por esta razón se opta por deja el valor terminal como una opción real existente, donde si el valor presente de los flujos de caja del año 11 al año 20 es positivo, entonces se continuará con el proyecto; de lo contrario, se liquida el proyecto (ecuación 5)
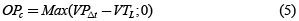
Donde:
OPc: Valor de la opción de continuar a los 10 años.
VPΔt: Valor presente de los flujos de caja del año 11 al año 20.
VTL: Valor terminal calculado por el método de valor en liquidación.
Δt: Período de proyección
Esta oportunidad es semejante a una opción financiera de compra de tipo europeo, donde solo existe una fecha posible de ejercicio, con la flexibilidad de continuar o no continuar el proyecto después del año 10. Esto sólo se dará cuando los resultados del año 11 hasta el año 20 sean satisfactorios; de lo contrario, se preferirá dejar el proyecto, asumiendo que se recupera el capital de trabajo como valor en liquidación, y bajo el supuesto de que el valor de recuperación de los activos fijos es solo suficiente para pagar su desmantelamiento.
La flexibilidad de tomar la continuación del proyecto como una opción genera un valor incremental entre cero y 5,7 billones de pesos, con un valor medio de 520.000 millones de pesos. El VPN del proyecto, contemplando la opción de continuar, traslada la media de-181.000 millones a 346.800 millones de pesos, evidenciando el impacto positivo de valorar la flexibilidad; sin embargo los valores mínimos posibles, y la probabilidad de que el VPN sea menor a cero siguen haciendo del proyecto, un resultado financiero no satisfactorio.
La segunda opción que se evalúa es la de abandonar el proyecto, que consiste en dimitir al proyecto y a sus flujos de caja futuros, cuando exista la posibilidad de que los mismos sean reiteradamente negativos, en aquellas trayectorias donde el margen generado por el precio de la energía y del precio del carbón es insuficiente para solventar los costos de funcionamiento y de inversión en la planta. En estos casos existe esta opción estratégica en el proyecto, pues no tiene sentido incurrir en pérdidas repetitivas. La opción de abandono tiene valor cuando el valor presente de los flujos de caja es negativo, como se indica en la ecuación 6.

Donde:
OPA: Valor de la opción de abandono.
VPx–10: Valor presente de los flujos de caja desde cualquiera año hasta el año 10.
Para cada una de las trayectorias posibles y en cada uno de los años se evalúa el valor presente de los flujos hasta el año 10 de la siguiente forma:

Donde x es el año desde al cual una trayectoria hace que el VP del proyecto sea totalmente negativo, fci son los flujos de caja de dicha trayectoria y se traen a valor presente con la tasa de descuento. Es así como se evalúa para todas las trayectorias posibles. Adicionalmente, se supone en este caso que el valor de recuperación de activos, como el terreno o la planta, cubre los gastos de liquidación del mismo.
Esta es una opción que se puede asemejar a una opción financiera de venta de tipo americano; sin embargo, en el mundo de las finanzas corporativas es difícil asumir que las decisiones se toman en tiempo continuo; por lo tanto, se podría asemejar a una opción de tipo bermuda, donde las decisiones y las trayectorias se evalúan al final de cada uno de los años de forma discreta.
La opción de abandono genera un valor agregado para el proyecto entre cero y 2,5 billones de pesos con un valor esperado de 494.000 millones de pesos. El resultado del VPN del proyecto teniendo en cuenta la opción de abandono, oscila entre –1 billón de pesos y 4 billones de pesos y la media es de 313.200 millones de pesos (ver figura 4). Ahora bien, el aporte fundamental de tener en cuenta la opción de abandono consiste en considerar la posibilidad de eliminar estratégicamente muchas de las trayectorias negativas que toma el proyecto en el tiempo. En el gráfico se observa cómo el 90% del VPN toma valores entre –430.000 millones de pesos y 1.32 billones de pesos, que comparados con los resultados iniciales, disminuyen el riesgo y la probabilidad de que el VPN tome valores menores a cero, por lo tanto, se reduce la posibilidad de destruir valor. Quizás uno de los aportes fundamentales de la opción de abandono es aumentar el valor del proyecto, a través de la flexibilidad de poder tomar decisiones estratégicas que dejan de impactar negativamente el proyecto, situación que no se evidencia cuando se evalúa el proyecto de forma determinística. Existen otros casos donde la opción de abandono le genera explícitamente valor al proyecto, y hay un valor de salvamento o de venta de los activos del mismo, pero no es interés de este trabajo abordar dicha alternativa.
La tercera opción consiste en ampliar el proyecto en un 50%, dada la existencia de economías de escala y el no tener que hacer nuevamente algunas de las inversiones. Esta opción existe siempre que el margen generado por el precio de la energía y el costo del carbón sea suficiente para que el valor presente de los flujos de caja incrementales sea superior a la inversión adicional requerida. El valor de la opción está expresado en la ecuación 7:
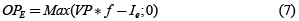
Donde:
OPE: Valor de la opción de expansión.
VP: Valor presente de los flujos del proyecto.
f: Factor porcentual de expansión.
Ie: Inversión incremental asociada a la expansión.
Una de las características de la opción de expansión, a diferencia de la opción de crecimiento, es que la misma depende de los flujos de caja del proyecto convirtiéndose el VP en el subyacente. En este caso al ejercer la opción de expansión en un porcentaje, se generan ingresos y beneficios adicionales en dicho porcentaje y se aumenta el VP en la proporción de la expansión. Para este caso en concreto se asume una expansión del 50% de los beneficios, para un lapso de tiempo de 10 años, equivalente al tiempo considerado en la inversión inicial. De igual manera, se asume que la inversión asociada a la expansión representa el 50% de las inversiones que se deben repetir, ajustadas por inflación para cada uno de los años (ver tabla 6).
Un argumento para no asumir la expansión del proyecto en un porcentaje mayor es el límite existente de las economías de escala; si se quisiera hacer una expansión mayor es posible que se deban hacer inversiones adicionales en vías de acceso, predios, etc. Adicionalmente, se asume que una inversión adicional del 50% y, por lo tanto, un incremento de la capacidad instalada y de la posibilidad de generar energía en 75 MW, no genera impacto en el mercado de la energía. Los resultados de la opción de expansión se presentan a continuación:
Similar a la opción de continuar, la opción de expansión le genera un mayor valor al proyecto pero no disminuye el riesgo de que el proyecto tome valores extremos. La opción de expansión puede tomar un valor entre cero y 38 billones de pesos, con un valor medio de 3,8 billones de pesos. El VPN del proyecto, contemplando la opción de continuar, traslada la media de-181.000 millones a 3,6 billones de pesos, que muestra la importancia de tener en cuenta esta opción; es evidente el valor adicional que le genera la opción de expansión al proyecto. Sin embargo, este valor se presenta en las trayectorias donde los márgenes del proyecto se hacen importantes, dado un precio de la energía alto y un precio del carbón lo suficiente por debajo para generar rentabilidad. Pero con esta opción poco puede hacer en las trayectorias negativas del proyecto, pues ante los escenarios muy rentables se puede tomar la decisión de ampliar y ganar más dinero, pero ante las pérdidas esta opción genera efecto nulo.
4. CONCLUSIÓN
La restructuración del mercado de electricidad en Colombia ha incentivado la inversión en nuevos proyectos de generación de energía. La utilización de la valoración de éstos a través de flujo de caja descontado se asocia a un análisis estático que no considera el comportamiento estocástico de las variables que lo determinan. Esta omisión puede generar una sobrevaloración o subvaloración de los proyectos, afectando la exposición del riesgo y los beneficios esperados de los inversionistas. El desconocimiento del valor económico futuro de los proyectos de generación energética incentiva el estudio sobre las variables que determinan sus resultados, proporcionando a los inversionistas indicios sobre las alternativas que pueden aprovechar, en diferentes escenarios.
Este trabajo incorpora la modelación de la volatilidad estocástica de variables exógenas que consideran la incertidumbre en la decisión de inversión. Para ello, se emplearon como herramientas modelos ARIMA-GARCH. Los resultados sugieren que el modelo de mayor ajuste, para el caso de los retornos sobre el precio de mercado de la energía, es un ARIMAX-GARCH (1,0), donde el fenómeno de sequía de los tres meses anteriores implica un incremento porcentual sobre el precio de este commodity; intuitivamente, se pude afirmar que dicho resultado se debe a la disminución de los caudales ocasionada por los comportamientos extremos del clima, los cuales requieren tiempo para contar con los niveles óptimos.
El comportamiento del clima, según el pronóstico del Enso, se modelo mediante Monte Carlo, el cual se reconoce como un método de simulación numérica que suele utilizar para simular un conjunto muy grande de procesos estocásticos. Para las condiciones analizadas la simulación indica una probabilidad del 19% de presencia de sequía extrema, que es el contexto requerido para optimizar la producción de las generadoras térmicas.
La modelación de la volatilidad de las diferentes variables exógenas se considera como insumo para valorar el proyecto a través de flujo de caja descontado. Sin embargo, los resultados recomiendan la no ejecución de este, debido principalmente al crecimiento de los costos, explicado por el incremento exponencial del precio del carbón. Estos resultados sugieren la necesidad de implementar herramientas complementarias que involucren diferentes escenarios. El análisis de opciones reales es una herramienta que permite valorar la flexibilidad de los proyectos de inversión ampliando el margen de estrategia de los tomadores de decisiones. En este caso se contrastan los resultados obtenidos a través de la metodología de flujo de caja descontado y de opciones reales para valorar una planta térmica con capacidad de generación de 150 MW.
La existencia de proyectos con variables estocásticas que tienen cambios continuos y periódicos en pequeñas fracciones de tiempo origina la posibilidad y la existencia de una opción de cierre temporal. En este contexto existe la posibilidad de realizar trabajos que contribuyan al desarrollo teórico y la valoración de este tipo de opciones. También es de gran importancia considerar en futuros trabajos la influencia de las restricciones e incentivos que concede el gobierno en la negociación de proyectos de energía.
REFERENCIAS
[1] M. d. M. y. E. Minminas, ''Sector Energía Eléctrica,'' ed. Bogotá: Ministerio de Minas y Energía, 2011.
[2] L. Trigeorgis, Real Options: Managerial Flexibility and Strategy in Resource Allocation. United States of America: Asco Trade Typesetting Ltd, 1999.
[3] F. Kjærland, ''A real option analysis of investments in hydropower–The case of Norway,'' Energy Policy, vol. 35, pp. 5901-5908, 2007.
[4] P. P. Boyle, ''Options: A Monte Carlo approach,'' Journal of Financial Economics, vol. 4, pp. 323-338, 1977.
[5] J. C. Cox, et al., ''Option pricing: A simplified approach,'' Journal of Financial Economics, vol. 7, pp. 229-263, 1979.
[6] C. Maya, et al., ''La valoración de proyectos de energía eólica en Colombia bajo el enfoque de opciones reales,'' Cuadernos de Administración 2012.
[7] P. Lamothe, Opciones financieras y productos estructurados MADRID MCGRAW HILL, 2006.
[8] R. Madlener and S. Stoverink, ''Power plant investments in the Turkish electricity sector: A real options approach taking into account market liberalization,'' Applied Energy, vol. 97, pp. 124-134, 2012.
[9] G. Kumbaroglu, et al., ''A real options evaluation model for the diffusion prospects of new renewable power generation technologies,'' Energy Economics, vol. 30, pp. 1882-1908, 2008.
[10] B. Fernandes, et al., ''The use of real options approach in energy sector investments,'' Renewable and Sustainable Energy Reviews, vol. 15, pp. 4491-4497, 2011.
[11] T. K. Boomsma, et al., ''Renewable energy investments under different support schemes: A real options approach,'' European Journal of Operational Research, vol. 220, pp. 225-237, 2012.
[12] C. Barria and H. Rudnick, ''Investment under Uncertainty in Power Generation: Integrated Electricity Prices Modeling and Real Options Approach,'' IEEE Latin America Transactions, 2011.
[13] M. Serati, et al., ''Modelling electricity prices: from the state of the art to a draft of a new proposal,'' LIUC Papers in Economics, 2008.
[14] M. A. A. Arango, ''Modelo para determinar una canasta hidro-térmica óptima en proyectos de inversión en el mercado de generación de energía, bajo condiciones de incertidumbre,'' Doctorado, Universidad Nacional de Colombia, Medellín, 2012.
[15] M. M. Gil Zapata and C. Maya Ochoa, ''Modelación de la volatilidad de los precios de la energía eléctrica en Colombia,'' Revista Ingenierías Universidad de Medellín, vol. 7, pp. 87-114, 2008.
[16] F. Villada, et al., ''Pronóstico del Precio de la Energía Eléctrica usando Redes Neuro-Difusas,'' Información tecnológica, vol. 22, pp. 111-120, 2011.
[17] U. M. e. d. C. UPME, ''Costos indicativos de generación eléctrica en Colombia,'' ed. Bogotá: Unidad Minero energética de Colombia UPME, 2005.
[18] T. E. Copeland, et al., Financial Theory and Corporate Policy 4ed.: Pearson Addison Wesley, 2005.
[19] A. Damodaran. (2012). Betas by Sector. Available: http://pages.stern.nyu.edu/~adamodar/