ARTÍCULOS

MODELOS CINÉTICOS DE DEGRADACIÓN TÉRMICA DE POLÍMEROS: UNA REVISIÓN

KINETIC MODELS OF POLYMER THERMAL DECOMPOSITION: A REVIEW

Laura María Aranzazu Ríos^*; Paula Victoria Cárdenas Muñoz^*; Juan Manuel Cárdenas Giraldo^*; Guillermo Humberto Gaviria^*; Andrés Felipe Rojas González^**; Javier Ignacio Carrero Mantilla^**

^** Ph.D. Profesores Asociados. Departamento de Ingeniería Química, Grupo GIAR. Universidad Nacional de Colombia, sede Manizales (Cra. 27 # 64 – 60). Teléfono: (+57+6) 8879300 ext. 50352. E-mail, anfrojasgo@unal.edu.co, jicarrerom@unal.edu.co

Recibido: 26/11/2012
Aceptado: 25/10/2013

RESUMEN

Esta revisión se dedica al ajuste de parámetros para modelos cinéticos de degradación térmica de polímeros usando termogravimetría. Primero se describen los fundamentos del análisis de datos y se resumen las ecuaciones básicas. Luego los modelos cinéticos se clasifican según estas categorías: isotérmicos, diferenciales, integrales, e isoconversionales. Las aproximaciones para la integral de Arrhenius se presentan en una sección aparte. Por último se da un esquema de clasificación para elegir el método de análisis de datos y se muestran algunas expresiones nuevas, desarrolladas a partir de aproximaciones de la integral de Arrhenius.

PALABRAS CLAVE

Cinética, polímeros, degradación térmica, integral de Arrhenius

ABSTRACT

This review is focused on the adjustment of parameters for kinetic models of polymer thermal decomposition by using thermogravimetry. First, fundamentals of data analysis are described and basic equations are summarized. Then, kinetic models are classified according to the following categories: isothermal, differential, integral, and isoconversional. Approaches to the Arrhenius integral are shown in a separate section. Finally, a classification scheme is provided in order to choose the data analysis method and some new expressions developed from approaches to the Arrhenius integral are depicted.

KEY WORDS

Kinetics; polymers; thermal decomposition; Arrhenius integral.

INTRODUCCIÓN

La predicción de la estabilidad de los materiales poliméricos es de gran utilidad práctica, y requiere establecer su cinética de degradación térmica. En los estudios cinéticos se emplean técnicas de análisis térmico, ensayo mecánico, y cromatografía. En el análisis térmico una propiedad física de una sustancia, o de sus productos de reacción, se mide como una función de la temperatura. Dentro de esta categoría la termogravimetría (TG por sus siglas en inglés) y la calorimetría diferencial de barrido (DSC) se usan para determinar parámetros cinéticos [1].

La TG es muy utilizada para estudiar la cinética global o macroscópica de la degradación térmica de polímeros porque de sus resultados se pueden obtener los parámetros cinéticos [2, 3]. Hay dos tipos de termogravimetría: el análisis termogravimétrico (TGA) y la termogravimetría diferencial (DTG). En el TGA se mide la masa de la muestra o el porcentaje remanente durante su calentamiento en condiciones controladas, mientras que en la DTG se mide la velocidad de pérdida de masa. Los resultados en función del tiempo o la temperatura representan el perfil termogravimétrico de un material [4]. Tanto en TGA como en DTG el tipo de calentamiento define la termogravimetría y los principales tipos son [4, 5]:

• Isotérmica: temperatura constante.

• Cuasi-isotérmica: la muestra se calienta hasta masa constante en cada uno de una serie de incrementos de temperatura.

• No isotérmica, o dinámica: la temperatura cambia de una manera predeterminada, preferiblemente lineal (velocidad de calentamiento constante).

La termogravimetría isotérmica presenta estas ventajas [6]: i) permite detectar cambios de orden y mecanismo de reacción; ii) la velocidad de descomposición se obtiene resolviendo analíticamente una ecuación diferencial o integral, permitiendo una evaluación fácil de parámetros; y iii) evita gradientes de temperatura en la muestra debidos a la conducción de calor no estacionario. Pero también tiene limitaciones [7]: i) puede llegarse a una conversión considerable sin alcanzar la temperatura predefinida del análisis; ii) no permite conocer la temperatura de inicio de la reacción; iii) requiere varios experimentos a diferentes temperaturas, por lo que, iv) necesita cantidades considerables de muestra, además de trabajo tedioso y largo tiempo; y v) la temperatura se puede alejar del valor especificado debido a reacciones exotérmicas o endotérmicas, invalidando los datos.

De otro lado, la termogravimetría no isotérmica es más precisa para determinar los parámetros cinéticos y resuelve las limitaciones del método isotérmico. Tiene otras ventajas [7]: i) uso de pequeñas cantidades de muestra, ii) facilidad y rapidez del análisis, iii) mayor reproducibilidad debido al gran número de datos obtenibles en un solo experimento, iv) eliminación del error inducido por el periodo de inducción térmico, v) permite barrer en forma rápida un amplio rango de temperaturas, y vi) permite estudiar la influencia de la velocidad de calentamiento.

La elección de un tipo de análisis para determinar la cinética de degradación depende del tipo de material. Existen al menos 52 métodos analíticos distintos [8-12], que se han aplicado en degradación térmica [10], pirólisis [13], y combustión [5]. Por tipo de material hay métodos publicados para termoplásticos [10-11, 14-15], elastómeros [16], materiales compuestos y nonocompuestos [12], mezclas de polímeros [17], biopolímeros [18], carbón [5], residuos de petróleo [19], cauchos [20], pino [21], celulosa [6], quitina y quitosano [22], resinas epóxicas [23], fibras naturales-biomasa [24], aceites vegetales [7], y biodiesel [9].

Sin embargo, hay un punto común y es que cualquiera que sea el tipo de análisis, el propósito del tratamiento matemático de datos TG es obtener el ''triplete cinético'': energía de activación, orden de reacción, y factor preexponencial (llamado también factor de frecuencia). El objetivo de este trabajo es clasificar y resumir las aproximaciones y modelos matemáticos empleados para calcular el triplete cinético en la degradación térmica de polímeros. De esta forma, el experimentador tiene un esquema que le permite elegir la forma en que procesará los datos. También se presentan algunos modelos nuevos, obtenidos a partir de aproximaciones encontradas en la literatura.

1. ASPECTOS COMUNES DEL TRATAMIENTO DE DATOS EXPERIMENTALES

La termogravimetría se basa en la medición de la masa de muestra en función del tiempo durante el calentamiento. Pero en lugar de la masa los cálculos se basan en la fracción de pérdida de peso, o conversión, definida como:

donde w₀, w_t, y w_∞ son, respectivamente, las medidas de masa en el inicio, en el tiempo t, y al finalizar el análisis. Los valores de α quedan en el intervalo [0,1] . La variable dependiente puede ser una función de α, dα/dt, o ambas. La variación dα/dt se mide experimentalmente (DTG) o se calculada a partir de datos α vs. t (TGA). En termogravimetría no isotérmica se usa la variación respecto a la temperatura, dα/dT. Sin embargo, dα/dt y dα/dT están relacionadas por la velocidad de calentamiento B:

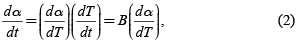
así, con B se puede obtener dα/dt de datos no isotérmicos. Y usar varios valores de B reduce los efectos limitadores de la transferencia de calor.

La variación dα/dt se toma como el producto de dos funciones, una de T y otra de α

La constante de velocidad k(T) sigue la ecuación de Arrhenius,

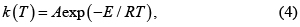
donde E es la energía de activación (o de ''activación aparente''), A es el factor preexponencial, y R=8.31451J/mol·K. La función f(α) depende del orden de reacción n. Por ejemplo, para un modelo de ley de potencia [7]

pero existen otras formas de f [25, 13]. El triplete cinético A, E, n es el conjunto de parámetros que gobierna la Ec. (3) y se obtiene de los datos experimentales dα/dt, T, y α en las formas que se describen en las siguientes secciones.

2. CLASIFICACIÓN

El criterio de mayor uso divide a los modelos en diferenciales e integrales según su variable dependiente [7, 22]. En los modelos diferenciales se ajustan datos de dα/dt en función de T y α. Por ejemplo, empleando la forma lineal de la Ec. (3),

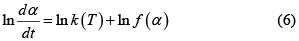
se puede obtener el orden de reacción y luego los parámetros A y E. Para obtener la ley cinética y el mecanismo de reacción de la degradación térmica de polímeros se consideran preferibles los modelos diferenciales que los integrales [25]. Sin embargo hay excepciones, por ejemplo el modelo Freeman-Carroll (ver tabla 3) no permite discernir el mecanismo de reacción dado que produce siempre un orden de reacción aparente [27].

Los modelos integrales usan datos de α, o una integral de α, en función de t o T. Por ejemplo, al emplear la Ec. 5 la forma integral de α es

de esta forma en un análisis isotérmico los parámetros de Arrhenius (A, E) se pueden obtener de datos de t en función de 1/T. No son aplicables a muy bajos o muy altos grados de conversión [22].

También existen categorías definidas por el tipo de velocidad de calentamiento: inicial, o cíclica. Y modelos diferenciales-diferenciales, que emplean diferencias entre dα/dt [26]. Una clasificación general es la de modelos de ajuste frente a modelos libres [26]. La categoría de ajuste incluye todos los modelos con una forma de f(α) asumido de antemano. En cambio, en los modelos libres no es necesario definir la función f(α).

En los métodos libres isoconversionales, del conjunto total se seleccionan datos con el mismo valor α, aunque a distintas temperaturas o velocidades de calentamiento. De esta manera f(α) se vuelve constante, y los parámetros A y E son independientes de la forma de f. Por ejemplo, en la Ec. 6 dα/dt depende solo de la temperatura, a través de la constante de reacción k(T). Sin embargo, el tratamiento isoconversional se puede aplicar sin importar si los datos son TGA (α) o DTG (dα/dt).

De los resultados de E obtenidos en los métodos isoconversionales se puede deducir el tipo de cinética; si con distintos α se obtiene prácticamente el mismo E la cinética es simple de un solo paso; de lo contrario, es de varias etapas [28]. Sin embargo, también tienen desventajas; para empezar, necesitan muchas mediciones a diferentes B para obtener suficientes datos a cada valor de α [6]. Además, en modelos integrales están limitados a valores de E relativamente altos y son propensos a la acumulación de errores. Esto se debe a condiciones de frontera con frecuencia mal definidas y a los métodos de aproximación utilizados en las integrales.

3. MÉTODO DIFERENCIAL FRENTE A MÉTODO INTEGRAL

En análisis isotérmico se puede aplicar el método diferencial porque se obtienen datos de α y dα/dt a diferentes valores fijos de temperatura. Por ejemplo, de la Ec. 6, con f(α)=(1–α)ⁿ

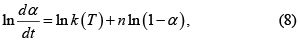
y para cada temperatura la gráfica ln(dα/dt) frente a ln(1–α) proporciona el orden de reacción n de la pendiente, y k(T) del intercepto. Luego al usar la forma lineal de la ecuación (4)

los parámetros A y E se obtienen del intercepto y la pendiente de la gráfica lnk(T) frente a 1/T. El método integral se basa en la Ec. 3, por ejemplo con f(α)=(1–α)ⁿ

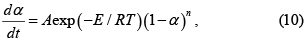
y al integrar se obtiene

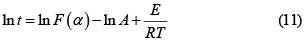
donde F(α) está definido en la Ec. 7. En forma similar al caso diferencial el parámetro E se obtiene de la pendiente de la gráfica ln t frente a 1/T.

Con datos no isotérmicos el análisis integral se basa en la velocidad de calentamiento definida en la Ec. 2. Remplazando dα/dT=(1/B)(dα/dt) en las Ecs. 3-4 se obtiene

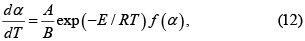
que se integra desde la temperatura de arranque (T = T₀ para α = 0) y la temperatura final (T = T para α = α)

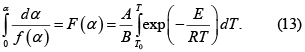
Si las temperaturas del proceso son mucho mayores que la temperatura inicial se acostumbra hacer T₀ = 0 en la integral del lado derecho [1]

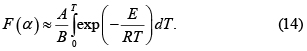
4. APROXIMACIONES PARA LA INTEGRAL DE ARRHENIUS

El término 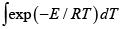es la ''temperatura integral'' o ''integral de Arrhenius''. Cuando el calentamiento es hiperbólico, es decir T = (a – Bt)^–1 la integral tiene solución analítica y la Ec. 14 es [30]

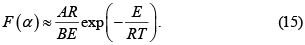
Aunque en el caso general solo queda estimar la integral de Arrhenius con métodos numéricos de cuadratura su valor se puede aproximar si se reescribe en términos de la variable x = E / RT [29]. De esta forma

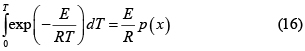
donde

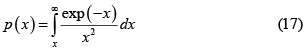
Así por ejemplo la Ec. 14 se reduce a

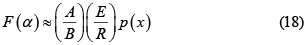
Al igual que la forma original, la integral p(x) no se puede evaluar analíticamente [2], y además, su límite superior es indeterminado. Sin embargo, el cambio de variable T → x es útil porque la forma de p(x) la hace similar a las funciones especiales Γ(x) y erf(x) (función error).

Se han publicado cientos de aproximaciones para p(x) [29, 32-33], que en su mayoría siguen la expresión [34-35]

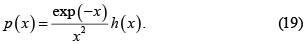
La aproximación es de tipo exponencial si h(x) tiene la forma [36]

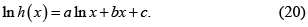
Pero también se les llama exponenciales a las formas análogas para p(x),

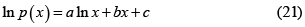
o

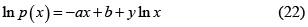
(en estas expresiones los parámetros a y b no pueden ser ambos cero). En la tabla 1 se presentan algunas aproximaciones exponenciales, y en las referencias [29, 36] se dan varios ejemplos de la forma de la Ec. 22 incluyendo los parámetros a, b, y y.

Las aproximaciones racionales vienen de la integración por partes p(x) = e^–x/x–E₁(x) y de la expansión en fracciones continuadas de la función integral E₁(x) [32, 37]. Se les llama racionales porque h(x) es el cociente de dos polinomios [37]

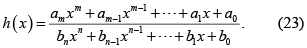
En la tabla 2 se dan varios ejemplos en forma lineal de aproximaciones racionales.

La precisión y exactitud de las aproximaciones exponenciales y racionales han sido revisadas a fondo [29, 32-33, 35]. Para un mismo conjunto de datos, distintas aproximaciones de p(x) pueden producir resultados de A y E diferentes [3]. En las propuestas más recientes no se ha notado una mejora y los resultados obtenidos con las expresiones de las referencias [34, 37] siguen siendo aceptables, en particular el cociente de dos polinomios de grado 4 se considera de gran exactitud [33].

5. ELECCIÓN DE MODELOS Y MÉTODOS

El análisis de datos requiere elegir una forma de f(α) y la manera de calcular los parámetros A y E. Existen numerosas formas de f(α) reportadas en la literatura [13, 25]. Para el caso particular de degradación térmica de polímeros, se recomienda la forma de ley potencia f(α) = (1–α)ⁿ, Ec. 5 [9, 17, 24, 38-39].

De otro lado, hay tres criterios clave para elegir el método de cálculo de los parámetros de Arrhenius:

• Si los datos son isotérmicos o no.

• El tipo de datos disponible: α o dα/dt Para el caso, de un conjunto de datos α(t) se puede calcular dα/dt en forma numérica.

• Si hay series de datos a diferentes velocidades de calentamiento. Esto permite hacer un análisis isoconversional.

En la figura 1 se muestra un esquema de clasificación basado en los criterios anteriores. Para datos isotérmicos el análisis puede ser integral (con α) o diferencial (con dα/dt). Esas dos opciones se pueden usar también para datos no isotérmicos, pero con estos el análisis puede ser isoconversional o no.

Además del esquema de clasificación se presenta un resumen de modelos reportados en la literatura para el estudio cinético de la degradación térmica de polímeros (tablas 3 y 4). Son variaciones de las ecuaciones 8 y 11, en las que se pueden aplicar aproximaciones exponenciales o racionales para p(x). Los modelos están clasificados en no isoconversionales (tabla 3) e isoconversionales (tabla 4). En la tabla 3 los modelos Diferencial de Arrhenius, Kissinger, Flynn-Wall, Chang y Dinámico son modelos diferenciales; el modelo Freeman-Carroll es diferencial-diferencia; los demás modelos son integrales. En la tabla 4 los modelos de Friedman, Sharp y Friedman-Reich-Levi son diferenciales, mientras que los demás son modelos integrales.

Las formas de los modelos reportados en la tabla 4 con un asterisco, 12 en total, fueron desarrollados en este trabajo a partir de aproximaciones de p(x) descritas por Deng [29]. Por ejemplo, la aproximación de Cai-He

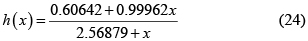
se remplazó en la Ec. 19

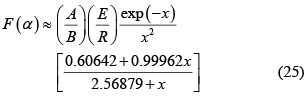
y con la definición x = E / RT se obtuvo la forma lineal

El mismo procedimiento se aplicó para todas las otras formas mencionadas.

6 CONCLUSIONES

Al reducir la clasificación de los modelos para analizar datos termogravimétricos a cuatro categorías (isotérmicos, diferenciales, integrales, e isoconversionales) siempre es posible elegir un método para obtener el triplete cinético. En particular los métodos isoconversionales requieren más datos experimentales, pero se basan en el mismo conjunto de ecuaciones que los demás.

Como la mayoría de los métodos para calcular los valores de los parámetros cinéticos se basa en formas lineales, el uso de aproximaciones para la integral de Arrhenius facilita el ajuste de datos al remplazar la integral por una función. De esa forma se pueden obtener nuevas expresiones, tal como se mostró en este trabajo.

En cuanto a las aproximaciones, se establece que las aproximaciones racionales son utilizadas en métodos analíticos de modelos de ajuste y modelos libres, mientras que las aproximaciones exponenciales son específicamente aplicables en modelos de métodos libres, especialmente en métodos isoconversionales.

AGRADECIMIENTOS

A la Dirección de Investigación de Manizales DIMA, de la Universidad Nacional de Colombia, por el apoyo económico a los semilleros de investigación 15704 y 15599 (Estudio cinético de la degradación térmica de PMMA y PLA).

REFERENCIAS

[1] W. M. Wendlandt, Thermal Analysis, 3 ed., New York: John Wiley & Sons, 1986.

[2] D. S. Achilias, et al., ''Thermal degradation kinetics and isoconversional analysis of biodegradable poly(3-hydroxybutyrate)/organomodified montmorillonite nanocomposites,'' Thermochimica Acta, vol. 514, pp. 58-66, 2011.

[3] B. Liu, et al., ''Thermal degradation kinetics of poly(N-adamantyl-exo-nadimide) synthesized by addition polymerization,'' Journal of Applied Polymer Science, vol. 103, pp. 3003-3009, 2007.

[4] C. L. Wagoner and E. Winergartner, ''Further development of the burning profile,'' Journal of Engineering for Power, vol. 95, no. 2, p. 119–123, 1973.

[5] O. Fadzilah and S. Halim, ''Coal combustion studies using thermogravimetric analysis,'' Journal Mekanikal, vol. 15, pp. 97-107, 2003.

[6] J. Dahiya, et al. ''Kinetics of isothermal and non-isothermal degradation of cellulose: model-based and model-free methods,'' Polymer International, vol. 57, pp. 722-729, 2008.

[7] M. Torrente and M. A. Galán, ''Kinetics of the thermal decomposition of oil shale from Puertollano (Spain),'' Fuel, vol. 80, pp. 327-334, 2001.

[8] J. Cooney, et al., ''Thermal degradation of Poly(ethylene Terephthalate): A kinetic analysis of thermogravimetric data,'' Journal of Applied Polymer Science, vol. 28, pp. 2887-2902, 1983.

[9] S. Jain and M. Sharma, ''Application of thermogravimetric analysis for thermal stability of Jatropha curcas biodiesel,'' Fuel, vol. 93, pp. 252-257, 2012.

[10] J. W. Park et al. ''A kinetic analysis of thermal decomposition of polymer using a dynamic model,'' Polymer Degradation and Stability, vol. 67, pp. 535-540, 2000.

[11] J. Park et al. ''Kinetic analysis of thermal decomposition of polymer using a dynamic model,'' Korean Journal of Chemical Engineering, vol. 17, pp. 489-496, 2000.

[12] H. Yu et al., ''Nonisothermal decomposition kinetics of Nylon 1010/POSS composites,'' Journal of Applied Polymer Science, vol. 113, pp. 17-23, 2009.

[13] A. Aboulkas et al., ''Thermal degradation behaviors of polyethylene and polupropylene. Part I: Pyrolysis,'' Energy Conversion and Management, vol. 51, pp. 1363-1369,2010.

[14] J. E. Barrera et al., ''Estudio de la degradación térmica de poli(alcohol vinílico),'' Revista Ingeniería e Investigación, vol. 27, no. 2, pp. 100-105, 2007.

[15] R. Narayan et al., ''Degradation profiles of polyester-urethane (HP-MDI) and polyester-melamine (HP-HMMM) coatings: a thermal study,'' Journal of Applied Polymer Science, vol. 97, pp. 518-526, 2005.

[16] C. Gamlin et al., ''Influence of ethylene-propylene ratio on the thermal degradation behavior of EPDM elastomers,'' Thermochimica Acta, vol. 367-368, pp. 185-193, 2001.

[17] J. Mano et al., ''Thermal properties of thermoplastic starch/synthetic polymer blends with potential biomedical applicability,'' Journal of Materials Science: Materials in Medicine, vol. 14, pp. 127-135, 2003.

[18] N. Grauper et al., ''Natural and man-made cellulose fibre-reinforced poly(lactic-acid)(PLA) composites: An overview about mechanical characteristics an application areas,'' Composites: Part A, vol. 40, pp. 810-821, 2009.

[19] A. Guo et al., ''Simulated delayed coking characteristics of petroleum residues and fractions by thermogravimetry,'' Fuel Processing Technology, vol. 89, pp. 643-650, 2008.

[20] W. Kim et al., ''Kinetic characterization of thermal degradation process for commercial rubbers,'' Journal of Industrial and Engineering Chemistry, vol. 6, no. 5, pp. 348-355, 2000.

[21] M. Safi et al., ''Global degradation kinetics of pine needles in air,'' Thermochimica Acta, vol. 412, pp. 155-162, 2004.

[22] D. Viquez-Murillo et al., ''Estudio cinético de la degradación isotérmica de la quitina y el quitosano obtenidos a partir del camarón Heterocarpus Vicarius por medio de análisis termogravimétrico,'' Revista Iberoamericana de Polímeros, vol. 11, no. 2, pp. 118-133, 2010.

[23] L. Nuñez and M. Villanueva, ''Influence of the curing cycle selection on the thermal degradation of an epoxy-diamine system,'' Journal of Thermal Analysis and Calorimetry, vol. 80, no. 1, pp. 141-146, 2005.

[24] S. Betancourt et al., ''Degradación térmica de fibras naturales procedentes de la calceta de plátano (estudio cinético),'' Suplemento de la Revista Latinoamericana de Metalurgia y Materiales, vol. 1, no. S1, pp. 215-219, 2009.

[25] J. Criado et al., ''Un nuevo método de análisis térmico: el análisis térmico a velocidad de transformación controlada (ATVC),'' Boletín de la Sociedad Española de Cerámica y Vidrio, vol. 26, pp. 3-11, 1987.

[26] S. Montero, ''Estudio de la cinética implicada en la descomposición termogravimétrica del residuo de aceituna. Emisiones asociadas.'', Tesis de maestría, Dpto. Fís. Apl., Univ. Zaragosa, Zaragosa, España, 2011.

[27] J. Criado et al., ''A critical study of the suitability of the Freeman and Carroll method for the kinetic analysis of reactions of thermal decomposition of solids,'' Thermochimica Acta, vol. 54, p. 1982, 1982.

[28] Y. Márquez et al., ''Estudio de la degradación térmica de mezclas de polilactonas y poli(carbonato de trimetileno) con interés en aplicaciones biomédicas'', Tesis de maestría, Dept. Eng. Quím., Univ. Politècnica de Catalunya, Barcelona, España, 2012.

[29] C. Deng et al., ''Kinetic analysis of solid-state reactions: evaluation of approximations to temperature integral and their applications,'' Solid State Science, vol. 11, pp. 1375-1379, 2009.

[30] V. M. Gorbachev, ''A solution of the exponential integral in the non-isothermal kinetics for linear heating,'' Journal of Thermal Analysis and Calorimetry, vol. 8, pp. 349-350, 1975.

[31] H. Chen et al., ''Error of kinetic parameters for one type of integral method for thermogravimetric measurements,,'' Polymer Degradation and Stability, vol. 90, pp. 132-135, 2005.

[32] J. H. Flynn, ''The 'Temperature Integral' – Its use and abuse,'' Thermochimica Acta, vol. 300, pp. 83-92, 1997.

[33] J. Orfão, ''Review and evaluation of the approximations to the temperature integral,'' AIChE Journal, vol. 53, pp. 2905-2915, 2007.

[34] J. Zsakó, ''Empirical formula for the exponential integral in non-isothermal kinetics,'' Journal of Thermal Analysis and Calorimetry, vol. 8, pp. 593-596, 1975.

[35] N. Liu et al., ''Error evaluation of integral methods by consideration on the approximation of temperature integral,'' Journal of Thermal Analysis and Calorimetry, vol. 81, pp. 99-105, 2005.

[36] H. Chen and N. Liu, ''Approximations for the temperature integral,'' Journal of Thermal Analysis and Calorimetry, vol. 92, pp. 573-578, 2008.

[37] G. I. Senum and R. T. Yang, ''Rational approximations of the integral of the Arrhenius function,'' Journal of Thermal Analysis and Calorimetry, vol. 11, pp. 445-447, 1977.

[38] C. L. Chiang et al., ''Flame retardance and thermal degradation of new epoxy containing silicon and phosphorous hybrid ceramers prepared by the sol-gel method,'' Polymer Degradation and Stability, vol. 77, pp. 273-278, 2002.

[39] W. B. Wan et al., ''Thermal stability evaluation of palm oil as energy transport media,'' Energy Conversion & Management, vol. 46, pp. 2198-2215, 2005.

[40] S. Mallakpour and M. Taghavi, ''The accuracy of approximation equations in the study of thermal decomposition behavior of some systhesized optically active polyamides,'' Iranian Polymer Journal, vol. 18, no. 11, pp. 857-872, 2009.

[41] W. Tang et al., ''New approximate formula for Arrhenius temperature integral,'' Thermochimica Acta, vol. 408, pp. 39-43, 2003.

[42] C. Junmeng et al., ''A new formula approximating the Arrhenius integral to perform the non-isothermal kinetics,'' Chemical Engineering Journal, vol. 124, pp. 15-18, 2006.

[43] R. J. Flores, ''Study of the behavior of non-arrhenius first order kinetic expressions'', M.S. thesis, Dept. Chem. Eng., Texas Tech Univ., Lubbock, TX, USA, 1988.

[44] L. Liau and D. S. Viswanath, ''Thermal Degradation of Poly(vinylbutyral)/Ceramic Composites: A Kinetic Approach,'' Industrial Engineering Chemical Research, vol. 37, no. 1, pp. 49-57, 1998.

[45] K. Baloch et al., ''Application of different methods for the thermogravimetric analysis of,'' Journal of Applied Polymer Science, vol. 120, pp. 3511-351, 2011.

[46] H. T. Kim and S. Oh, ''Kinetics of thermal degradation of waste polypropylene and high-density polyethylene,'' Journal of Industrial and Engineering Chemistry, vol. 11, no. 5, pp. 648-656, 2005.

[47] L. Reich and S. S. Stivala, ''Computer-determined kinetic parameters from TG curves,'' Thermochimica Acta, vol. 36, no. 1, pp. 103-105, 1980.

[48] X. Li et al., ''Non-isothemal termal decomposition reaction kinetics of dimethylhexane-1,6-dicarbamate (HDC),'' Journal of Hazardous Materials, vol. 198, pp. 376-380, 2011.

[49] J. C. Santos et al., ''Thermal stability and kinetic study on thermal decomposition of commercial edible oils by thermogravimetry,'' Journal of Food Science, vol. 67, no. 4, pp. 1393-1398, 2006.

[50] X. L. Wang et al., ''Thermogravimetric analysis of the decomposition of poly(1,4-dioxan-2-one)/starch blends,'' Polymer Degradation and Stability, vol. 81, pp. 415-421, 2003.