ARTÍCULOS

Análisis comparativo de modelos hidrológicos de simulación continua en cuencas de alta montaña: caso del Río Chinchiná

Comparative analysis of continuous simulation hydrological models in high-mountain watersheds: Chinchiná River case

Olga Lucía Ocampo^*; Jorge Julián Vélez^**

* Maestría en Ingeniería Química. Estudiante Doctorado Ingeniería-Línea Automática. Universidad Nacional de Colombia sede Manizales. olocampol@unal.edu.co. Docente Investigador de la Universidad Autónoma de Manizales. Antigua Estación del Ferrocarril. Manizales. Tel: 8727272. olocampo@autonoma.edu.co.

** Ph. D. en Planificación y Gestión de Recursos Hídricos por la Universidad Politécnica de Valencia, España. Profesor Asociado de la Universidad Nacional de Colombia sede Manizales. Facultad de Ingeniería y Arquitectura, Instituto Estudios Ambientales IDEA. jjvelezu@unal.edu.co.

Recibido: 02/04/2013
Aceptado: 06/09/2013

RESUMEN

La modelación hidrológica es la base para la gestión integral del recurso hídrico; en cuencas de alta montaña, e involucra una compleja interacción de procesos fisicoquímicos. Este estudio, realizado en la cuenca del río Chinchiná, Colombia, plantea un análisis multimodelo para capturar la incertidumbre asociada con la modelación hidrológica, mediante la aplicación de siete modelos hidrológicos, lluvia-escorrentía de simulación continua, agregados a escala mensual, con diferentes niveles de complejidad. La capacidad de reflejar la respuesta hidrológica fue analizada por métodos gráficos y estadísticos. Los resultados expresados en los indicadores estadísticos, los hidrogramas y las curvas de duración de caudales permiten una mejor compresión de la escorrentía en cuencas de alta montaña. Los modelos conceptuales Tetis, abcd y el modelo auto-regresivo ARMA (1,1) Salas & Smith capturaron de manera satisfactoria la descarga media y podrían ser aplicados para la estimación en cuencas no aforadas en la zona de estudio.

PALABRAS CLAVE

análisis multimodelo, cuencas no aforadas, modelos hidrológicos, simulación continua.

ABSTRACT

Hydrological modelling is the basis for the comprehensive management of hydrological resources, and in the case of high-mountain watersheds, it involves a complex physicochemical process interaction. This study, conducted in the Chinchiná river watershed (Colombia), poses a multi-model analysis in order to capture the uncertainty associated with the hydrological modelling by means of seven hydrological models, continuous simulation rain-runoff, monthly-scale aggregates, with different complexity levels. The capability to reflect the hydrological response was analyzed through graphical and statistical methods. The results exhibited in the statistical indicators, the hydrographs, and the discharge duration curves allow a better compression of the runoff in high-mountain watersheds. The Tetis and abcd concept models, as well as the ARMA (1,1) Salas & Smith auto-regressive model, satisfactorily captured the mean discharge, and they could be applied for the estimation in non-appraised watersheds in the zone of the study.

KEY WORDS

multi-model analysis, non-appraised watersheds, hydrological models, continuous simulation.

Introducción

A escala de cuenca, la producción de escorrentía involucra una compleja interacción de procesos físicos y químicos que operan a diferentes escalas espaciales y temporales. Estas interacciones han sido estudiadas en las regiones tropicales y permiten comprender la importancia de la estimación de la escorrentía a partir de modelos hidrológicos de simulación continua [1-2].

El balance de agua es afectado por las condiciones climáticas y los cambios en el uso del suelo, que influyen en la infiltración y la percolación, procesos que determinan los caudales máximos, la retención de humedad del suelo y la regulación hídrica [3-4]. En cuencas tropicales, debido a las propiedades del suelo y a las tasas altas de precipitación, el flujo rápido domina los hidrogramas [5]. En cuencas con una gran extensión de pastos, el flujo base domina la generación del flujo a pesar de las marcadas pendientes y altas tasas de precipitación [5-6].

La predicción de flujos de agua en una cuenca requiere el uso de modelos, los cuales deben ser evaluados para diferentes condiciones ambientales (climáticas, topográficas, suelos y cobertura vegetal). Los modelos hidrológicos buscan capturar los mecanismos físicos de generación de la escorrentía superficial y la recarga a los acuíferos subterráneos a partir de la precipitación y la evapotranspiración [7].

Estos modelos hidrológicos son frecuentemente clasificados en tres tipos [8-9]: 1) empíricos o de caja negra donde la solución se basa en parámetros empíricos, calculados por la identificación de relaciones estadísticamente significativas entre ciertas variables. 2) teóricos que están descritos por ecuaciones diferenciales y siguen las leyes de la física y/o procesos químicos; 3) conceptuales que son representaciones simplificadas de los procesos físicos, en términos matemáticos y simulan procesos complejos basándose en parámetros clave conceptuales.

La selección objetiva del modelo es un paso crucial en la modelación para predecir con exactitud caudales y otras variables y entender las respuestas de las cuencas hidrográficas [10]. Para un análisis de caso en particular, el propósito del estudio, el modelo y la disponibilidad de datos son los factores que determinan la selección [7]. Por ejemplo, los modelos de balance, precipitación-escorrentía se han aplicado para evaluar la gestión de recursos hídricos a escala regional, mientras que los conceptuales de parámetro globalizado se han utilizado en la evaluación detallada del flujo superficial [7]. Por otra parte, los modelos distribuidos son necesarios para la simulación de los patrones espaciales de respuesta hidrológica dentro de una cuenca [11-12].

A escala mensual, los modelos conceptuales de balance hídrico se han empleado para diferentes aplicaciones como [7]: síntesis de los registros de largo plazo; generación de los registros de escorrentía para cuencas no aforadas; suministro de datos hidrológicos como insumos para la validación de modelos determinísticos; predicción de la producción dentro de uno o dos meses para el control en tiempo real de sistemas de recursos hídricos; derivación de clasificaciones regionales climáticas e hidrológicas y previsión de posibles efectos hidrológicos del cambio de uso de la tierra y el cambio climático.

Los modelos estadísticos en especial los auto-regresivos de medias móviles se han aplicado a procesos hidrológicos estacionales univariados, con el objetivo de pronosticar, completar datos y generar series sintéticas que conserven los principales estadísticos y la función de autocorrelación de la serie original [13].

Aunque la selección del modelo es crucial, los estudios de modelación hidrológica deberían comparar varios modelos que representen diversos mecanismos para definir la escorrentía [5]. El análisis multimodelo es un método que permite no solo evaluar la capacidad de los modelos de reflejar el comportamiento de la cuenca sino de estimar la incertidumbre de la modelación [12,14-15].

En este estudio, producto de una investigación cuantitativa de tipo descriptivo, realizada en la cuenca del río Chinchiná (Colombia), se analizaron siete modelos hidrológicos agregados, con diferentes grados de complejidad para la simulación del proceso lluvia-escorrentía, basados en los datos observados reportados por las estaciones localizadas en la cuenca. La calibración y la validación permitieron seleccionar los modelos conceptuales de balance y físicamente basados Tetis y abcd, como los que representaron mejor el proceso lluvia-escorrentía en esta cuenca de alta montaña.

1. MATERIALES Y MÉTODOS

1.1. Caso de estudio

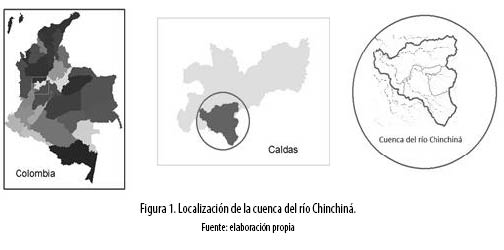
La cuenca del río Chinchiná (1052 km²) está localizada en la región centro sur del departamento de Caldas, Colombia (figura 1). En la parte alta de la cuenca se encuentran ecosistemas estratégicos como los glaciares tropicales del nevado del Ruiz y Santa Isabel, ubicados en el parque nacional natural Los Nevados, los páramos y los bosques de niebla. En la cuenca media prevalece el paisaje cafetero declarado por la UNESCO patrimonio de la Humanidad y en la parte baja predominan los pastos y los cultivos de cítricos.

La información detallada sobre el área de estudio, incluyendo topografía, geología, suelos, vegetación y climatología se proporciona en [16]. La topografía de la cuenca es compleja dada su marcada diferencia altitudinal, 5278 a 767 msnm. Debido a la diversidad del material parental, el rango altitudinal y la presencia de todos los pisos térmicos, los suelos presentan un alto grado de heterogeneidad. Con respecto al uso del suelo, las actividades pecuarias, agrícolas y forestales ocupan la mayor extensión.

En esta cuenca andina, el régimen de lluvias está determinado no solo por los factores físicos como la orografía, sino también por el desplazamiento de la zona de confluencia intertropical (ZCIT), la influencia de los vientos alisios que ingresan por el Atlántico, las masas de aire que vienen del Pacífico, los aportes de humedad procedentes del Amazonas [17] y los vientos del oeste que penetran por la costa Pacífica colombiana los cuales provienen de una corriente de bajo nivel muy superficial en el trópico llamada Chorro del Chocó [18].

Las principales variables climáticas siguen un ciclo estacional, de carácter bimodal. Para el período 1981-2010, la temperatura promedio fluctúa entre -2 °C a 25 °C, y la precipitación entre 1175 mm a 2880 mm; la evapotranspiración potencial (ETP) varía con la altitud, según el modelo obtenido a partir del método de Penman-Monteith por CENICAFE [17]; la ETP anual oscila entre 555 mm a 1370 mm, mientras que la evapotranspiración real anual calculada por el método de Turc fluctúa entre 240 mm a 885 mm.

1.2. Modelos

Para efectuar el balance hidrológico fueron empleados modelos agregados a escala mensual, de tipo conceptual que preservan el balance, y modelos auto-regresivos. La modelación agregada considera la cuenca como una entidad espacialmente singular en la cual el valor medio de los parámetros es representativo para toda la cuenca. Emplea una función de transferencia matemática para el modelamiento de los procesos hidrológicos significativos y sus interrelaciones [7].

Los modelos conceptuales de balance hídrico a escala mensual pretenden simular los procesos hidrológicos por la conceptualización de la cuenca como un conjunto de tanques interconectados, a través de los cuales el agua pasa de la entrada como lluvia a la salida como caudal; las ecuaciones de control satisfacen los requerimientos de balance de agua. Los primeros modelos de balance de escala mensual fueron desarrollados por Thornthwaite (1948) y desde entonces se han aplicado y adaptado a un amplio espectro de problemas hidrológicos [7, 22]. Estos modelos van desde los conceptuales relativamente complejos, con 10 a 15 parámetros a muy simples de 2 a 5 parámetros.

Para el estudio se emplearon los modelos conceptuales y físicamente basados: Tetis, Témez, abcd; se incluyeron los modelos clásicos recomendados por Alley [19]: T y P.

Finalmente, fueron evaluados los modelos autorregresivos de medias móviles –ARMA– (Autoregressive Moving Average) [13], los cuales se utilizan para la descripción y pronóstico de las series temporales. Son modelos matemático-estadísticos escritos con ecuaciones de diferencias para una serie de tiempo, que sintetizan en una sola expresión las componentes auto-regresiva y de media móvil.

1.2.1. Modelo Tetis

Tetis es un modelo conceptual, de balance y físicamente basado; consiste en cinco tanques, los cuales corresponden [20]: 1) Almacenamiento estático: las salidas son las producidas por la evapotranspiración. 2) Almacenamiento superficial: el agua que no es infiltrada está disponible para ser escurrida superficialmente. 3) Almacenamiento gravitacional: dentro del cual se percola la cantidad que el subsuelo, en estado de saturación, es capaz de trasportar en sentido vertical; el resto queda disponible para conformar el flujo subsuperficial. 4) Corresponde al acuífero: el agua que ingresa en profundidad representa las pérdidas del sistema y el flujo horizontal es el flujo base.

1.2.2. Modelo Témez

El modelo Témez [21] es un modelo de tanques que se divide en dos zonas; en la primera, la lluvia se almacena en forma de humedad y en ella, dependiendo de la humedad, de la capacidad máxima de almacenamiento y de la evapotranspiración potencial se origina un excedente que consta de dos componentes, la escorrentía superficial y la infiltración que se almacena en el acuífero.

1.2.3. Modelo Abcd

El modelo hídrico agregado de balance, abcd [22], ha sido aplicado para la gestión de los recursos hídricos y el estudio de la evolución de los regímenes hidrológicos en el largo plazo. Está divido en tres tanques: el primero corresponde al almacenamiento superficial, el segundo a la zona no saturada, el último es la zona saturada donde se presenta el almacenamiento subterráneo.

1.2.4. Modelo T

El Modelo T es simple de un único tanque [19], que representa el suelo. La capacidad de almacenamiento de humedad del suelo depende de la precipitación, de la humedad y la evapotranspiración potencial (ETP). El exceso se convierte en escorrentía y parte del agua almacenada se infiltra a capas más profundas del suelo [23].

1.2.5. Modelo P

El Modelo P [24] es similar al modelo T, pero divide el suelo en dos tanques; la capa o tanque superior se humedece primero que la capa inferior, la cual no puede modificarse hasta que la humedad superior se sature. La evapotranspiración se produce en primera instancia en la capa superior y luego es posible la evapotranspiración desde la capa inferior. En el momento que se presente en el límite inferior de las dos capas una capacidad máxima de almacenamiento de humedad se origina la escorrentía [23].

1.2.6. Modelos autorregresivos

Los modelos autorregresivos de medias móviles ARMA sintetizan en una sola expresión las componentes autorregresiva y de promedio móvil de una serie de tiempo. Con la primera componente autorregresiva, se determina cada observación como una combinación lineal de las observaciones anteriores, y con la segunda componente, de promedio móvil, se incluye una parte aleatoria que completa la descripción del fenómeno a través del tiempo. Por tanto, se considera que la serie temporal tiene señal –parte determinística del fenómeno dinámico– y ruido –perturbaciones aleatorias que sufre por causas exógenas– [13-25].

1.3. Información climática

Para la modelación se tomó como base la información de las estaciones localizadas en el cauce principal del río Chinchiná (tabla 1). Los registros de temperatura y precipitación de las estaciones fueron empleados para el balance hidrológico. La radiación solar fue calculada con las correlaciones propuestas por [26], tomando como base los registros de humedad relativa y brillo solar de las estaciones climatológicas. La ETP fue calculada con el método de Thornthwaite, con el cual se obtuvo en promedio, valores 3.4 % menores que los estimados con la ecuación propuesta por CENICAFÉ [17].

1.4. Calibración y validación

La principal desventaja de los modelos conceptuales estriba en el concepto de equifinalidad [27], es decir, la existencia de diferentes valores de los parámetros del modelo con los que se obtienen similares medidas de ajuste. Sin embargo, las actuales técnicas de calibración y validación, y un análisis detallado de la estructura del modelo y de la incertidumbre de los parámetros permiten reducir este problema. Por tanto, para cada uno de los modelos, se realizó el proceso de calibración y validación con la técnica Split sample [28], acompañado de un análisis de las curvas de duración.

La calibración es la estimación de los parámetros del modelo, mediante la comparación de las predicciones para un conjunto determinado de condiciones, con los datos observados [29]. Busca mejorar el ajuste entre las observaciones y las simulaciones de la variable de salida de interés, al variar reiterativamente los parámetros del modelo.

Los mejores parámetros de calibración fueron seleccionados basados en el análisis gráfico y los parámetros estadísticos. Las técnicas gráficas proporcionan una comparación visual de los datos simulados y observados y una primera visión general de los resultados del modelo. Para el estudio, se emplearon hidrogramas o gráficos de series de tiempo del flujo simulado, que ayudan a identificar el sesgo del modelo, las diferencias en el tiempo, la magnitud de los caudales máximos y la forma de las curvas de recesión [29].

Los parámetros estadísticos evaluados fueron: el índice de eficiencia de Nash-Sutcliffe-NSE, el sesgo porcentual (Percent bias-PBIAS), la razón RSR que relaciona la raíz cuadrada del error medio (RMSE-Root Mean Square Error) y la desviación estándar de las observaciones, y la interpretación física de dichos parámetros. Para tal efecto, se consideraron los rangos de los parámetros estadísticos de la tabla 2.

Una vez lograda una adecuada calibración, se evaluó nuevamente el ajuste del modelo, para un nuevo set de variables de entrada y salida, sin ajustar los parámetros previamente calibrados, es decir, se validó el modelo [29]. Con los modelos calibrados y validados, se realizó la simulación para los períodos 1981-2009 y 1971-2000.

La validación de la consistencia final de los parámetros y de los resultados obtenidos se efectuó mediante la observación de las curvas de duración de caudales.

2. RESULTADOS Y DISCUSIÓN

2.1. Calibración y validación de modelos

La calibración fue realizada en la estación El Retiro, ubicada a la salida de la cuenca, para el período 2001-2007. De acuerdo con la evaluación de las funciones estadísticas objetivo, que se presentan en la tabla 3 y en la figura 2, los mejores resultados se obtuvieron con los modelos TETIS, abcd y ARMA (1,1) Salas y Smith; sin embargo, todos los modelos fueron calibrados satisfactoriamente.

La validación se efectuó para el período 1987-1993, con los mismos parámetros obtenidos durante el proceso de calibración. Los resultados comparativos se presentan en la tabla 3 y en la figura 2. La validación fue satisfactoria para los modelos Tetis, abcd, Témez y los modelos auto-regresivos. Con los modelos T y P los resultados de la validación no fueron satisfactorios y no fue posible encontrar mejores parámetros para incrementar los valores del índice de eficiencia de Nash-Sutcliffe-NSE y reducir el error RSR, lo cual era de esperar, dada la simplicidad de estos modelos y la complejidad de la cuenca de alta montaña objeto de estudio.

2.2. Simulación

La simulación fue realizada en la estación El Retiro, y se emplearon todos los modelos para efectos de comparación. Para el período de simulación 1981-2009, los resultados de los parámetros estadísticos se consolidan en la tabla 3 y en la figura 2. Basados en el análisis gráfico y estadístico fueron satisfactorios los resultados obtenidos con los modelos Tetis, abcd y ARMA (1,1) Salas & Smith; los errores de balance en la modelación hidrológica se estimaron en 5.7 %, -2 % y -5.4 %, respectivamente.

La simulación para la normal climatológica calcula para el período 1971-2000 también fue realizada; se obtuvieron resultados satisfactorios con los modelos Tetis, abcd y ARMA (1,1) Salas y Smith, con errores de balance de 1.8%, 7.8% y 11.5%, respectivamente.

La simulación con los modelos T y P, Témez y Arma (1,1) no se consideró satisfactoria porque el estadístico RSR superó los valores de 0.7, para los dos períodos evaluados.

Los curvas de duración de caudales para el período 1981-2009 se muestran en la figura 3 y permiten corroborar que los modelos Tetis, abcd y ARMA (1,1) Salas & Smith simulan de manera satisfactoria tanto los valores medios como los mínimos; sin embargo, presentan diferencias con los valores máximos para probabilidades mayores al 90 %. Este hecho también se confirma con los hidrogramas (figura 4) y las curvas de correlación de caudales simulados frente a los observados (figura 5), donde es evidente la subestimación de los caudales máximos. Es de anotar que el modelo Témez presentó un menor error en la modelación de los caudales máximos; sin embargo, tuvo limitaciones para la modelación de los mínimos y la dispersión es mayor, lo cual explica el resultado no satisfactorio del período de simulación. Con los otros modelos que obtuvieron evaluaciones no satisfactorias, T, P y Arma (1,1), se tienen diferencias con las descargas tanto con las máximas como con las mínimas.

3. CONCLUSIONES

Este trabajo tuvo como objetivo analizar el comportamiento de siete modelos lluvia-escorrentía con respecto a la descarga medida. Los resultados han demostrado que los indicadores estadísticos y una inspección de los hidrogramas y las curvas de duración de caudales pueden facilitar una mejor comprensión de la escorrentía en ríos de alta montaña. El ejercicio de validación realizado con la curva de duración de caudales es necesario para dar sentido físico e hidrológico a los resultados del proceso de calibración y validación. Para el caso del río Chinchiná, la aplicación de la técnica multimodelo permite observar la incertidumbre asociada a la modelación hidrológica. Los modelos Tetis, abcd y ARMA (1,1) Salas & Smith simularon bien la descarga promedio y mínima según los criterios de eficiencia; los indicadores estadísticos fueron catalogados como buenos para Tetis y satisfactorios para abcd y ARMA (1,1) Salas & Smith para el período 1981-2009, por lo que pueden ser utilizados en las microcuencas no aforadas y para la planificación y gestión de los recursos hídricos; sin embargo, estos modelos no reflejan adecuadamente los caudales máximos.

AGRADECIMIENTOS

Los autores quieren agradecer a la Corporación Autónoma Regional de Caldas –CORPOCALDAS–, el Centro Nacional de Investigaciones del Café –CENICAFÉ–, el Instituto de Estudios Ambientales –IDEA– y a la Central Hidroeléctrica de Caldas –CHEC S. A. – quienes han colaborado para el desarrollo de esta investigación. Al proyecto VACEA ''Vulnerability and Adaptation to Climate Extremes'' y al Programa de ''Fortalecimiento de capacidades conjuntas para el procesamiento y análisis de información ambiental'' de la Universidad Nacional de Colombia Sede Manizales.

REFERENCIAS

[1] R. Celleri and J. Feyen, ''The hydrology of tropical Andean ecosystems: importance, knowledge status and perspectives'', Mount. Res. Development, vol. 29, pp. 350-355, 2009.

[2] R. O. Figueiredo, D. Markewitz, E. A. Davidson, A. E. Schuler, O. S. Watrin and P. de Souza Silva, ''Land-use effects on the chemical attributes of low order stream in the eastern Amazon'', J. Geophys, vol. Res 115, 2010.

[3] L. A. Bruijnzeel, ''Hydrological functions of tropical forests: not seeing the soil for the trees?'', Agric. Ecosyst. Environ. vol. 104, pp. 185-228, 2004.

[4] H. Elsenbeer, ''Hydrologic flow paths in tropical forest soilscapes-a review'', Hydrol. Proc., n.° 15, pp. 1751-1759, 2001.

[5] Plesca, E. Timbea, J. F. Exbrayat, D. Windhorst, P. Krafta, P. Crespo, K. B. Vache, H. G. Frede and L. Breuer, ''Model intercomparison to explore catchment functioning: results from a remote montane tropical rainforest'', Ecological Modeling, n.° 239, pp. 3-13, 2012.

[6] A. Bucker, P. Crespo, H. G. Frede, K. Vache, F. Cisneros and L. Breuer, ''Identifying controls on water chemistry of tropical cloud forest catchments: combining descriptive approaches and multivariate analysis'', Aqua. Geochem, n.° 16, pp. 127-149, 2010.

[7] C. Y. Xu and V. P. Singh, ''Review on regional water resources assessment models under stationary and changing climate'', Water Resources Management, vol. 18, n.° 6, pp. 591-612, 2004.

[8] V. P. Singh, Watershed Modeling. In computer Models of Watershed Hydrology, Colorado: Water Resources Publication, 1995.

[9] V. M. Ponce, Engineering Hydrology: Principles and practices, Englewood Cilffs: Prentice Hall, 1989.

[10] M. P. Clark, A. G. Slater, D. E. Rupp, R. A. Woods, J. A. Vrugt, H. V. Gupta, T. Wagener and L. E. Hay, ''Framework for Understanding Structural Errors (FUSE): A modular framework to diagnose differences between hydrological models'', Water Resources Research, vol. 44, pp. 1-14, 2008.

[11] K. Beven, ''Changes ideas in hydrology- The case of physically based models'', J Hydrol, n.° 105, pp. 157-172, 1989.

[12] S. Reed, V. Koren, M. Smith, Z. Zhang, F. Moreda and D. J. Seo, ''Overall distributed model intercomparison project results'', J. Hydrol, no. 298, pp. 27-60, 2004.

[13] J. D. Salas and J. B. Obeysekera, ''Conceptual basis of seasonal streamflow time series model'', J. Hydraul. Eng., vol. 8, n.° 118, pp. 1186-1194, 1992.

[14] J. C. Refsgaard, J. P. Van der Sluijs, A. L. Hojberg and P. A. Vanrollenghem, ''Uncenrtainty in the environmental modeling process- a framework and guidance'', Environ. Model. Software, n.° 22, pp. 1543-1556, 2007.

[15] L. Breuer, J. A. Huisman, P. Willems, H. Bormann, A. Bronstert, B. F. Croke, H. G. Frede, T. Graff, L. Hubrechts, A. J. Jakeman, G. Kite, J. Lanini, G. Leavesley, D. P. Lettenmaier, G. Lindstrom, J. Seibert, M. Sivapalan and N. R. Viney, ''Assessing the impact of land use change on hydrology by ensemble modeling (LUCHEM) I: Model Intercomparison with current land use'', Adv. Water Resour, n.° 32, pp. 129-146, 2009.

[16] O. L. Ocampo, J. J. Vélez and A. Londoño, Análisis de vulnerabilidad hídrica de la cuenca del río Chinchiná, Manizales: Universidad Nacional de Colombia, 2013.

[17] A. Jaramillo, Clima andino y café en Colombia, Chinchiná: CENICAFE, 2005.

[18] G. Poveda, P. R. Waylen and R. S. Pulwarty, ''Annual and inter-annual variability of the present climate in northern South America and South Mesoamerica'', Paleogeography, Palaeoclimatology, Palaeoecology, n.° 234, pp. 3-27, 2006.

[19] W. M. Alley, ''On the treatment on evapotranspiration, soil moisture accounting, and aquifer recharge in monthly water balance models'', Water Resources Research, vol. 8, n.° 20, pp. 1137-1149, 1984.

[20] F. Francés, J. I. Vélez and J. J. Vélez, ''Split parameter structure for the automatic calibration of distributed hydrological models'', Journal of Hydrology, n.° 332, pp. 226-240, 2007.

[21] J. R. Témez, ''Cálculo Hidrometeorológico de caudales de avenidas en pequeñas cuencas naturales'', Ingeniería Civil y Medio Ambiente, 1978.

[22] H. A. Thomas, ''Improved methods for rational water assessment report,'' US Water Resources Council, Washington DC., 1981.

[23] Correa, ''Implementación del Modelo T para el balance hídrico empleando la herramienta computacional HidroSIG-Java'' Pontificia Universidad Javeriana, Bogotá, 2005.

[24] Palmer, ''Meteorological drought,'' Washington DC, 1965.

[25] Box and Jenkins, Time series Analysis: Forecasting and Control, San Francisco: Holden Day, 1976.

[26] R. K. Swartman and O. Ogulande, ''An investigation on packed bed collectors'', Solar energy, vol. 3, n.° 10, pp. 106-110, 1966.

[27] K. J. Beven, ''Prophecy, reality and uncertainty in distributed hydrological modeling'', Advances in water resources, vol. 1, n.° 16, pp. 41-51, 1993.

[28] V. P. Singh, Hydrologic Systems-Rainfall-Runoff Modeling, Englewood Cliffs, NJ: Prentice Hall, 1988.

[29] D. N. Moriasi, J. G. Arnold, M. W. Van Liew, R. L. Bingner, R. D. Harmel and T. L. Veith, ''Model Evaluation Guidelines for systematic quantification of accuracy in watershed simulations'' A. Society of Agricultural and Biological Eng, vol. 50, n.° 3, p. 885-900, 2007.