ARTÍCULOS

Predicción de los precios de contratos de electricidad usando programación genética con bloques funcionales

Electricity contract price prediction using genetic programming with functional blocks

Carlos A. Martínez^*; Juan D. Velásquez^**

* Estudiante, Doctorado en Ingeniería – Ingeniería de Sistemas e Informática, Universidad Nacional de Colombia, Medellín, Colombia (2013) ; Magíster en Ingeniería de Sistemas, Universidad Nacional de Colombia, Medellín, Colombia (2012). Dirección de correspondencia: Universidad Nacional de Colombia. Facultad de Minas. Cra 80 65-223, Bloque M8A, Of. 206. Medellín, Colombia. Tel +57 +4 425 5350. Correo electrónico: amartin@unal.edu.co

** Doctor en Ingeniería, Área de Sistemas Energéticos, Universidad Nacional de Colombia, Medellín, Colombia (2009); Magíster en Ingeniería de Sistemas, Universidad Nacional de Colombia, Medellín, Colombia (1997); Profesor Asociado de la Universidad Nacional de Colombia (sede Medellín, Colombia). Dirección de correspondencia: Universidad Nacional de Colombia. Facultad de Minas. Cra 80 65-223, Bloque M8A, Of. 206. Medellín, Colombia. Tel. +57 +4 425 5370. Correo electrónico: jdvelasq@unal.edu.co

Recibido: 22/05/2013
Aceptado: 06/09/2013

RESUMEN

La predicción de los precios de los contratos en los mercados energéticos desregularizados es la clave para la toma de decisiones estratégicas de negocio y operativas por los agentes del mercado. En este trabajo se predicen los precios promedio de los contratos vendidos en el mercado eléctrico colombiano, utilizando un algoritmo de programación genética modificado. El modelo desarrollado es capaz de capturar la dinámica intrínseca de los precios y las predicciones de precios para los próximos meses con mayor precisión que los modelos ARIMA y DAN2 para horizontes de predicción de 12 y 24 meses, reportados en la literatura

PALABRAS CLAVE

precios de la electricidad; programación genética; predicción; series de tiempo; bloques funcionales.

ABSTRACT

The prediction of the prices of the contracts in non-regulated electric energy markets is the key for the market agents to make strategic business and operational decisions. The average prices of the contracts sold in the Colombian electric energy market are predicted in this study by means of a modified genetic programming algorithm. The developed model is capable of capturing the intrinsic dynamics of the prices and the price predictions for the upcoming months with a more accurate precision than the ARIMA and DAN2 models for prediction horizons of 12 and 14 months, as they have been reported in the literature.

KEY WORDS

electricity prices; genetic programming, prediction, time series, functional blocks.

INTRODUCCIÓN

En los últimos años la predicción de series de precios ha sido de gran importancia, principalmente en los mercados de energía, debido a la desregularización de los mercados de precios de compra y venta, y la complejidad inherente a la modelación de series temporales.

En los precios de la electricidad influyen varios factores: las características físicas del sistema de generación, las decisiones de negocio de los distintos agentes y la regularización [1]. Lo anterior conlleva que en las series de precios de la energía se presenten: componentes cíclicos estacionales con periodicidad de corto y largo plazo, volatilidad variable en el tiempo, cambios estacionales, valores extremos, correlaciones de alto orden y tendencias locales [2], que generan alta complejidad en la generación de modelos la modelación y predicción de las series temporales.

Adicionalmente, se presenta que los agentes del mercado utilizan contratos para la negociación de la electricidad, como mecanismo de mitigación del riesgo asociado a las fluctuaciones de corto plazo, protegiendo así al comprador de precios excesivamente altos, como al vendedor de precios demasiado bajos.

Desde la liberalización del mercado eléctrico colombiano, se estableció que la electricidad puede ser negociada en la Bolsa de Electricidad o a través de contratos bilaterales entre agentes. Actualmente, existen dos tipos principales de contratos: pague-contratado y pague-demandado. Pague-contratado consiste en que el comprador debe pagar la totalidad de la electricidad contratada; mientras que, en pague-demandado, el comprador solo se compromete a pagar la energía efectivamente consumida.

Es así que la predicción de los precios de la electricidad es una necesidad constante de los distintos agentes de mercado para planear y desarrollar sus estrategias de negociación y generación de energía.

En la literatura se han reportado experiencias sobre el pronóstico de series de precios de la energía utilizando perceptrones multicapa (MLP, por su sigla en inglés), redes neuronales artificiales, modelos DAN2 [3], heurísticas y modelos ARIMA [4]. Sin embargo, los modelos propuestos asumen la estructura funcional de los datos y se concentran en la optimización de parámetros respectivos, sin considerar que pueden corresponder a una mezcla de modelos.

Por otra parte, en la literatura también se presentan algoritmos bio-inspirados que permiten evitar asumir la forma de la función de predicción a priori; por el contrario, la determinan a partir de un espacio de búsqueda definido. Una de las principales técnicas corresponde a la programación genética (GP, por su sigla en inglés). GP puede entenderse como una extensión de los algoritmos genéticos que permite obtener expresiones matemáticas empíricas que aproximan la relación existente y desconocida entre un conjunto de variables independientes y una variable dependiente; es así como en GP, los individuos representan expresiones matemáticas [5]. Para ello, dichas expresiones matemáticas (o individuos en la jerga de los algoritmos genéticos) son representadas como árboles sintácticos donde las funciones y operadores matemáticos (suma, resta, multiplicación, etc.) van en los nodos interiores (o nodos funcionales), y las variables y las constantes numéricas van en los nodos terminales. De esta forma, al aplicar los operadores genéticos de clonación, cruce y mutación sobre una población de individuos, se realiza una búsqueda en el espacio de expresiones matemáticas con el fin de encontrar una ecuación empírica que permita representar la relación existente entre un conjunto de variables de entrada y una variable de salida.

Sin embargo, dado que el algoritmo de GP es principalmente combinatorio, en el cual los terminales corresponden a los rezagos y constantes, no es posible garantizar el uso de todos los rezagos de interés, la inclusión de modelos de predicción de series de tiempo de la literatura, ni limitar el espacio de búsqueda. Por lo anterior, se propone el uso de bloques funcionales (BF) como únicos terminales a ser considerados en la generación de los individuos.

Por lo anterior, el objetivo de este artículo es presentar los resultados obtenidos al pronosticar la serie de precios promedio mensuales de contratos despachados en la Bolsa de Energía de Colombia, GP y comparándolo con los reportados en la literatura usando DAN2 y un modelo ARIMA, y determinar cuál de dichas aproximaciones permite obtener pronósticos más precisos. En este caso se consideran únicamente modelos univariados, ya que no hay estudios que permitan relacionar los precios de los contratos con variables físicas o económicas del mercado de electricidad, ni con la serie de precios de Bolsa. Una presentación profunda sobre el modelo ARIMA, sus propiedades y su proceso de especificación es realizada por Makridakis et al. (1998).

La originalidad e importación de la investigación propuesta se basa en los aspectos:

1. Aunque en la literatura se han presentado casos de predicción de precios de electricidad en mercados de corto plazo [1], el de contratos no ha sido tan nutrido y aún presenta problemas de predicción a horizontes de tiempo superiores a un año.

2. La motivación de este artículo surge desde la necesidad de los agentes de mercado para contar con pronósticos acertados de los precios de la electricidad, que les permitan tomar decisiones adecuadas de negocio. En este artículo se busca evaluar si es posible utilizar el algoritmo de programación genética para el pronóstico de la serie de precios, de tal manera, que sus resultados son una clara señal para la continuación de esta investigación incorporando nuevos avances en GP. Debe aclararse que esta investigación no se centra en los aspectos rigurosos y formales propios del análisis econométrico, sino en los aspectos empíricos de la predicción como un insumo para la toma de decisiones, donde prima la capacidad para obtener el pronóstico más preciso posible, dejando a un lado los aspectos más formales.

3. Se contribuye a difundir el uso de GP para la predicción de series de precios en mercados de electricidad, aumentando así la cantidad de herramientas disponibles.

El resto de este artículo está organizado como se indica a continuación. En la sección 2, se analiza el algoritmo de programación genética y la información del mercado colombiano de precios de la energía. En la sección 3, se reportan los resultados obtenidos usando el algoritmo de GP y se comparan con los resultados obtenidos usando un modelo DAN2 y ARIMA. En la última sección se presentan las respectivas conclusiones.

1 METODOLOGÍA

1.1 Información utilizada

En este trabajo fue analizado el logaritmo natural de la serie de precios mensuales promedio de los contratos despachados en la Bolsa del mercado mayorista de electricidad en Colombia (PCONTRATOS) expresada en $/kWh, entre mayo de 1996, y junio de 2008.

PCONTRATOS es calculada como el promedio de los precios pactados en los contratos en ejercicio durante cada mes, ponderados por la cantidad de energía negociada en cada contrato; cabe precisar que el precio pactado en cada contrato es privado y, por tanto, los agentes del sistema no tienen acceso a este valor. Consecuentemente, la serie en estudio se constituye como la única señal directamente visible para todo el mercado sobre este indicador. Por otra parte, la cantidad de electricidad negociada en contratos corresponde hasta en un 80 % del total de la producción de los agentes generadores en el mercado, los cuales dejan el porcentaje restante para maniobrar en la Bolsa de Energía.

El comportamiento de la serie muestra alta complejidad, debido principalmente a [7]:

• La cantidad de energía liquidada al final del contrato: pague-lo-contratado, pague-lo-demandado, pague-lo-demandado-con-tope.

• El mecanismo para calcular los precios: un único precio fijo para todo el contrato, precio horario fijo, precio amarrado al precio de Bolsa, precio indexado, inclusión de topes máximo y mínimo para el precio del contrato.

• El momento en que fueron firmados los contratos en ejercicio: desde unos pocos meses hasta diez años atrás. No obstante, existe una clara tendencia a que el plazo de los contratos no supere los dos años.

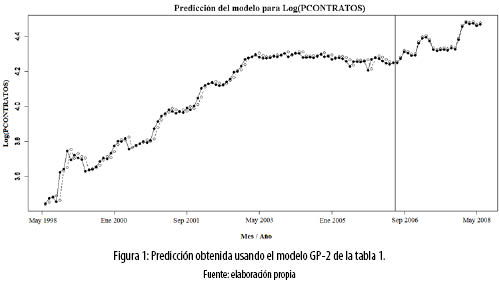
En la figura 1, se puede apreciar la predicción (círculos blancos) de la serie PCONTRATOS desde mayo de 1998 (círculos rellenos), la cual fue analizada por [2], mostrando una tendencia creciente de largo plazo hasta el primer semestre de 2003; durante ese mismo intervalo de tiempo se evidencia una componente cíclica de periodicidad anual de amplitud variable, explicada, posiblemente, por el ciclo invierno-verano. Desde el año 2003 se presenta una tendencia ligeramente descendente que finaliza en algún momento del primer semestre del año 2006. Se evidencia en este momento del tiempo un cambio estructural en la serie, tanto en su tendencia como en su componente cíclica; por una parte, se recuperan los niveles de crecimiento que caracterizaron los años 2000, 2001 y 2002, mientras que, por la otra, se presenta nuevamente un ciclo estacional de período anual, cuyo nivel más alto coincide con la estación de verano [2].

1.2 Metodología empleada

Se incluyeron los artículos que cubren el pronóstico de los indicadores bursátiles mediante lógica difusa, sistemas de inferencia borrosa y sistemas neuro-difusos. Se excluyeron los artículos relacionados con el análisis fundamental o en los que se pronostiquen los precios de acciones particulares.

El algoritmo de programación genética corresponde a una extensión de los algoritmos genéticos (GA, por su sigla en inglés) propuesto por Koza (1992), en los cuales los individuos corresponden a expresiones matemáticas, representadas computacionalmente por árboles sintácticos, por lo general binarios. Los individuos están compuestos por nodos internos llamados nodos funcionales y nodos al final de las ramas llamados nodos terminales. Los nodos funcionales corresponden a los operadores a ser utilizados, suelen corresponder a operaciones aritméticas básicas F = {+, - , *, /}. Los nodos terminales corresponden a las variables de entrada y constantes numéricas (también llamadas parámetros) a ser utilizados .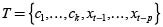

Por otro lado, los operadores genéticos de cruce y clonación son aplicados a los árboles sintácticos, y no solo a valores específicos como en GA.

A continuación se muestra el algoritmo original de GP propuesto por Koza (1992):

1. En la iteración o generación inicial (g = 0) se crea una población (P₀) de n individuos.

2. Para cada individuo S_i, con i = {1,...,n}, se evalúa la función de aptitud f(S_i).

3. Se genera una nueva población 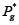aplicando los operadores genéticos a la población actual P_g, de la siguiente forma:

a) Son seleccionados los padres a los cuales se les aplicarán los operadores de cruce y clonación de una manera probabilística.

b) A diferencia de los algoritmos genéticos tradicionales no se considera el operador de mutación por lo que se limita a cruce y clonación.

4. La población de hijos 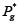se remplaza por la población actual P_g así: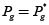

5. Se evalúan los criterios de parada (usualmente es utilizado el número máximo de generaciones); si no se cumplen se vuelve al paso 2. En caso contrario se termina la ejecución del algoritmo.

Por otra parte, en [8] son mostradas las ventajas de utilizar bloques funcionales como únicos terminales a ser considerados en la generación de los individuos. De acuerdo con ello, en este trabajo se toma el algoritmo original de GP con terminales correspondientes a BF.

Los BF corresponden a una función B(.) la cual puede ser evaluada númericamente sin depender de otras funciones externas. B(.) puede entenderse como una combinación lineal de las funciones g_i(.) así: 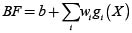, donde X es el vector de entradas (variables/rezagos) del modelo, b y w_i son los parámetros del BF.

2 RESULTADOS Y DISCUSIÓN

La muestra seleccionada corresponde al logaritmo natural de los precios medio mensuales de los contratos despachados en la Bolsa del mercado mayorista de electricidad en Colombia, expresada en $/kWh entre mayo de 1996 y junio de 2008 (PCONTRATOS). La serie consta de 146 observaciones, de las cuales las primeras 122 son utilizadas para entrenamiento del algoritmo y las restantes 24 para validación de pronóstico. Con el fin de analizar distintos horizontes de tiempo de predicción, se separó el conjunto de datos de validación en un año (12 primeras observaciones) y dos años.

Para cada uno de los conjuntos de datos (predicción 1 año y predicción 2 años), fue analizada la bondad de ajuste por medio de la sumatoria del error cuadrático medio (SSE, por su sigla en inglés) y su desviación media absoluta (MAD, por su sigla en inglés).

En la tabla 1, se reportan los resultados obtenidos por la metodología propuesta utilizando GP (GPBF), la metodología tradicional de GP, los cuales fueron resumidos por medio de dos modelos:

• GP-1: Población inicial: 30 individuos; nivel de profundidad máximo inicial 3; Número máximo de generaciones: 10; Función de error: SSE; Número de rezagos: 12. Función de optimización: OPTIM.

• GP-2: Población inicial: 30 individuos; nivel de profundidad máximo inicial 3; Número máximo de generaciones: 10; Función de error: SSE; Número de rezagos: 25. Función de optimización: OPTIM.

• GPBF-1: Población inicial: 100 individuos; nivel de profundidad máximo inicial 30; Número máximo de generaciones: 10; Función de error: SSE; Número de rezagos: 12.

• GPBF-2: Población inicial: 100 individuos; nivel de profundidad máximo inicial 30; Número máximo de generaciones: 10; Función de error: SSE; Número de rezagos: 25.

Adicionalmente, en la tabla 1 se muestran los resultados de los modelos DAN2 y ARIMA reportados en [2].

En la tabla 1 se puede apreciar que el modelo propuesto GPBF-2 presenta el mejor ajuste de pronóstico tanto para un horizonte de 12 meses como para el de 24 meses, con unos SSE (MAD) de 0.006 (0.018) y 0.011 (0.019), respectivamente.

Lo anterior implica que el modelo generado por GPBF-2 presenta tanto un mejor error de aproximación en los pronósticos, como una menor desviación absoluta. Cabe resaltar, además, que GPBF-2 disminuye en un 54 % el SSE de pronóstico a un año con respecto al modelo DAN2-3, el cual es el de menor SSE reportado por [2] y en un 50 % con respecto al modelo ARIMA-3 para el pronóstico a dos años, el cual corresponde al modelo con menor SSE reportado por [2].

Por otra parte, comparando los resultados de GPBF-2 con los resultados del algoritmo tradicional de GP (GP-1 y GP2) también se muestra una mejora del 50 % en el SSE de predicción a un año y del 54 % con respecto al SSE de predicción de dos años con respecto al modelo GP-1. Esto también muestra la mejora registrada en la capacidad de predicción al utilizar bloques funcionales.

Los resultados indican, de forma indirecta, que el modelo GPBF-2 captura adecuadamente la dinámica de la serie PCONTRATOS, respecto a las aproximaciones ARIMA y DAN2.

3. CONCLUSIONES

En este artículo se pronostican los precios promedio de contratos despachados en el mercado eléctrico colombiano, usando el algoritmo de programación genética con bloques funcionales, comparándolos con los reportados por modelos ARIMA y DAN2. El modelo de GP con BF preferido es capaz de capturar la dinámica intrínseca de la serie de precios, además de pronosticar con una mayor precisión que los reportados por la metodología ARIMA clásica y DAN2 para los horizontes de tiempo de 12 y 24 meses. Este resultado confirma que es posible la aplicación del algoritmo de GP a la predicción de la serie de precios promedio despachados en el mercado eléctrico colombiano con menor error y un nivel de variabilidad inferior que los modelos tradicionales de predicción de series de tiempo ARIMA y las redes neuronales dinámicas DAN2.

Referencias

[1] J. D. Velásquez, I. Dyner y R. C. Souza, ''¿Por qué es tan difícil obtener buenos pronósticos de los precios de la electricidad en mercados competitivos?'', Cuadernos de Administración, 20(34), 259-282, 2007.

[2] J. D. Velásquez H. y C. J. Franco C., ''Predicción de los precios de contratos de electricidad usando una red neuronal con arquitectura dinámica'', Innovar, vol.20, n.° 36, pp. 7-14. ISSN 0121-5051, 2010.

[3] M. Ghiassi y H. Saidane, ''A dynamic architecture for artificial neural networks'', Neurocomputing, 63, 397-413, 2005.

[4] G. E. P. Box y G. M. Jenkins, ''Time Series Analysis: Forecasting and Control'', San Francisco: Holden-Day Inc, 1970.

[5] J. R. Koza, ''Genetic Programming: On the Programming of Computers by Means of Natural Selection'', Cambridge: MIT Press, 1992.

[6] S. G. Makridakis, S. C. Wheelwright y R. J. Hyndman, ''Forecasting: Methods and applications (3a. ed.)'', New York: John Wiley & Sons, 1998.

[7] I. Dyner, C. J. Franco y S. Arango, ''El mercado mayorista de electricidad colombiano'', Medellín: Universidad Nacional de Colombia, 2008.

[8] C. A. Martínez y J. D. Velásquez H. ''Problemas abiertos en la aplicación de la Regresión Simbólica en el pronóstico de series de tiempo'', Tesis de maestría, Universidad Nacional de Colombia sede Medellín, 2011.