ARTÍCULOS
Memoria sobre el papel de Liouville en la historia de las funciones elípticas
Recollection of the role of Liouville
in the history of the elliptic functions
Leonardo Solanilla Chavarro*;
Ana Celi Tamayo Acevedo**;
Yefferson Palacios Mosquera***
*
Doctor en Matemáticas, Ph. D., Profesor asociado del Departamento de Matemáticas y Estadística, Facultad de Ciencias, Universidad del Tolima, Barrio Santa Elena, Ibagué, Tolima, Telefax: 098-2772049, leonsolc@ut. edu.co
** Matemática, Magister en Educación. Profesora asistente del Departamento de Ciencias Básicas, Universidad de Medellín, Carrera 87 N° 30 – 65, Medellín, Antioquia, Telefax: 094-3405598, actamayo@udem.edu.co
*** Magister en Educación Matemática, Profesor de Matemáticas, Institución Educativa Vida para Todo, Calle 45 N°10a-151, Medellín, Antioquia, Telefax: 094-3405598, yepm2@hotmail.com
Recibido:
03/04/2013
Aceptado: 06/09/2013
RESUMEN
Este artículo recoge las principales conclusiones de una investigación sobre las contribuciones de J. Liouville a la teoría contemporánea de las funciones elípticas. Cubre la mayor parte de los resultados de una colaboración entre el grupo SUMMA del Departamento de Ciencias Básicas de la Universidad de Medellín y el grupo Mat del Departamento de Matemáticas y Estadística de la Universidad del Tolima. El proyecto ha sido financiado parcialmente por la Vicerrectoría de Investigaciones de la Universidad de Medellín y la Facultad de Ciencias de la Universidad del Tolima. Comienza con una descripción de la circunstancia histórica de Liouville, luego de la emergencia del concepto moderno de función elíptica en los trabajos de Abel y Jacobi. Después se discuten ciertos pormenores de las Leçons impartidas por el célebre matemático francés en el año de 1847. Ellos cubren el teorema que hemos llamado de Liouville-Borchardt, las proposiciones fundamentales sobre el número de ceros de las funciones meromorfas doblemente periódicas y los resultados sobre la relación entre los ceros y los polos. Al final, se esbozan importantes conclusiones sobre el legado de Liouville a la teoría de las funciones elípticas de hoy.
PALABRAS CLAVE
historia de las matemáticas-siglo XIX, análisis complejo, funciones e integrales elípticas.
ABSTRACT
This paper collects the main conclusions of a research on the contributions of J. Liouville to the contemporary theory of the elliptic functions. It covers most of the results of a collaboration between the SUMMA group from the Universidad de Medellín Basic Sciences Department and the Mat group from the Universidad del Tolima Department of Mathematics and Statistics.
The project has been partially funded by the Universidad de Medellín Research Vice-Principal's Office and the Universidad del Tolima School of Sciences. It begins with a description of Liouville's historic background after the emergence of the elliptic function modern concept in the work of Abel and Jacobi. Subsequently, certain details of the Leçons chaired by the famous French mathematician in 1847 are discussed. Such details cover the so-called Liouville-Borchardt theorem, the fundamental propositions about the number of zeros of the meromorphic doubly periodic functions, and the results of the relation between the zeros and the poles. The end of the article outlines important conclusions regarding the Liouville's legacy to the current theory of the elliptic functions.
KEY WORDS
history of mathematics –19th century–, complex analysis, elliptic functions and integrals.
INTRODUCCIÓN
Con Liouville, las funciones elípticas se consumieron en el fuego de sus verdaderos fundamentos para resurgir renovadas, como ave fénix, en el nuevo rigor formal'' de las matemáticas del siglo XIX. Abel [1] y Jacobi [2] son, sin duda alguna, los padres de estas funciones. Sin embargo, es a Liouville a quien correspondió el honor de desvelarlas en toda su prístina belleza.
Las funciones elípticas de Abel y Jacobi, estudiadas en [3] y [4], constituían una materia intrincada, que no fluía fácilmente por descansar en las poderosas fórmulas de adición y en algunos hechos analíticos no muy claros. Ciertamente, en la década de 1820, se estudiaba el cálculo de las funciones complejas mediante los conocidos métodos de la variable real. Un completo resumen de estos hechos se puede hallar en [5].
Aproximadamente quince años después, el nueve de diciembre de 1844, Liouville realiza algunos comentarios a una memoria de Chasles. Ellos aparecen publicados en los Comptes Rendus à la Académie des Sciences de esta fecha. Allí se anuncia el descubrimiento de un nuevo método, muy simple por cierto, para estudiar las funciones elípticas. Sin embargo, en esta comunicación no hay detalles. Por ello, en este artículo, nos concentramos en las conferencias dictadas por Liouville [6] en París durante 1847, las cuales están documentadas en un artículo posterior. En ellas, se sientan las funciones elípticas sobre nuevas bases y se demuestran originales y poderosas propiedades, las cuales habían pasado desapercibidas para Abel y Jacobi.
Este artículo quiere estudiar dichas nuevas bases'' y propiedades a partir de las conferencias originales. Sin embargo, como suele pasar a veces en la historia humana, el camino no es tan directo como se podría pensar a primera vista: las mentadas Leçons de 1847 no vieron la luz sino hasta el año 1880 (ver [6]). C. W. Borchardt, amigo de Liouville, cuenta en este artículo de 1880 que, encontrándose de viaje en París durante 1847, fue invitado por el conferencista a escuchar sus hallazgos sobre las funciones doblemente periódicas. Sus apuntes estuvieron guardados durante treinta y tres largos años. Repentinamente (no sabemos con certeza por qué, tal vez por una lucha sobre la originalidad) decide publicarlas en el distinguidísimo Journal für Mathematik. Entre otras cosas, confiesa que cambió la demostración dada por Liouville al teorema fundamental, que los autores de este artículo nos hemos permitido bautizar como teorema de Liouville-Borchardt. El cambio no es, desde ningún punto de vista, ingenuo, como lo veremos en la sección siguiente.
A pesar de todas las dudas que surgen sobre las modificaciones que Borchardt realizó a sus anotaciones, hay razones para creerle y considerar que los hallazgos de Liouville en el año de 1847 valen. En verdad, nuestro interés principal no es el teorema fundamental en sí, sino sus corolarios para las funciones elípticas. No hay razón alguna que sugiera que dichos corolarios sufrieran retoques en su esencia durante los 33 años comprendidos entre las conferencias y su publicación.
Para lo que sigue, asumimos que el lector conoce los rudimentos de la variable compleja contemporánea. En la sección siguiente relatamos los sorprendentes resultados de Liouville y presentamos nuestra interpretación a la luz de las matemáticas de hoy. Luego, resumimos nuestra reflexión bajo la forma de conclusiones, las cuales aspiran a responder al título de este artículo. Es decir, ellas contienen la herencia que, en nuestro concepto, Liouville legó a la teoría contemporánea de las funciones elípticas. Invitamos al lector a mirar los originales y a consultar las investigaciones anteriores de nuestro grupo de trabajo, que aparecen citadas en las referencias bibliográficas. Veamos.
1. ELEMENTOS PARA UNA INTERPRETACIÓN
Decimos que una función 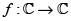 es elíptica si es meromorfa y doblemente periódica. Así pues, con el fin de simplificar la presentación y dado que Liouville [6] considera siempre funciones (meromorfas) doblemente periódicas, identificaremos en lo que sigue a las funciones elípticas con las funciones doblemente periódicas. Ciertamente, todas las funciones que consideraremos son meromorfas.
es elíptica si es meromorfa y doblemente periódica. Así pues, con el fin de simplificar la presentación y dado que Liouville [6] considera siempre funciones (meromorfas) doblemente periódicas, identificaremos en lo que sigue a las funciones elípticas con las funciones doblemente periódicas. Ciertamente, todas las funciones que consideraremos son meromorfas.
1.1. Diferenciación compleja
Hoy en día es, casi que universalmente, aceptado que la noción fundamental del cálculo complejo es aquella que es función holomorfa. Una función de valores complejos es holomorfa en un dominio complejo si es diferenciable en el sentido complejo en cada punto de dicho dominio. Este concepto permite una caracterización poderosísima para esta clase de funciones. A manera de ejemplo, tomamos el siguiente teorema de Remmert [7]:
Theorem. The following assertions about a continuous function 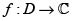 are equivalent:
are equivalent:
i) f is holomorphic (= complex-differentiable) in D.
ii) For every (compact) triangle 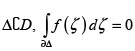 .
.
iii) f is locally integrable in D (the Morera condition).
iv) For every open disc B with 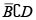
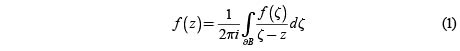
holds for every 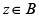 .
.
v) f is developable into a convergent power series around each point 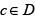 .
.
Para el estudio de las funciones elípticas es más pertinente la noción de función meromorfa. Una función es meromorfa en D si es holomorfa en el complemento de un conjunto discreto de D y tiene un polo en cada punto de dicho conjunto discreto.
Sin embargo, las cosas no siempre estuvieron tan claras. En las notas publicadas por Borchardt [6], aparece, tardíamente para ser ya el año de 1880, en lugar de una noción de función meromorfa, la siguiente descripción algo imprecisa
[...] soit f(z) une fonction bien déterminée, continue (c'est-à-dire qui ne passe pas brusquement d'une valeur finie à une autre qui en diffère d'une quantité finie) et telle que, pour les valeurs de zqui appartiennent aux points situés dans l'intérieur de la curve fermée K, elle prenne toutes les valeurs dont elle est susceptible pour des valeurs quelconques de z; cela posé [...]
Tampoco es cierto que las cosas se hayan aclarado de un día para otro. A lo largo del siglo XIX los matemáticos franceses no se ponían de acuerdo sobre la diferenciabilidad compleja y volvían una y otra vez a los conceptos que había establecido el barón de Cauchy al comienzo de este glorioso siglo. En el libro de texto de Briot y Bouquet [8] se lee, año 1859,
Ce premier Livre contient les principes d'une nouvelle théorie des fonctions.
Nous adoptons les définitions données par M. Cauchy...
[...] si la fonction u acquiert la même valeur au même point, quel que soit le chemin suivi pour y arriver, sans sortir de la portion considérée, M Cauchy dit que la fonction est monodrome dans cette portion du plan...
Lorsque la valeur de la dérivée est indépendante de la direction du déplacement, en d'autres termes lorsque la fonction admet une dérivée unique en chaque poin, M. Cauchy dit que la fonction es monogène...
M. Cauchy appelle fonction synectique une fonction qui reste finie, continue, monodrome et monogène dans toute l'entendue du plan. Par exemple, une fonction entière est une fonction synectique.
En 1880, el texto de Laurent [9] presenta el teorema integral de Cauchy de la siguiente manera:
Théorème De Cauchy. Le point z variant à l'intérieur d'un contour donné, si, à l'intérieur de ce contour, la fonction f(z) reste monodrome, monogène et finie, l'intégrale 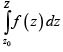 conservera toujours la même valeur, pourvu que le chemin qui mène de z0 à Z ne sorte pas du contour donné, quel que soit d'ailleurs ce chemin.
conservera toujours la même valeur, pourvu que le chemin qui mène de z0 à Z ne sorte pas du contour donné, quel que soit d'ailleurs ce chemin.
1.2. Teorema fundamental de Liouville-Borchardt
Liouville sin duda conocía las construcciones fundacionales de Abel [1] y Jacobi [2]. Por ello, sabía que las funciones elípticas, en cuanto doblemente periódicas, quedaban determinadas por su comportamiento en un paralelogramo fundamental. Más aún, este paralelogramo se puede escoger de tal manera que su frontera no contenga las singularidades aisladas de la función. Así, el problema se reduce a estudiar el comportamiento de las funciones meromorfas en la región encerrada por, digamos, una curva de Jordan regular a trozos. Tal es el asunto que resuelve el teorema de Liouville-Borchardt: si f(z) es meromorfa en la cerradura de una región encerrada por una tal curva K,
je dis qu'il y aura au moins une valeur de z, située dans l'intérieur de K, pour laquelle 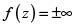 , à moins que f(z) ne soit = constante.
, à moins que f(z) ne soit = constante.
Ver [6]. La demostración de 1880 se basa en un resultado analítico de Cauchy. No olvidemos que Borchardt confiesa que esta no fue la prueba original de Liouville. Todo parece que el teorema original de 1847 era mucho menos general y se basaba en el desarrollo de una función elíptica en series trigonométricas complejas.
La primera reacción del lector contemporáneo es la de relacionar este resultado con lo que hoy se llama teorema de Liouville: toda función entera, es decir, holomorfa en todo el plano 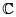 , acotada es constante. A pesar de la similitud, la relación no es, desde ningún punto de vista, trivial. Para ello, basta recordar el célebre teorema de la aplicación de Riemann, que afirma que ni el plano complejo ni la esfera son conformemente equivalentes a la región encerrada por la curva K. Una explicación más detallada de estos hechos puede consultarse en las conclusiones del trabajo de Palacios [10]. A propósito, entre otras interpretaciones posibles, en el primer capítulo de [10] se propone que el teorema de Liouville-Borchardt se podría formular en lenguaje contemporáneo bajo la siguiente forma.
, acotada es constante. A pesar de la similitud, la relación no es, desde ningún punto de vista, trivial. Para ello, basta recordar el célebre teorema de la aplicación de Riemann, que afirma que ni el plano complejo ni la esfera son conformemente equivalentes a la región encerrada por la curva K. Una explicación más detallada de estos hechos puede consultarse en las conclusiones del trabajo de Palacios [10]. A propósito, entre otras interpretaciones posibles, en el primer capítulo de [10] se propone que el teorema de Liouville-Borchardt se podría formular en lenguaje contemporáneo bajo la siguiente forma.
Teorema de Liouville-Borchardt (versión de hoy). Sea 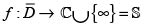 (esfera de Riemann) una función meromoria no constante definida en la clausura de un dominio
(esfera de Riemann) una función meromoria no constante definida en la clausura de un dominio  del plano complejo. Si
del plano complejo. Si 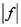 no se hace infinita en
no se hace infinita en 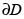 , ni alcanza allí su valor máximo, entonces existe un punto
, ni alcanza allí su valor máximo, entonces existe un punto 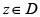 tal que
tal que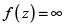 .
.
En fin, toda la teoría de Liouville para las funciones elípticas se desprende de aquí. Pasemos, pues, a sus corolarios o consecuencias. Comprenden cuatro teoremas y lema.
Veamos.
1.3. Número de polos de una función elíptica
La primera consecuencia del teorema de Liouville-Borchardt salta inmediatamente a la vista.
Primer teorema de Liouville para las funciones elípticas. Una función elíptica debe tener al menos un polo en su paralelogramo fundamental (a menos de que sea trivial, o sea, constante).
De nuevo, los lectores contemporáneos defenderán que esto se puede probar más fácilmente con ayuda del mencionado teorema de Liouville, al tomar a todo 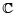 como dominio de la función elíptica, y suponer la inexistencia de polos. Los caminos recorridos a lo largo de la historia no han sido siempre los más cortos.
como dominio de la función elíptica, y suponer la inexistencia de polos. Los caminos recorridos a lo largo de la historia no han sido siempre los más cortos.
A propósito del teorema de Liouville, en el transcurso de esta investigación hemos descubierto que, a lo largo de toda su vida, el gran matemático francés dio al menos tres versiones del resultado que lleva su nombre. El lector interesado en los avatares de esta famosa proposición puede referirse al interesante artículo de Peiffer [11].
Menos evidente es el siguiente resultado encontrado por Liouville.
Segundo teorema de Liouville para las funciones elípticas. Una función elíptica con un polo único en su paralelogramo fundamental es trivial, o sea, constante.
Para demostrar este hecho, se procede por contradicción. Si la función tiene un solo polo α, entonces la parte principal de su serie de Laurent tiene la forma
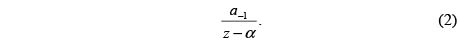
De esta manera, por medio de ingeniosas manipulaciones algebraicas y como consecuencia de la doble periodicidad, se llega a una contradicción con lo dicho en el primer teorema de Liouville. En este punto, invitamos al lector a consultar los detalles en [6] y [10].
Y, ¿qué pasará entonces con las funciones elípticas con dos polos? Pues esta pregunta ya tenía una respuesta en la época de Liouville. Abel [1] y Jacobi [2] ya habían construido funciones elípticas con dos polos mediante el conocido procedimiento de inversión formal de una función integral elíptica, cf. [5]. Sin embargo, Liouville [6] se siente obligado a mostrar una manera más sencilla de construirlas mediante funciones trigonométricas complejas.
Y llega mucho más lejos.
Tercer teorema de Liouville para las funciones elípticas. Existen funciones elípticas con dos polos. Aún más, dados números complejos 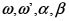 es posible construir una función elíptica que tenga periodos
es posible construir una función elíptica que tenga periodos 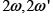 y polos
y polos 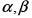 . Si llamamos
. Si llamamos 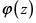 a dicha función, entonces todas las funciones elípticas con los mismos periodos y los mismos polos son combinaciones lineales de la forma
a dicha función, entonces todas las funciones elípticas con los mismos periodos y los mismos polos son combinaciones lineales de la forma
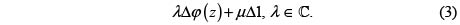
En este caso la demostración es directa. Se parte de la parte principal
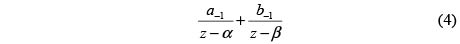
de la función elíptica con los mismos periodos y polos que 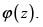 El primer teorema implica entonces que dicha función es una combinación lineal de la forma buscada. Los pormenores aparecen en [6] y [10].
El primer teorema implica entonces que dicha función es una combinación lineal de la forma buscada. Los pormenores aparecen en [6] y [10].
1.4. Relación entre ceros y polos
Al lado de los teoremas de Liouville, el artículo fundacional [6] desarrolla toda una teoría que alberga también consecuencias muy importantes para la mejor comprensión de las funciones elípticas, en particular, para el entendimiento de sus gráficas. Como este asunto no constituye la materia primordial de esta presentación, ponemos todos los resultados juntos en el siguiente lema, que presentamos sin demostración. A los interesados en el tema, les recomendamos el artículo original [6], así como las interpretaciones de Palacios [10].
Lema de Liouville sobre los ceros de una función elíptica. Una función elíptica con dos polos distintos 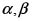 tiene exactamente dos ceros distintos a,b. Además, En este caso, se verifica que
tiene exactamente dos ceros distintos a,b. Además, En este caso, se verifica que
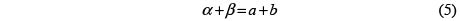
donde la suma se lleva a cabo sin salirse de un paralelogramo fundamental. Es decir, se trata de la adición módulo el retículo 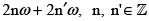 .
.
Son estos resultados sobre la relación de los polos y los ceros los que llevan a Liouville a descubrir propiedades algebraicas más generales en los espacios de funciones elípticas.
Cuarto teorema de Liouville para las funciones elípticas. Si 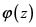 es una función elíptica con periodos
es una función elíptica con periodos 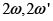 , entonces cualquier otra función con esta propiedad (mismos periodos, sin importar donde se sitúen sus polos o sus ceros) se puede escribir como una función racional de
, entonces cualquier otra función con esta propiedad (mismos periodos, sin importar donde se sitúen sus polos o sus ceros) se puede escribir como una función racional de 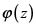 .
.
1.5. Funciones elípticas con más de dos polos
Los teoremas y el lema enunciados hasta este punto yacen en la base de la teoría actual de las funciones elípticas; compárese, por ejemplo, con Lang [12]. No obstante, es nuestro deber aclarar que los descubrimientos de Liouville [6] son mucho más generales porque cubren el caso de funciones con más de dos polos.
Sus conclusiones son muy sencillas y elegantes. En verdad, la sección cuarta del artículo [6] comienza con el siguiente párrafo.
Les fonctions doublement périodiques à deux infinies ne sont pas seulement les plus simples fonctions de ce genre, mais elles forment en même temps les éléments, dont se composent algébriquement les fonctions doublement périodiques à plusieurs infinis.
Ciertamente, a partir de este punto Liouville se encarga de mostrar la manera como las funciones elípticas de más de dos polos se pueden expresar como sumas o productos de las más simples, es decir, de aquellas con dos polos. De paso, prueba que el número de ceros de las funciones generales es igual al número de sus polos. Además, se tiene que la suma de todos los ceros iguala a la suma de todos los polos, módulo el retículo fundamental, naturalmente. Ver [6] y [10] para mayores explicaciones.
2. CONCLUSIONES
2.1. Legado de Liouville
A pesar de que Liouville no tenía a su disposición todo el formalismo contemporáneo de la variable compleja, supo descubrir que este campo de las matemáticas era el axioma fundamental de las funciones elípticas. Después de él, la teoría de estas funciones se ha convertido en un capítulo más de la variable compleja.
En otras palabras, la principal conclusión de este trabajo es que Liouville descubrió un conjunto de supuestos o hipótesis, a partir de los cuales la teoría de las funciones elípticas discurre con gran simplicidad y elegancia. Dicho conjunto de supuestos es, sencillamente, la teoría de las funciones meromorfas. Basta, ciertamente, comparar los dificilísimos e intrincados procedimientos de Abel [1] y Jacobi [2] con la recatada elegancia de Liouville [6] para darse cuenta del tremendo avance que representó en la historia de la disciplina la colocación de la variable compleja en la base de las funciones elípticas. Y no se trata solamente de un asunto de elegancia y simplificación, sino también de contenido: los nuevos métodos permitieron demostrar rigurosamente los cuatro teoremas de Liouville para las funciones elípticas, unos resultados que Abel [1] y Jacobi [2] no pudieron establecer, a pesar de tener ciertas intuiciones sobre ellos.
2.2. Formalismo matemático
En relación con la conclusión anterior, se debe señalar que el proceder de Liouville enseña o muestra una nueva forma de construir una teoría matemática (es precisamente esto lo que hace interesante la mirada histórica a los textos originales, pues allí se revelan las nuevas creaciones). En la base, yacen los axiomas, que, en este caso, son las propiedades de las funciones meromorfas que desvela el teorema de Liouville-Borchardt. Se trata de un comienzo duro, porque es allí donde yace la componente analítica de la teoría de Liouville para las funciones elípticas. Insistimos que es un punto de partida duro o difícil porque descansa, en el fondo, sobre el principio del módulo máximo de la variable compleja, una proposición que demanda gran domino del análisis. Después de superarlo, todo fluye con rapidez y simplicidad. Con esto queremos decir que, una vez establecido el teorema fundamental de Liouville-Borchardt, los cuatro teoremas y el lema de Liouville se prueban mediante procedimientos algebraicos y topológicos muy simples. Bueno, la topología merece unas explicaciones adicionales, ya que no se conocía en la época de las Leçons (1847). Sin embargo, los matemáticos de hoy reconocen que las formulaciones de Liouville admiten una interpretación más sencilla si se introduce la topología moderna. Véase, por ejemplo, la versión del teorema de Liouville-Borchardt propuesta en [10].
Para dejar en claro las cosas de una buena vez, es notable la influencia e importancia del álgebra moderna que nacía en la primera mitad del siglo XIX. Así lo prueba, además, el deseo de Liouville por descubrir propiedades (hoy diríamos estructuras) algebraicas para ciertos conjuntos de funciones elípticas. Nos referimos concretamente a los teoremas tercero y cuarto, que se enmarcan dentro de lo que, hoy en día, llamaríamos un cuerpo de funciones. También se nota este espíritu algebraico en la consideración de las series de Laurent, en cuanto formadas por una parte entera o de Taylor y una parte fraccionaria o principal.
En concreto, todo indica que en Liouville [6] se manifiesta una fuerte tendencia a concebir las matemáticas como una teoría de la formas del pensamiento. Nos referimos con esto a la concepción de las matemáticas documentada por Schubring en las conclusiones de [13], una obra de carácter histórico que estudia extensivamente el devenir del análisis durante los siglos XVII al XIX en Francia y Alemania.
2.3. Estilo de Liouville, rigor analítico
Todo indica que la divulgación científica de los resultados de la teoría de las funciones elípticas ha preferido siempre la senda del álgebra, en lugar que la del análisis. Este tema ya ha sido tratado en [14] para la emergencia de las funciones elípticas. Aunque no se puede negar la esencia analítica del tema, tanto Abel [1] y Jacobi [2] como Liouville [6] optaron por salir muy rápidamente de los fundamentos analíticos para explorar algebraicamente sus consecuencias.
Recordemos que el análisis vivió toda una revolución como consecuencia de la revisión realizada por Cauchy a los fundamentos del cálculo infinitesimal. El cambio defendía una gran coherencia interna entre definiciones, teoremas y demostraciones. Esta visión se oponía a la aproximación intuitiva de lo infinitamente pequeño'', predominante desde el siglo XVII. La revisión o revolución de Cauchy, a la que nos referimos, está documentada ampliamente en muchas investigaciones sobre la historia del análisis. Por ejemplo, [13] contiene una descripción muy completa de las querellas analíticas ocurridas en Francia y Alemania durante varios siglos. Un trabajo más focalizado es el objeto de la tercera parte de [15], donde se explicita el sentimiento de inconformidad de Abel frente al análisis de su época, al que consideraba carente de rigor y sistematización.
Respecto a este nuevo rigor analítico'' de la primera mitad del siglo XIX, nos inclinamos a tildar el estilo de Liouville [6] como mixto. En verdad, por un lado no se puede negar que sus descubrimientos descansan sobre los estudios de Cauchy en torno a la diferenciabilidad compleja, o sea, en la fuente misma del nuevo rigor''. De otro lado, es indudable que las Leçons de 1847 están concebidas y dispuestas como una máquina de deducción formal, consciente del álgebra de su época y seminconsciente de los asuntos topológicos.
El Joseph Liouville de [6] es, ya casi, un matemático de nuestros días.
3. AGRADECIMIENTOS
De manera muy especial, los autores manifiestan su deuda con el profesor Gabriel Pareja Ocampo, de la Universidad de Medellín, cuya participación en nuestro grupo de trabajo es permanente e imprescindible. Los autores agradecen también el cordial apoyo financiero de la Facultad de Ciencias de la Universidad del Tolima y la Vicerrectoría de Investigaciones de la Universidad de Medellín.
REFERENCIAS
[1] N. H. Abel, ''Recherches sur les fonctions elliptiques, '' Journal für die reine und angewandte Mathematik, vol. 2, pp. 263-388, 1827.
[2] C. G. J. Jacobi, Fundamenta nova theoriae functionum ellipticarum, Regiomonti: Bornträger, 1929, p. 191.
[3] J. G. Murcia y A. Saldaña, Funciones elípticas de Abel, Ibagué, Tolima: Universidad del Tolima, 2011, p. 44.
[4] L. Solanilla, Las transformaciones elípticas de Jacobi, Ibagué, Tolima: Universidad del Tolima, 2012, p. 69.
[5] G. Pareja, L. Solanilla y A. C. Tamayo, ''Memoria sobre la emergencia de las funciones elípticas,'' artículo en proceso de publicación, 2012.
[6] J. Liouville, ''Leçons sur les fonctions doublement périodiques faites en 1847 par M. J. Liouville, ''Journal für die reine und angewandte Mathematik, vol. 88, pp. 277-310, 1880.
[7] R. Remmert, Theory of Complex Functions, New York: Springer, 1991, p. 453.
[8] M. Briot et M. Bouquet, Théorie des fonctions doublement périodiques et, en particulier, des fonctions elliptiques, Paris: Mallet-Bachelier, 1859, p. 342.
[9] H. Laurent, Théorie élémentaire des fonctions elliptiques, Paris: Gauthier-Villars, 1880, p. 184.
[10] Y. Palacios, Contribuciones de Liouville a las funciones elípticas, Medellín: Universidad de Medellín, Departamento de Ciencias Básicas, Programa de Maestría en Educación Matemática, 2013, p. 50.
[11] J. Peiffer, ''Joseph Liouville (1809-1882): ses contributions à la théorie des fonctions d'une variable complexe,'' Revue d'histoire des sciences, vol. 36, n.° 3- 4, 209-238.
[12] S. Lang, Elliptic Functions, New York: Springer, 1987, p. 326.
[13] G. Schubring, Conflicts between Generalization, Rigor, and Intuition. Number Concepts Underlying the Development of Analysis in 17–19th Century. France and Germany, New York: Springer, 2005, p. 678.
[14] G. Pareja, L. Solanilla y A. C. Tamayo, ''Indicios del papel preponderante del Álgebra en la emergencia de las funciones elípticas, ''Revista Facultad de Ciencias Universidad Nacional de Colombia, Sede Medellín, vol. 2, n.° 2, pp. 43 -52, 2013.
[15] H. K. Sørensen, The Mathematics of Niels Henrik Abel: Continuation and New Approaches in Mathematics During the 1820s, Department of Science Studies, University of Aarhus, Denmark: 2010, p. 437.
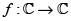 es elíptica si es meromorfa y doblemente periódica. Así pues, con el fin de simplificar la presentación y dado que Liouville [6] considera siempre funciones (meromorfas) doblemente periódicas, identificaremos en lo que sigue a las funciones elípticas con las funciones doblemente periódicas. Ciertamente, todas las funciones que consideraremos son meromorfas.
es elíptica si es meromorfa y doblemente periódica. Así pues, con el fin de simplificar la presentación y dado que Liouville [6] considera siempre funciones (meromorfas) doblemente periódicas, identificaremos en lo que sigue a las funciones elípticas con las funciones doblemente periódicas. Ciertamente, todas las funciones que consideraremos son meromorfas.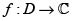 are equivalent:
are equivalent: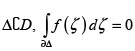 .
.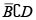
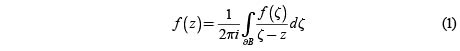
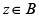 .
.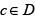 .
.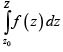 conservera toujours la même valeur, pourvu que le chemin qui mène de z0 à Z ne sorte pas du contour donné, quel que soit d'ailleurs ce chemin.
conservera toujours la même valeur, pourvu que le chemin qui mène de z0 à Z ne sorte pas du contour donné, quel que soit d'ailleurs ce chemin.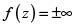 , à moins que f(z) ne soit = constante.
, à moins que f(z) ne soit = constante.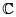 , acotada es constante. A pesar de la similitud, la relación no es, desde ningún punto de vista, trivial. Para ello, basta recordar el célebre teorema de la aplicación de Riemann, que afirma que ni el plano complejo ni la esfera son conformemente equivalentes a la región encerrada por la curva K. Una explicación más detallada de estos hechos puede consultarse en las conclusiones del trabajo de Palacios [10]. A propósito, entre otras interpretaciones posibles, en el primer capítulo de [10] se propone que el teorema de Liouville-Borchardt se podría formular en lenguaje contemporáneo bajo la siguiente forma.
, acotada es constante. A pesar de la similitud, la relación no es, desde ningún punto de vista, trivial. Para ello, basta recordar el célebre teorema de la aplicación de Riemann, que afirma que ni el plano complejo ni la esfera son conformemente equivalentes a la región encerrada por la curva K. Una explicación más detallada de estos hechos puede consultarse en las conclusiones del trabajo de Palacios [10]. A propósito, entre otras interpretaciones posibles, en el primer capítulo de [10] se propone que el teorema de Liouville-Borchardt se podría formular en lenguaje contemporáneo bajo la siguiente forma.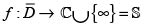 (esfera de Riemann) una función meromoria no constante definida en la clausura de un dominio
(esfera de Riemann) una función meromoria no constante definida en la clausura de un dominio  del plano complejo. Si
del plano complejo. Si 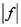 no se hace infinita en
no se hace infinita en 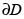 , ni alcanza allí su valor máximo, entonces existe un punto
, ni alcanza allí su valor máximo, entonces existe un punto 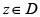 tal que
tal que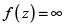 .
.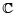 como dominio de la función elíptica, y suponer la inexistencia de polos. Los caminos recorridos a lo largo de la historia no han sido siempre los más cortos.
como dominio de la función elíptica, y suponer la inexistencia de polos. Los caminos recorridos a lo largo de la historia no han sido siempre los más cortos.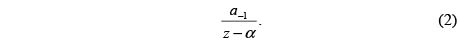
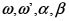 es posible construir una función elíptica que tenga periodos
es posible construir una función elíptica que tenga periodos 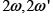 y polos
y polos 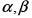 . Si llamamos
. Si llamamos 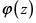 a dicha función, entonces todas las funciones elípticas con los mismos periodos y los mismos polos son combinaciones lineales de la forma
a dicha función, entonces todas las funciones elípticas con los mismos periodos y los mismos polos son combinaciones lineales de la forma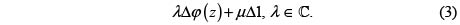
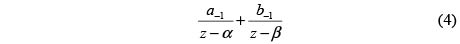
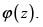 El primer teorema implica entonces que dicha función es una combinación lineal de la forma buscada. Los pormenores aparecen en [6] y [10].
El primer teorema implica entonces que dicha función es una combinación lineal de la forma buscada. Los pormenores aparecen en [6] y [10].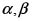 tiene exactamente dos ceros distintos a,b. Además, En este caso, se verifica que
tiene exactamente dos ceros distintos a,b. Además, En este caso, se verifica que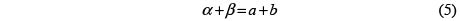
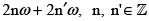 .
.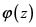 es una función elíptica con periodos
es una función elíptica con periodos 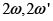 , entonces cualquier otra función con esta propiedad (mismos periodos, sin importar donde se sitúen sus polos o sus ceros) se puede escribir como una función racional de
, entonces cualquier otra función con esta propiedad (mismos periodos, sin importar donde se sitúen sus polos o sus ceros) se puede escribir como una función racional de 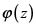 .
.