ARTÍCULOS
Modelo de selección de portafolio óptimo de acciones mediante el análisis de Black–Litterman
Optimal portfolio selection model using Black–Litterman analysis
Laura Giraldo Cárdenas*; John Malver Díaz Zapata**; Sandra Milena Arboleda Ríos***; Cindy Lucia Galarcio Padilla****; Jorge Enrique Lotero Botero*****; Felipe Isaza Cuervo******
* Especialista en Finanzas y Mercado de Capitales, Universidad de Medellín. Coordinadora de Operaciones, Compañía de Financiamiento Tuya S. A. e–mail: lgiraldocardenas@hotmail.com
** Especialista en Finanzas y Mercado de Capitales, Universidad de Medellín. Analista de Parámetros, Compañía de Financiamiento Tuya S. A. e–mail: malver18@yahoo.com
*** Especialista en Finanzas y Mercado de Capitales, Universidad de Medellín. Tesorera, Bananeras de Urabá S. A. e–mail: smarboledar@hotmail.com
**** Especialista en Finanzas y Mercado de Capitales, Universidad de Medellín. Analista contable, La Soberana S. A. e–mail: cindygalarcio@gmail.com
***** Magíster en Ingeniería Administrativa, Universidad Nacional, especialista en Finanzas, EAFIT, ingeniero industrial, Universidad Nacional. e–mail: jelotero@une.net.co
****** Doctor en Ingeniería – Industria y Organizaciones; máster en Ingeniería Administrativa, Universidad Nacional. Docente tiempo completo Ingeniería Financiera e investigador del Grupo de Investigaciones en Finanzas – GINIF y del Grupo de Investigación en Energía GRINEN de la Universidad de Medellín. e–mail: fisaza@udem.edu.co
Recibido: 20/05/2015
Aceptado: 10/07/2015
RESUMEN
Dentro de las diversas teorías financieras que se enfocan en la asignación óptima de recursos en un portafolio de inversión, la propuesta de Black–Litterman es la única que incorpora las expectativas futuras que tienen los inversionistas sobre los activos en los cuales destinarán sus recursos. En este trabajo se presenta la propuesta de Black–Litterman como una herramienta para mejorar la selección óptima de portafolios y como un insumo que mejora la estructuración de portafolios a través del modelo clásico propuesto por Markowitz. Además de la presentación teórica del modelo de Black–Litterman, se realiza un análisis de caso estructurando un portafolio óptimo sobre el índice COLCAP del mercado de valores colombiano. Además de permitir incorporar las visiones de los inversionistas, los resultados obtenidos mediante Black–Litterman ayudan a crear mejores portafolios de inversión a través del modelo de Markowitz, tanto en maximización de rendimientos como de minimización de varianza.
PALABRAS CLAVE: Riesgo, Black–Litterman, gestión de portafolios
ABSTRACT
Among the several financial theories related with the optimal portfolio selection, Black–Litterman proposal is the only one that considers the future expectation of investors over the assets that are being considered in the portfolio allocation problem. This works presents the Black–Litterman portfolio proposal as a tool that improves the optimal portfolio selection and also shows how the results obtained with this model could be used as an input to the classical Markowitz portfolio selection model. Besides the theorical presentation of the Black–Litterman portfolio model, a portfolio analysis over the COLCAP index in the Colombian Capital Market is presented, in this case the expectations of investors are taking into account and the results obtained from the Black–Litterman model are used to improve an optimal portfolio that consider the previous expectations under the Markowitz portfolio selection model, either under minimum variance and maximum return optimization.
KEY WORDS: Risk, Black–Litterman model, portfolio management
INTRODUCCIÓN Y PLANTEAMIENTO DEL PROBLEMA
La creación de un portafolio eficiente según los postulados de Markowitz [1] se basa en la idea de lograr un equilibrio entre rendimiento y riesgo, entendiéndose el riesgo como la volatilidad de los rendimientos de algún instrumento de inversión. La metodología propuesta por Markowitz es uno de los pilares fundamentales de las finanzas modernas, y permite a los agentes de mercado determinar de manera eficiente portafolios de inversión en los cuales destinan sus excedentes de liquidez. Este trabajo presenta un análisis de las diferentes propuestas de la teoría financiera mediante las cuales se ha estudiado el problema de estructuración y selección de portafolios, haciendo énfasis en la propuesta de Black–Litterman, BL [2]. El aporte de la propuesta de BL incorpora el supuesto que los individuos no solo toman decisiones basadas en los rendimientos históricos de los instrumentos financieros, sino en las expectativas sobre los rendimientos futuros que estos tienen sobre dichos instrumentos, y con base en estas imágenes o expectativas complementan la información que les brinda el estudio histórico del activo y toman sus decisiones de inversión.
Este trabajo describe la propuesta de BL de manera que los agentes de mercado puedan utilizarla para gestionar portafolios óptimos, minimizando el riesgo y maximizando los rendimientos esperados, a la vez que permite incluir variables dinámicas en el modelo de selección. En la aplicación de este modelo es importante considerar su pertinencia actual, pues las tendencias de los mercados bursátiles muestran que estos cada día están más inmersos en el proceso de la globalización, lo que representa para el inversionista una enorme oportunidad para diversificar sus productos financieros; es por esta razón que la aplicación del modelo de BL permitirá al inversionista identificar los elementos que afectan su portafolio de inversión dentro de los mercados globales. Este trabajo, además, busca divulgar la aplicación del modelo de BL, por lo que puede ser utilizado como una fuente de referencia teórica y práctica; también puede aplicarse en un mercado emergente como el colombiano, caracterizado por una alta volatilidad e incertidumbre frente a las expectativas futuras del rendimiento de los activos.
Este trabajo se organiza de la siguiente manera: el numeral 2 presenta una revisión de literatura relacionada con los aspectos teóricos que definen la teoría moderna de selección de portafolios; el numeral 3 describe el modelo de Black–Litterman aplicado a la selección de portafolios óptimos; el numeral 4 presenta la aplicación del modelo BL a un caso que toma activos del mercado colombiano y finalmente el numeral 5 presenta las conclusiones.
1 REVISIÓN DE LITERATURA PORTAFOLIO DE INVERSIÓN
Los portafolios de inversión pueden remontarse al estudio de Markowitz [1], donde se condiciona la composición de un portafolio de inversión al concepto de minimización del riesgo. En su modelo, Markowitz proporciona alternativas para el inversionista que quiere obtener la máxima rentabilidad sin someterse al nivel más elevado de riesgo, así como diseñar una cartera óptima para disminuir el riesgo sin afectar la rentabilidad esperada. El modelo de Markowitz [1] se plantea como la minimización del riesgo, sujeto a la función de rentabilidad y se presenta de la siguiente forma:
Sujeto a:
Donde xi es la proporción del presupuesto del inversionista destinado al activo i y corresponde con la incógnita del programa de optimización;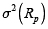 
es la varianza del portafolio p, y σij, la covarianza entre los rendimientos de los activos financieros i y j; E(Rpij), es la rentabilidad del portafolio p, de tal forma que al variar el parámetro V* obtendremos en cada caso el conjunto de proporciones xi que minimizan el riesgo de la cartera, así como su valor correspondiente. El conjunto de pares 
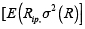o combinaciones rentabilidad–riesgo de todas las carteras eficientes es denominado ''frontera eficiente''. Una vez conocida esta, el inversionista, de acuerdo con sus preferencias de riesgo, elegirá su cartera óptima [3].
Por su parte, Tobin [4] considera una cartera de activos financieros en la que el dinero es una reserva de valor segura, pero que no otorga rendimientos futuros, mientras que otros activos, como bonos y acciones, sí brindan rendimientos, pero, a su vez, llevan implícito un riesgo, el cual se espera que se vea compensado con un mayor rendimiento esperado futuro, y donde la expectativa de retorno es proporcional al riesgo percibido: mayor riesgo implica mayor expectativa de rentabilidad. Tobin formula un marco optimizador en el cual la demanda de dinero sale de las decisiones de maximizar una función de utilidad en la que los individuos están afectados no solo por el retorno esperado sino también por el riesgo de la cartera, y en la cual el agente debe elegir una combinación de activos, dadas su riqueza disponible para invertir, sus preferencias y el costo de oportunidad.
Sharpe [5], tomando como punto de partida los trabajos de Markowitz y Tobin, desarrolló el modelo de Capital Asset Pricing Model (CAPM), el cual permite calcular el precio de un activo o una cartera de inversión. Para esto propone el uso de la recta Línea de Mercado de Capitales (SML) que representa el retorno esperado de todos los activos del mercado como función del riesgo no diversificable y su relación con el retorno del mercado y el riesgo sistémico (β). Ross [6] propone el modelo APT (Abitrage Pricing Theory), que es una propuesta similar al CAPM pero de carácter multivariado donde el rendimiento de los activos considera, además del rendimiento del mercado, otros factores de riesgo.
De la década del noventa, se destacan trabajos como la propuesta de Artzner et al [7], quienes analizan los niveles de riesgo aceptable, definiendo el riesgo como una variable que fluctúa de acuerdo con el valor futuro de una posición para sus diferentes estados de la naturaleza. En la propuesta de Zhang, Xiao y Wang [8] se sustituyen los conceptos de media y varianza probabilística utilizados por Markowitz por el de media y varianza provenientes de un conjunto de números difusos, generando así un escenario más favorable para la selección de inversiones bajo incertidumbre.
El modelo propuesto por Black y Litterman [2] surge como un avance en la teoría de Markowitz la cual se basa principalmente en el desempeño histórico de los activos analizados sin considerar las expectativas e información que tiene el inversionista sobre el futuro. El principal aporte del modelo BL es la inclusión de las expectativas de los inversionistas, las cuales son tenidas en cuenta en la elección óptima del portafolio. Las características particulares del modelo BL serán explicadas con mayor detalle en el numeral 3. Buenaventura y Cuevas [9] hacen una propuesta metodológica para la optimización de portafolios de inversión a partir de la teoría de Markowitz [1] y la maximización de la pendiente de la Línea de Mercado de Capitales. Becerra y Melo [10] describen las medidas de dependencia de las variables del portafolio, y presentan la cópula como una estructura flexible que permite caracterizar, diferentes, dichas dependencias; en este caso la cópula es una función que aproxima el comportamiento de variables aleatorias a partir de sus comportamientos individuales. La selección de un portafolio óptimo puede no estar correlacionada con el análisis del riesgo asociado a cada uno de los instrumentos que la conforman. Por ejemplo Castillo y Lama [11] suponen que la existencia de un portafolio óptimo determina el ''Teorema de Separación'', según el cual el inversionista puede realizar una selección óptima sin tener conocimiento de las preferencias hacia el riesgo del inversionista, limitar la decisión a la elaboración de una frontera eficiente y elegir la combinación de instrumentos que se encuentran allí; así logra una aplicación directa de la teoría de Markowitz [1].
Con relación a aplicaciones en Latinoamérica, Cruz, Urrutia y Medina [12] desarrollan un modelo dual que permite maximizar la rentabilidad y minimizar la inversión inicial requerida, mientras que Cruz y Clement [13], con relación a la apertura de la inversión hacia mercados globales, afirman que uno de los riesgos que debe tener en cuenta el inversionista al incursionar en dichos mercados es el riesgo cambiario, dado que el rendimiento no solo dependerá de la variación en precios del activo a invertir, sino también de la evolución de la moneda en su tasa cambiaria, por lo cual se hace necesario hacer un estudio que permita administrar de manera eficiente estos riesgos recomendando el uso del modelo BL para la administración de los riesgos de los portafolios internacionales o globales. Las características de las cuatro principales propuestas teóricas para la estructuración de portafolios se resumen en la tabla 1.
2 DESCRIPCIÓN DEL MODELO DE SELECCIÓN DE PORTAFOLIOS DE ACUERDO CON LA PROPUESTA DE BLACK–LITTERMAN
El modelo de Black–Litterman como versión mejorada del modelo Markowitz considera los siguientes aspectos: en el mercado existen n activos, con capitalizaciones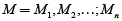 
y donde la capitalización de mercado es igual al número de títulos o unidades del activo disponibles en el mercado por su respectivo precio. Las ponderaciones de mercado de los n activos están dadas por el vector 
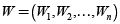en donde la ponderación del activo i es:
El coeficiente de aversión al riesgo del inversionista (δ), el cual es constante, se determina de la siguiente forma:
Donde es el retorno esperado del mercado, Rf es la tasa libre de riesgo y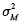 
es la varianza del retorno del mercado, el exceso de retornos implícitos de equilibrio (Π) se puede expresar como sigue:
Estos retornos se llaman Retornos Implícitos de Equilibrio, debido a que si los precios de los activos se ajustan hasta los retornos esperados, estos serán iguales a lo que creen los inversionistas, haciendo la suposición de que en general se tiene la misma expectativa de mercado; dichos ajustes hacen que la demanda iguale la oferta.
El modelo BL utiliza la aproximación bayesiana para la inferencia de los retornos esperados de los activos del portafolio. Este enfoque hace que a los rendimientos esperados se les pueda inferir su distribución de probabilidad con base en las creencias o expectativas previas que se tengan sobre la evolución de los activos que conformarían el portafolio y los rendimientos esperados de un portafolio inicial, el cual se obtiene mediante un modelo CAPM, de Markowtz o un índice de mercado.
Suponiendo que existen N activos en el mercado, que pueden incluir acciones, bonos, divisas y otros activos, los rendimientos de estos activos tienen una distribución normal donde μ es el rendimiento esperado y Σ la correspondiente matriz de covarianza; con base en esto el retorno de los activos en su conjunto se asume que sigue una distribución normal con parámetros μ y Σ; así
Donde r es el vector de los rendimientos de los activos. Si se asume que todos los inversionistas tienen la cartera de mercado Weq, y en donde las primas de riesgo de equilibrio Π son tales que si todos los inversionistas tienen el mismo punto de vista, la demanda de estos activos es exactamente igual a la oferta [7]. Suponiendo que la tolerancia al riesgo es representado por el parámetro de aversión al riesgo δ, las primas de riesgo de equilibrio se estiman como:
El modelo bayesiano previo implica que los retornos esperados μ se ubiquen en los valores de equilibrio, distribuyéndose normalmente con la media de Π:
Donde ε(e) es un vector aleatorio con distribución normal con media cero y matriz de covarianza τ Σ, donde τ es una escala que indica la incertidumbre del portafolio inicial. Además del portafolio inicial, el inversionista también tiene una serie de puntos de vista sobre los rendimientos del mercado en donde el inversionista tiene un conjunto de K opiniones sobre el rendimiento de los instrumentos del portafolio. Las opiniones se expresan en términos del retorno esperado de un portafolio pK, la cual distribuye normalmente con media qK qk y desviación estándar ωk. De esta manera P es una matriz que selecciona los instrumentos del portafolio sobre los cuales se forma una opinión o expectativa, y Q es el vector de opiniones sobre los retornos:
Los puntos de vista de los inversionistas se pueden expresar como:
Donde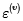 
es una inferencia no observable, normalmente distribuida con un vector aleatorio igual a cero y una matriz de covarianza diagonal 
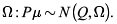La matriz Ω representa la matriz de la confianza en las opiniones o expectativas, y dependen de la matriz de covarianza inicial Σ, el parámetro de incertidumbre τ y la matriz P:
Se supone, además, que tant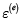o 
como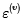 
son independientes.
Los puntos de vista del inversionista expresados con las matrices anteriores se combinan con el portafolio inicial, o de equilibrio (obtenidos mediante el modelo CAPM, definición inicial del portafolio o un modelo de Markowitz). Considerando lo anterior, los rendimientos esperados del modelo Black–Litterman se distribuyen como una normal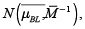 
donde la media 
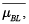está dada por:
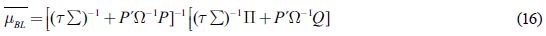
Y la matriz de covarianza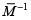 
es dada por:
A partir de la creación de un portafolio inicial de mercado y mediante el modelo de BL que se acaba de describir es posible construir un portafolio óptimo que considere las visiones y expectativas que se tienen sobre el desempeño futuro de los activos que lo conformarían; la selección de los pesos posteriores del portafolio se obtienen como:
Una vez se definen los pesos relativos de cada una de los activos se obtiene la asignación óptima de recursos, de acuerdo con las expectativas del inversionista, determinando así el portafolio óptimo de acuerdo con el modelo BL.
Finalmente, como supuestos subyacentes en la aplicación del modelo BL y al igual que en todos los modelos de teoría de portafolios analizados, se ignora el efecto de los impuestos y costos de transacción. Se supone que el mercado es eficiente y que los precios reflejan toda la información disponible en cada momento y se ajustan rápidamente a todas las variables que podrían afectar el valor de los activos; además de considerar que los inversionistas son racionales y no existe la posibilidad de realizar arbitraje.
3 APLICACIÓN DEL MODELO DE SELECCIÓN DE PORTAFOLIOS DE BLACK–LITTERMAN PARA ACTIVOS DEL MERCADO COLOMBIANO
A continuación se presenta una aplicación del modelo BL para conformar un portafolio óptimo utilizando los activos que conforman el índice COLCAP de la Bolsa de Valores de Colombia. El COLCAP refleja las variaciones de los precios de las 20 acciones más liquidas de la Bolsa de Valores de Colombia (BVC). En la aplicación se seguirán los siguientes pasos:
1. Identificación de un portafolio inicial de acuerdo con la composición del índice COLCAP.
2. Estimación de los retornos y pesos posteriores del portafolio del índice con base en las expectativas de los inversionistas, estas reflejadas en las matrices y .
3. Estimación de un portafolio óptimo de mínima varianza y un portafolio óptimo de máxima varianza, ambos mediante el modelo de Markowitz y utilizando los retornos posteriores del modelo BL.
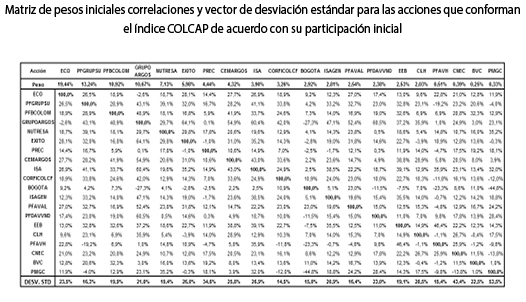
Como primer paso se identifica la estructura del portafolio inicial, que se determina asumiendo los ponderadores y participaciones iniciales de cada uno de los activos que conforman el índice COLCAP, el cual se analiza con base en datos históricos desde el 2 de enero de 2013 hasta el 30 de agosto de 2013. Las acciones, los ponderadores y la participación inicial se presentan en la tabla 2.
Una vez se identifica la estructura de portafolio del índice COLCAP se procede a optimizarlo mediante el modelo BL (paso 2) con base en las expectativas sobre algunos de los activos que lo conforman. En el COLCAP el peso de cada acción se obtiene como el cociente entre el ponderador de cada acción multiplicado por su precio en el periodo t y dividiendo por la sumatoria de los productos entre los ponderadores y los precios de cada acción en el mismo período. Con la información de rendimientos histórico de las acciones del COLCAP se construirán el vector de rendimientos iniciales y las matrices de correlación y de covarianzas necesarios para aplicar el modelo BL (ecuaciones (16 – 18)). Una vez obtenidos los pesos y rendimientos posteriores a partir del modelo BL, se utilizarán estos resultados para estructurar un portafolio eficiente mediante la propuesta de Markowitz, el cual considerará las expectativas incorporadas dentro del modelo BL (paso 3).
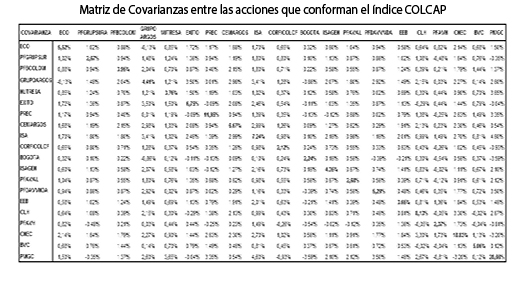
De acuerdo con los pesos iniciales de los activos que conforman el portafolio del índice, se obtienen la matriz de correlaciones iniciales, el vector de desviaciones estándar iniciales y la matriz de covarianzas iniciales, las cuales se presentan en el Anexo A.
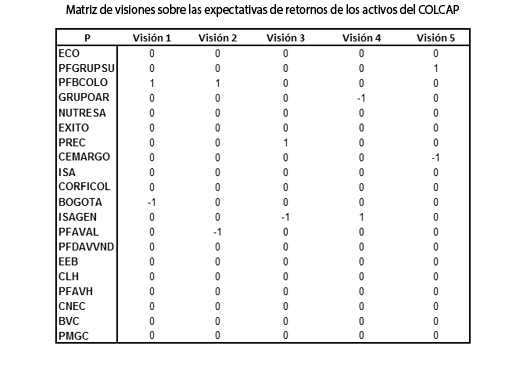
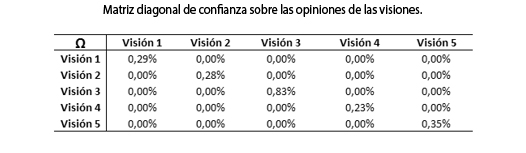
Una vez obtenidas las matrices anteriores, es posible desarrollar la propuesta metodológica del modelo BL. Para determinar el coeficiente δ se asume como rendimiento esperado libre de riesgo la DTF, expresada en términos nominales diarios. La asignación de expectativas sobre cada uno de los activos se hace en términos de la expectativa de que un activo supere el retorno de otro activo referencia (las cuales se expresan en la matriz P). Dichas visiones consideran las opiniones presentadas en la matriz Q, que para este caso precisa definir cinco visiones y cinco opiniones de excesos de retorno. Por ejemplo, en las matrices P y Q se observa que en la visión 1 (matriz P) se tiene la expectativa que la especie Preferencial Bancolombia (PFBCOLOM) supere a Banco de Bogotá (BOGOTÁ), con un exceso de retorno de 2 %. Con base en la matrices de visiones P y la matriz de covarianzas iniciales se estima la matriz de confianza en las opiniones (Ω), la cual se presenta junto con las matrices P y Q en el Anexo A.
Utilizando las ecuaciones (16) y (17), las matrices iniciales del modelo BL y asumiendo un coeficiente de incertidumbre sobre el portafolio inicial τ = 0,05, se estiman los retornos esperados del modelo de BL, junto con las correspondientes desviaciones estándar y correlaciones futuras esperadas. Los retornos esperados del modelo BL y los pesos posteriores se presentan en la tabla 3, los cuales modifican las participaciones iniciales que se presentan en la tabla 2.
Dado que el modelo BL supone que el mercado está permanentemente en un estado de equilibrio puntual, donde la oferta de activos es equiparada con la demanda por los mismos, el equilibrio instantáneo puede interpretarse como el ''centro de gravedad'', sobre el cual los mercados se desvían en todo instante, según la información que surja, pero el sistema y la información en él presionarán los precios permitiendo que el mercado vuelva a equilibrarse. La idea de equilibrio es básica para el modelo, y se entiende como un estado ideal, el cual puede ser optimizado de manera razonable mediante la estructuración de portafolios óptimos. Dados los resultados del modelo BL donde se observan desequilibrios puntuales por la dinámica de la información reflejada en las visiones de los inversionistas, se plantea como solución alternativa la estimación de los retornos y los pesos relativos mediante el uso del modelo de Markowitz, pero usando como insumo de partida el vector de retornos esperados posteriores obtenidos del modelo BL.
Al estructurar un portafolio óptimo mediante el modelo de Markowitz pero utilizando los retornos esperados y pesos posteriores del modelo BL las decisiones de inversión incorporan las expectativas de los inversionistas, las cuales, priorizando la selección de los activos sobre los que se hicieron, tienen expectativas favorables. Para los activos sobre los cuales no existen expectativas, el modelo entrega como rentabilidades esperadas las correspondientes al estado de equilibrio (portafolio inicial). Para el caso concreto se tienen expectativas sobre las acciones de PFGRUPSURA, PFCOLOMB, GRUPOARGOS, PREC, CEMARGOS, BOGOTA, ISAGEN Y PFAVAL (Ver matriz en el ANEXO A); por ejemplo, para PFGRUPOSURA, se tienen expectativas positivas y, según los resultados, se deduce que es necesario comprar acciones de esta empresa, siendo la proporción sobre el portafolio la determinada por el modelo. CEMARGOS, por el contrario, tiene perspectivas desfavorables, y la decisión debe ser no adquirir acciones de este título, en razón a que en el modelo BL su peso relativo es negativo, lo que indica que dentro del portafolio deben evitarse estos activos.
Al aplicar el modelo de Markoqitz como complemento y partiendo de los resultados del modelo BL se obtienen resultados consistentes en términos de equilibrio del portafolio y donde los pesos relativos de los activos que lo conforman, sumen el 100 %.
Partiendo de los retornos y pesos posteriores del modelo BL y aplicando el modelo de Markowitz (ecuaciones 1 – 4) se estructuran dos opciones: una donde se busca minimizar la varianza del portafolio y otra donde se busca maximizar el retorno del portafolio. Los resultados del portafolio optimizado en mínima varianza utilizando el modelo de Markowitz con insumos en los resultados del modelo BL se presentan en la tabla 4.
Como se observa en la tabla 4, la rentabilidad esperada del portafolio es de 1.2 %, mientras que la desviación estándar es de 6.1 %. Además, se puede observar que los pesos posteriores o pesos relativos de las acciones dentro del portafolio estimado por este modelo ya suman en su totalidad el 100 %. Los resultados indican que el portafolio debería estar conformado únicamente por 8 acciones de las 20 que conforman el índice. Es importante mencionar que al optimizar el portafolio que minimiza la desviación de los resultados con la restricción de las rentabilidades esperadas del modelo BL, los resultados obtenidos reconocen estas expectativas incorporadas implícitamente.
Los resultados del modelo de optimización de portafolio que busca maximizar el retorno esperado, partiendo de los resultados que incorporan las expectativas del modelo BL, se presentan en la tabla 5. Para el portafolio de máximo retorno esperado los resultados muestran que se mejora el retorno esperado, al pasar a un 1,76 %, pero se asume un mayor riesgo de portafolio, reflejado en una mayor desviación estándar del portafolio, que es igual a 6.96 %. En el caso de maximizar el retorno, se identifica que la selección óptima incluye, dentro del portafolio, 11 de los veinte activos del índice COLCAP.
Para el caso de máximo retorno se observa que se incluyen los mismos ocho activos seleccionados en el caso de mínima varianza, excepto la acción de GRUPOARGOS, sobre la cual se emitieron juicios desfavorables, pero que, en virtud de su relación retorno posterior–varianza, se incluye en el portafolio óptimo de mínima varianza.
Finalmente es importante señalar que los resultados obtenidos, tanto en el modelo inicial BL como en los modelos óptimos en varianza y retorno por medio de la teoría de Markowitz, están sujetos a la subjetividad e información del inversionista, en este caso los autores del trabajo. Sin embargo, estos resultados son óptimos desde el desarrollo de la metodología propuesta.
4 CONCLUSIONES
En este trabajo se presenta una revisión teórica de las principales propuestas de análisis y estructuración de portafolios en la teoría financiera. Además, se profundiza en los aspectos teóricos del modelo Black–Litterman y se hace una aplicación para estructurar un portafolio óptimo que incluya visiones y expectativas de los autores con relación a algunos activos del índice COLCAP del mercado colombiano.
En la aplicación del modelo se muestra cómo la propuesta de BL sirve para estimar los retornos esperados de acuerdo con las visiones y expectativas de los inversionistas y cómo los resultados de este modelo son un insumo para realizar una mejor optimización de la destinación de los recursos en un portafolio estructurado mediante el modelo de portafolio de Markowitz que para este caso se analizó desde dos perspectivas: mínima varianza y máximo retorno.
Al analizar el modelo de BL, obtener las rentabilidades esperadas y utilizarlas como insumo del modelo de Markowitz, se obtienen resultados más consistentes en la medida en que incluyen implícitamente las expectativas de los inversionistas, las cuales se reflejan en el vector de retornos posteriores del modelo BL. La consistencia de los resultados también se puede observar en la asignación coherente del 100 % de los recursos, lo cual no siempre es posible con el modelo BL, en el cual los pesos posteriores son indicativos y en términos de preferencias principalmente.
Finalmente, la aplicación conjunta de los modelos Black–Litterman y Markowitz representa una metodología para aquellos inversionistas que buscan obtener un mejor rendimiento de su portafolio de inversión y que, además, disponen de información que les permita formarse unas expectativas sobre algunos títulos particulares del índice (o de cualquier referencia para la creación de portafolio inicial).
Es importante señalar que aunque estos modelos permiten obtener combinaciones óptimas en términos de rendimiento y mínimo riesgo, el modelo no considera los posibles riesgos que puedan afectar los retornos esperados como lo son el riesgo cambiario, el riesgo político, el riesgo crédito y el riesgo liquidez, que para este caso particular pueden afectar al índice en el mercado bursátil.
REFERENCIAS
[1] H. Markowitz, ''Portafolio selection,'' Journal Of Finance vol. 7, p. 91, 1952.
[2] F. Black, y R. Litterman. ''Global portfolio optimization''. Financial Analysts Journal, 48(5), p. 16. 1992
[3] A. M. Zubeldia, L. M. M. Zabalza, y M. Z. Zubiaurre, ''El modelo de Markowitz en la gestión de carteras,'' Cuadernos de Gestión vol. 2, p. 45, 2002.
[4] J. Tobin, ''Liquidity preference as behavior towards risk'' The Review of Economic Studies''. Vol. 25. p.65. 1958.
[5] W. F. Sharpe, ''Capital asset prices: a theory of market equilibrium under conditions of risk,'' The Journal of Finance, vol. 19, p. 442, 1964.
[6] S. Ross. ''The arbitrage theory of capital asset pricing'' Journal of Economic Theory. vol. 13, p. 341, 1976.
[7] P. Artzner, F. Delbaen, J.–M. Eber, y D. Heath, ''Coherent measures of risk,'' ETH Zürich, Working Paper, 1998.
[8] W.–G. Zhang, W.–L. Xiao, y Y.–L. Wang, ''A fuzzy portafolio selection method based on possibilistic mean and variance,'' Soft Cutiomp, vol. 33, p. 633, 2008.
[9] G. Buenaventura y A. Cuevas, ''Una propuesta metodológica para la optimización de portafolios de inversión y su aplicación al caso colombiano,'' Estudios Gerenciales, vol. 95, p. 24, 2005.
[10] R. Becerra y L. Melo, ''Medidas de riesgo financiero usando cupulas: teoría y aplicaciones,'' Borradores de economía, vol. 489, 2008.
[11] P. Castillo y R. Lama, ''Evaluación de portafolio de inversionistas institucionales: fondos mutuos y fondos de pensiones,'' Revista Estudios Económicos, Banco Central de Reserva del Perú, vol 3. p. 1, 1998.
[12] E. Cruz, J. Urrutia, y P. Medina, ''Un modelo dual para portafolios de inversion,'' Scientia Et Technica, vol. 17, p. 118, 2011.
[13] R. Cruz, y A. Clement, ''Aplicación del Modelo de Black – Litterman a laSelección de Portafolios Internacionales,'' Ciencias de la administración, UNAM, México, 2012.
[14] A. Puerta y H. Laniado, ''Diseño de estrategias óptimas para la selección de portafolios, un análisis de la ponderación inversa al riesgo,'' Red de Revistas Científicas de América Latina, Lecturas de Economía, p. 273, 2010.
