ARTÍCULOS

Un algoritmo basado en búsqueda tabú granular para la solución de un problema de ruteo de vehículos considerando flota heterogénea¹

An algorithm based on a granular tabu search for the solution of a vehicle routing problem by considering heterogeneous fleet

Duván Eduardo Puenayán^*; Julio César Londoño^**; John Willmer Escobar^***; Rodrigo Linfati^****

* Asistente de Investigación. Ingeniero industrial, Escuela de Ingeniería Industrial Universidad del Valle. Email: duvanedu87@hotmail.com.

** Profesor Tiempo Completo. Magíster en Ingeniería Industrial, Universidad del Valle. Escuela de Ingeniería Industrial Universidad del Valle. Email: julio.londono@correounivalle.edu.co.

*** Corresponding Author. Profesor tiempo completo, Pontificia Universidad Javeriana Cali, Colombia. PhD in Operations Research, University of Bologna, Italy. Magíster en Ingeniería Industrial, Universidad del Valle, Cali, Colombia. Especialista en Finanzas, Universidad del Valle, Cali, Colombia. Ingenierio Industrial, Universidad del Valle, Cali, Colombia. Departamento de Ingeniería Civil e Industrial, Pontificia Universidad Javeriana, Calle 18 N.° 118-250, Cali, Colombia. Email: johnwillmer.escobar2@unibo.it. Tel: +572 3218200 ext. 8016.

**** Profesor Tiempo Completo, Universidad del Bío-Bío, Chile. PhD in Operations Research, University of Bologna, Italy. Magíster en Ingeniería Industrial, Universidad de Concepcion, Concepcion, Chile. Ingeniero Civil Industrial, Universidad de Concepcion, Concepcion, Chile. Email: rlinfati@ubiobio.cl;

Recibido: 15/05/2014
Aceptado: 27/06/2014

RESUMEN

Este artículo aborda el problema de ruteo de vehículos con flota heterogénea (VRPH), en el cual se busca determinar las rutas a ser construidas para satisfacer las demandas de los clientes, considerando una flota de vehículos con capacidad y costos no homogéneos. El objetivo es minimizar la distancia total de las rutas recorridas por los diferentes vehículos. En este artículo, se propone un algoritmo metaheurístico basado en una búsqueda tabú granular para la solución del problema. El algoritmo acepta soluciones infactibles penalizadas por un factor dinámico que se ajusta durante la búsqueda. Experimentos computacionales en instancias reales de una compañía colombiana muestran que el algoritmo propuesto es capaz de obtener, en tiempos computacionales reducidos, mejores soluciones que las obtenidas por el método tradicional de planificación de rutas, usado en la compañía.

PALABRAS CLAVE

problema de ruteo de vehículos, flota heterogénea, búsqueda tabú granular

ABSTRACT

This paper considers the vehicle routing problem with heterogeneous fleet (VRPH), which tries to determine the routes to be constructed for satisfying the demand of the customers by considering a fleet of vehicles with different capacities and costs not homogeneous. The main objective is to minimize the distance traversed by the different vehicles. This paper proposes a metaheuristic algorithm based on a granular tabu search for the solution of the problem. The algorithm allows infeasible solutions by penalizing them by a dynamic factor which is adjusted during the search. Computational experiments on real instances for a Colombian company show that the proposed algorithm is able to obtain, within short computing times, better solutions for those obtained by the current traditional method for planning the routes.

KEY WORDS

vehicle routing problem, heterogeneous fleet, granular tabu search

INTRODUCCIÓN

Debido a los cambios causados por la globalización, y al acceso a nuevos mercados, culturas y tecnologías, las empresas se ven obligadas a tomar cada vez decisiones más complejas tratando de lograr un alto grado de competitividad. Un factor esencial para la competitividad de las compañías es la administración de la logística y su relación con el nivel de servicio al cliente. Dentro de este aspecto, una de las decisiones de mayor transcendencia que las compañías deben afrontar está relacionada con el diseño y gestión de la distribución física, que consisten en todas aquellas actividades encaminadas a la planificación, implementación y control de un flujo de productos finales desde el punto de distribución (CD) hasta los clientes finales. En este contexto la programación y el diseño de rutas en los sistemas de transporte son fundamentales para su buen funcionamiento. Centrándose en la dificultad de la distribución física se puede establecer que el problema de entregar productos desde ciertos depósitos a sus usuarios finales (ruteo de vehículos-VRP) desempeña un papel central en la gestión de algunos sistemas logísticos, y su adecuada planificación puede significar considerables ahorros [1].

El presente artículo está enfocado en el desarrollo de un algoritmo metaheurístico basado en una búsqueda tabú granular para la solución de la problemática de ruteo de vehículos considerando flota heterogénea (VRPH). En particular, se busca determinar el mejor diseño y programación de rutas de vehículos con el fin de disminuir los costos incurridos en los sistemas de transporte, considerando una flota de vehículos con diferentes capacidades y costos asociados. Más específicamente, se debe asignar el tipo de vehículo que atenderá a un conjunto de clientes y la ruta a seguir para satisfacer sus demandas. El VRPH es un problema NP-hard debido a que es una generalización del problema de ruteo de vehículos con restricciones de capacidad (CVRP), donde los vehículos pueden tener capacidades y costos diferentes. El estudio del VRPH es de gran interés para la comunidad científica debido a que permite resolver muchos casos reales para diferentes compañías.

El algoritmo propuesto ha sido probado en un caso real de una compañía colombiana de productos de consumo masivo que realiza despachos en las principales zonas urbanas de la ciudad de Cali (Colombia). En el planteamiento de este problema, los siguientes supuestos han sido considerados: i) los pedidos de los clientes serán entregados completos, es decir, que no se permiten entregas divididas, ii) los clientes no tienen horarios de atención específicos, es decir, que no se consideran ventanas de tiempo, iii) la compañía caso de estudio cuenta con ocho vehículos para el transporte de la mercancía, iv) la flota de camiones es heterogénea y está disponible completamente en el centro de distribución (CD).

Una revisión del estado del arte para el problema de VRPH es descrita en la sección 1. La sección 2 detalla el algoritmo propuesto. Los resultados computacionales son presentados en la sección 3. Finalmente, conclusiones e investigación futura se detallan en la sección 4.

1. REVISIÓN DE LA LITERATURA

De acuerdo con Cordeau et al. [2], el problema de ruteo de vehículos con flota heterogénea puede ser descrito de la siguiente manera: dada una flota de vehículos con capacidad no homogénea, un depósito común y un conjunto de clientes, se debe encontrar el conjunto de rutas que han de ser desarrolladas y que minimice la distancia total recorrida. En el VRPH, se debe determinar la ruta y el tipo de vehículo a usar con el fin de atender a un conjunto de clientes, sin sobrepasar la capacidad de cada vehículo [3].

Aunque en la teoría del problema de ruteo de vehículos (VRP) a menudo se supone que la flota de vehículos es homogénea, en situaciones reales los vehículos difieren en sus equipos, capacidad de carga, edad y estructura de costos [4]. De acuerdo con la clasificación propuesta por Farahani et al. [5], existen tres tipologias del problema de VRPH:

• Problema de ruteo de vehículos heterogéneo con flota combinada (VRPHCF): inicialmente introducido por Golden et al. [6]. El VRPHCF considera el mismo valor para los costos variables, independientemente del tipo de vehículo que realiza cada ruta. Se considera un número ilimitado de vehículos de cada tipo.

• Problema de ruteo de vehículos heterogéneo con flota variable (VRPHFV): Considera diferentes costos variables que dependen del tipo de vehículo. Al igual que el VRPHCF, también se considera un número ilimitado de vehículos de cada tipo. Para mayores detalles se recomienda revisar Osman y Salhi [7].

• Problema de ruteo de vehículos heterogéneo restringido (VRPHR): Se considera restricciones en el número de vehículos disponibles para cada tipo. Para mayores detalles se puede revisar Baldacci et al. [8].

Algoritmos exactos para el VRPH pueden ser consultados en [5]. Una revisión de la literatura relacionada con el VRPH ha sido propuesta por [8]; en su trabajo muestran que algoritmos heurísticos y metaheurísticos propuestos han sido adaptaciones o extensiones de los métodos propuestos en las últimas décadas para las variantes básicas del VRP.

En [6] se propone un algoritmo para el VRPH basado en el método de los ahorros. En particular, se extiende el concepto de ahorro en un par de clientes incluyendo los costos fijos del vehículo. Una variante del algoritmo de los ahorros para el VRPH, denominada ROS-γ, es propuesta por Renaud y Boctor [9]. Dicho algoritmo utiliza cinco procedimientos de búsqueda local subordinados (Orden, 1-pétalo, 2 pétalos, Selección de Pétalos y Mejora).

Desrochers y Verhoog [10] proponen un algoritmo de ahorros basado en Matching (MBSA) para el VRPH. Dicho algoritmo se basa en la fusión de rutas sucesivas mediante la resolución de un problema de Matching.

En Gheysens et al. [11-12] se presentan dos heurísticas para el VRPH. En el primer trabajo, se incorpora la restricción de capacidad del vehículo en la función objetivo, junto con los costos fijos de los vehículos y los costos variables de la ruta, mediante el uso de multiplicadores de penalización. El problema resultante se resuelve usando el algoritmo MGT + Or-Opt para diferentes valores de multiplicadores de penalización. En el segundo trabajo, se usa un algoritmo de dos etapas; en la primera etapa, la mezcla de vehículos utilizados se calcula mediante una cota inferior, y en la segunda etapa, un procedimiento de asignación generalizada (GAP) propuesto se utiliza para resolver el problema de ruteo resultante.

Un algoritmo metaheurístico basado en recocido simulado (RS) para el VRPH con ventanas de tiempo ha sido propuesto por Bräysy et al. [13]. La metaheurística se basa en tres fases: i) generación de una solución inicial por medio de una heurística basada en ahorros, combinando estrategias de diversificación con mecanismos de aprendizaje, ii) reducción del número de rutas mediante un procedimiento de búsqueda local y iii) aplicación de cuatro operadores de búsqueda local para guiar el proceso de mejora.

Algoritmos de búsqueda tabú para resolver el VRPH han sido propuestos en [7], Gendreau et al. [14] y Wassan y Osman [15]. En [7] se obtiene una solución inicial por medio de un algoritmo heurístico simple y el mejoramiento propuesto en Osman [16].

Para el mejoramiento se emplea un mecanismo de generación de vecindarios, evaluando el costo de un movimiento, una estructura de datos para la lista de candidatos, y un criterio de aspiración.

En [14] se hace uso de la heurística GENIUS. En particular se usa un procedimiento de memoria adaptativo (AMP) con una técnica eficiente de diversificación e intensificación probabilística. Finalmente, en [15], se combinan varias estrategias eficaces para mejorar la calidad global de la solución. El algoritmo incluye: (i) una solución inicial S y (ii) un vecindario para generar conjunto de soluciones N(S).

2. MATERIALES Y MÉTODOS

2.1 Búsqueda granular

El algoritmo propuesto está basado en la idea de búsqueda granular introducida por Toth y Vigo [17]. Para reducir considerablemente el tiempo de cálculo requerido en la exploración de vecindades, en [17] se ha propuesto el uso de espacios de búsqueda ''granular'' para el problema de ruteo de vehículos con restricciones de capacidad. La idea de la búsqueda granular está basada en el uso de una lista de ''buenas soluciones vecinas'', llamada Lista de Candidatos. El espacio de búsqueda granular, determinado por la Lista de Candidatos, es obtenido por la unión de los arcos ''cortos'', los arcos incidentes a los depósitos y los arcos que pertenecen a las mejores soluciones encontrados durante la búsqueda [18]. De acuerdo con [17], la lista de candidatos se obtiene eliminando soluciones vecinas que no son susceptibles de pertenecer a soluciones factibles de alta calidad. De esta manera se conduce a la realización de búsquedas, en las cuales solo movimientos potencialmente ''prometedores'' son evaluados en cada iteración.

Aplicaciones exitosas de la metodología de búsqueda granular para solucionar problemas de ruteo de vehiculos junto con decisiones de localización pueden ser consultadas en [18-20].

2.2 Solución inicial

La solución inicial S está basada en la idea de barrido propuesta en [9]. De esta manera se obtiene una solución en un tiempo computacional reducido. El algoritmo 1 muestra en detalle la descripción de la solución inicial.

Algoritmo 1

Entrada: Matriz de distancias reales

Salida: Rutas Iniciales

INICIO

Calcular ángulos de los clientes y ordenar de manera no decreciente

Ordenar los camiones de acuerdo con su capacidad de manera no ascendente

Seleccionar primer vehículo

Mientras exista demanda no satisfecha, hacer

Si CapActual + DemandaClienteCapCamion entonces

Asignar cliente al vehículo

CapActual = CapActual+DemandaCliente

Actualizar CapActual y longitud de la ruta actual

Marcar demanda como satisfecha

Si NO

Seleccionar siguiente vehículo

Fin SI

Fin Mientras

Secuenciar rutas iniciales usando VMC

FIN

La secuenciación de las rutas se hizo mediante el algoritmo del vecino más cercano (VMC). Note que el algoritmo considera cada cliente como ''inicial'' para realizar el método del barrido. En otras palabras, se evalúan n configuraciones, donde n es el número de clientes. El algoritmo encuentra la mejor solución inicial S₀, aunque el número de rutas exceda la cantidad de vehículos disponibles. El número de rutas será mejorado mediante la búsqueda tabú granular.

2.3 Algoritmo de búsqueda tabú granular (BTG)

El algoritmo 2 muestra en detalle la búsqueda tabú granular.

Algoritmo 2

Entrada: Solución inicial S₀

Parámetros de la BTG

Salida: Mejor solución encontrada S^*

INICIO

Hacer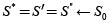

Crear lista tabú

Crear lista de candidatos

Mientras no se cumpla el criterio de parada, Hacer

Por cada vecino Sⁿ en los vecindarios de S', Hacer

Si NO es candidato, entonces ir al siguiente vecino

Si es tabú, entonces ir al siguiente vecino, excepto si cumple criterio de aspiración

Si Sⁿ es factible y 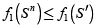, entonces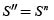

Si Sⁿ es infactible y 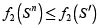, entonces S'' = Sⁿ

Fin por cada

Aceptar el movimiento haciendo S' = S''

Actualizar lista de candidatos

Actualizar lista tabú incorporando a la lista el movimiento que generó S'

Actualizar penalidades

Si S' es factible y f₁(S') < f₁(S^*), entonces S^* = S'

FIN

Como se menciona anteriormente, el algoritmo usa una estrategia de lista de candidatos, con el fin de reducir el número de movimientos poco prometedores. Los mejores movimientos seleccionados por la distancia más corta dependen de un parámetro de dispersión llamado β [17]. Los arcos ''cortos'' se han determinado con base en el umbral de granularidad ν calculado en la ecuación (1). En particular, un arco es clasificado como ''corto'', si la distancia es menor a ν:

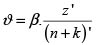
Donde β es un parámetro de dispersión positivo, z' es el valor objetivo de la solución inicial f₁(S₀) y (n + k)' es el número de clientes (n) más las rutas obtenidas (k) en dicha solución. Inicialmente el factor de esparsificación β es ajustado a un valor pequeño #946;₀. Cuando la mejor solución factible no es mejorada después de N_beta iteraciones, el factor de esparsificación β es incrementado a β_b. Luego un nuevo grafo es calculado, y N_change iteraciones son desarrollados comenzando de la mejor solución factible encontrada. Finalmente, el factor de esparsificación toma nuevamente su valor original β₀. La búsqueda continua β₀, β_d, N_beta y N_change, son parámetros dados.

El algoritmo propuesto permite soluciones infactibles con respecto a las capacidades de los vehículos. Dada una solución factible S durante la búsqueda tabú granular, se asigna un valor de la función objetivo f₁(S). El valor de f₁(S) es igual a distancia recorrida por los arcos que pertenecen a las rutas de la solución S. En adición, para cada solución no factible con respecto a la capacidad del vehículo, se adiciona a f₁(S) un término de penalización obtenido por la multiplicación de la capacidad extra del vehículo por un parámetro de penalización dinámicamente actualizado durante la búsqueda ∝_r. De esta manera, el valor de la función objetivo f₂(S) es obtenido. Note que si la solución S es factible f₂(S) = f₁(S).

En particular, si se han encontrado soluciones infactibles respecto a la capacidad del vehículo durante N_fact iteraciones, el valor del factor de penalización ∝_r es calculado como el min{α_max, ∝_r × δ_inc}, donde δ_inc 1. De lo contrario, si soluciones factibles se han encontrado con respecto a la capacidad del depósito durante N_fact iteraciones, el valor del factor de penalización ∝_r es calculado como max{β_min, ∝_r × δ;_red}, donde δ_red < 1. N_fact, ∝_r, α_max, α_min, δ_inc y δ_red son parámetros. El algoritmo propuesto aplica movimientos entre rutas y al interior de las rutas correspondiente al vecindario de inserción. En la inserción, un cliente es transferido de su posición actual a otra posición, dentro de la misma ruta o en una ruta diferente. La figura 1 muestra un ejemplo del movimiento de inserción entre la ruta 1 y 2.

Una vez elegida la nueva solución S, se procede a guardar los arcos nuevos en la lista de candidatos y lista tabú. Posteriormente dichos arcos son considerados tabú por t_iter iteraciones. Donde T_iter es un parámetro. El siguiente criterio de aspiración es aplicado: si el valor de la función objetivo f₂(S) de la nueva solución S es menor que el costo de la mejor solución encontrada durante la búsqueda, el movimiento que produce a S es ejecutado inclusive si este corresponde a un movimiento tabú. El procedimiento BTG se realiza hasta que se cumpla el criterio de parada, equivalente a N_iter.

Otros puntos importantes sobre el algoritmo propuesto son las estrategias de diversificación e intensificación. El algoritmo itera entre etapas largas de intensificación y etapas cortas de diversificación, relacionadas con los valores del parámetro de dispersión β durante la búsqueda. Valores grandes de β inducen procesos de diversificación, mientras que valores pequeños de β permiten procesos de intensificación.

3. RESULTADOS COMPUTACIONALES

El algoritmo propuesto ha sido implementado en lenguaje C⁺⁺ bajo Linux Ubuntu 13.10. Las pruebas computacionales han sido ejecutadas en un computador Hp Pavilion dv4-2025 con procesador Intel Core i3 (2.13 GHz) con 4 GB de memoria RAM y disco duro de 500 GB.

La compañía caso de estudio considera la distribución diaria de aproximadamente 79 clientes, cuyas coordenadas geográficas se conocen con exactitud. La compañía caso de estudio cuenta con ocho vehículos para el transporte de la mercancía, los cuales pueden transitar una máxima velocidad de 45 km/h. La flota de camiones está compuesta por 1 camión de 18 toneladas, 1 camión de 15 toneladas, 4 camiones de 12 toneladas y 2 camiones de 8 toneladas. El centro de distribución (CD) se encuentra ubicado en la coordenada (0,0).

3.1 Parametrización

El éxito del algoritmo propuesto depende directamente de los parámetros utilizados; es por ello que se han realizado pruebas computacionales extensas para lograr establecer los mejores valores para resolver la instancia consideradas en esta investigación. La tabla 1 muestra los valores obtenidos para los parámetros.

Los parámetros β₀ y β_d permiten al algoritmo alternar entre fases de intensificación y diversificación, respectivamente. El proceso de intensificación se realiza durante N_change iteraciones, mientras que el proceso de diversificación se realiza durante N_beta iteraciones. Los parámetros N_fact, ∝_r, α_max, α_min, δ_inc y δ_red están relacionados con el esquema de penalización, el cual permite considerar soluciones infactibles respecto a la capacidad del vehículo durante la búsqueda. El proceso para la sintonización final de parámetros se ha realizado de acuerdo con el procedimiento propuesto en Coy et al. [21].

3.2 Resultados obtenidos

La tabla 2 muestra los resultados obtenidos por el procedimiento de solución inicial. La columna 1 muestra el número de la ruta (ruta); la columna 2 muestra la capacidad del vehículo asignado para la ruta (camión); la columna 3 muestra la distancia recorrida en metros (distancia ruta) y las columnas 4 y 5 muestran la demanda atendida en la ruta en kilogramos y el porcentaje de utilización del vehículo respecto a su capacidad, respectivamente.

Como se puede apreciar en la tabla 2 , el número de rutas creadas por el método de la solución inicial excede la cantidad de vehículos disponibles en el caso de estudio (se crean 9 rutas con 8 vehículos disponibles). La distancia total recorrida fue de 227 584 m, el promedio de utilización en cuanto a capacidad de los vehículos fue del 83.26 % y el tiempo computacional es de 0,01 segundos. En la figura 2 se muestran las rutas generadas por el procedimiento de solución inicial.

Como se puede apreciar en la figura 2 , algunas de las rutas iniciales presentan cruces, lo cual podría considerarse ineficiente en el diseño de rutas. Como se mencionó anteriormente, la solución inicial puede ser no factible respecto al número de vehículos utilizados; sin embargo, la búsqueda tabú granular permite eliminar las rutas menos cargadas.

En la tabla 3 se muestran los valores obtenidos como solución final. El algoritmo propuesto empleando únicamente los vehículos que se tenían disponibles para el caso estudio (8 rutas son desarrolladas). La distancia total recorrida es de 170 986 m, el promedio de utilización en cuanto a capacidad de los vehículos fue del 92.82 % y el tiempo computacional es de 33,10 segundos. En general existe un ahorro de distancia de 24.86 % respecto a la solución encontrada por el procedimiento inicial.

La solución final obtenida presenta un valor promedio de utilización mejor de la capacidad de los vehículos. La solución final obtenida logra una disminución de distancia y tiempo de viaje. En la figura 3 se muestran las rutas finales generadas por el algoritmo propuesto.

3.3 Análisis de sensibilidad sobre la solución Inicial

Una manera de comprobar el desempeño del algoritmo propuesto es modificando la solución inicial. De manera opcional se ha implementado el algoritmo de los ahorros. Este método proporcionó una mejor solución inicial que la obtenida por el método del barrido. La tabla 4 muestra los resultados obtenidos por el algoritmo de los ahorros.

Como se aprecia en la tabla 4 , el número de rutas creadas por el método de ahorros es 9, similar al procedimiento inicial propuesto. El tiempo computacional obtenido es de 0,08 segundos. La distancia total recorrida obtenida es de 182 606 m, esto es, 44 978 m menos que la distancia obtenida por el procedimiento inicial propuesto. De igual manera, el promedio de utilización de la capacidad de los vehículos es mayor. La figura 4 muestra las rutas creadas por la solución inicial obtenida por el método de los ahorros.

Manteniendo los parámetros constantes descritos en la sección 3.1, se obtuvieron los resultados presentados en la tabla 5.

La distancia total recorrida fue de 173 953 m; el promedio de utilización de los vehículos es del 91.67 % y el tiempo computacional para obtener la respuesta fue de 10,06 segundos. La figura 5 muestra las rutas creadas por la solución final considerando el método inicial por el algoritmo de los ahorros.

En la tabla 6 se muestra la comparación de los valores obtenidos por el algoritmo propuesto considerando la solución inicial propuesta y la solución inicial obtenida por el método de los ahorros.

Note que la mejora de la distancia tiene un valor más significativo con el método inicial propuesto que con el método inicial de los ahorros. De esta manera confirma que el algoritmo queda atrapado en un mínimo local más fácilmente con una solución inicial de mejor calidad. De esta manera, se opta por considerar la mejor solución final independientemente del tiempo computacional empleado.

4. CONCLUSIONES Y FUTURAS INVESTIGACIONES

En este artículo se propone un algoritmo efectivo basado en la metaheurística BTG para el problema ruteo de vehículos con flota heterogénea (VRPH). En particular, el algoritmo propuesto utiliza estrategias de diversificación e intensificación de manera simultánea, un esquema de penalización para aceptar soluciones infactibles y un vecindario granular.

El algoritmo propuesto ha sido evaluado considerando una instancia real de una compañía de productos de consumo masivo colombiana. Los experimentos computacionales muestran que el algoritmo propuesto es capaz de obtener, dentro de razonables tiempo de computación, soluciones de gran calidad. Como se vio en la validación del modelo, la metodología propuesta en este trabajo conlleva una mejora sustancial en relación a los costos de transporte, representado en los vehículos empleados, el porcentaje de utilización de capacidad de cada camión y la distancia total recorrida.

Los resultados obtenidos sugieren que el algoritmo propuesto podría ser aplicado a otros problemas de distribución similares. Trabajos futuros propuestos son los siguientes:

• Evaluar el algoritmo propuesto considerando funciones objetivo diferentes como la minimización de la cantidad de vehículos o la minimización de los costos fijos por el uso de vehículos.

• Considerar otra lista de candidatos teniendo en cuenta la cantidad de clientes cercanos entre sí. Para cada cliente se considera que otro es vecino si está dentro de los C clientes más cercanos sin importar la distancia que se encuentre.

Notas:

1 Artículo de investigación enmarcado en el proyecto ''Algoritmos heurísticos para problemas de ruteo con múltiples depósitos'' financiado por la Universidad del Valle y la Pontificia Universidad Javeriana Cali.

REFERENCIAS

[1] P. Toth, y D. Vigo. The Vehicle Routing Problem, Philadelphia: SIAM Monographs on Discrete Mathematics and Applications, 2000, 384 p.

[2] J. Cordeau et al. ''Vehicle Routing''. Handbook in OR &MS, 14(06), pp. 367–428, 2007.

[3] S. H.-Y., Shen, y F.-H. Liu. ''A Method for Vehicle Routing Problem with Multiple Vehicle Types and Time Windows'', presentado en Natl. Sci. Counc. ROC(A), 23(4), 526–536, 1999.

[4] W. Dullaert et al. ''New heuristics for the fleet size and mix vehicle routing problem with time windows''. Operations Research, 53, pp. 1232–1238, 2002.

[5] R. Z. Farahani et al. Logistics Operations and Management: Concepts and Models. Elsevier, Ed., 2011, 475 p.

[6] B. Golden et al. ''The fleet size and mix vehicle routing problem''. Computers & Operations Research, 11(1), pp. 49–66, 1984.

[7] I.H. Osman y S., Salhi. ''Local Search Strategies for the Vehicle Fleet Mix Problem''. Modern Heuristic Search Methods, 1, pp. 131–153, 1996.

[8] R. Baldacci, et al. Routing a Heterogeneous Fleet of Vehicles, The vehicle routing problem: latest advances and new challenges, 2007, 25 p.

[9] J. Renaud, y F.F Boctor. ''A sweep-based algorithm for the fleet size and mix vehicle routing problem''. European Journal Of Operational Research, 140, pp. 618–628, 2002.

[10] M. Desrochers y T.W. Verhoog. A new heuristic for the fleet size and mix vehicle routing problem. Computers and Operations Research, 18, pp. 263–274, 1991.

[11] F. Gheysens, et al. ''A comparison of techniques for solving the fleet size and mix vehicle routing problem''. OR Spektrum, 6, pp. 207–216, 1984.

[12] F. Gheysens et al. ''A new heuristic for determining fleet size and composition''. Mathematical Programming Study, 26, pp. 233–236, 1986.

[13] Bräysy et al. ''An effective multi-restart deterministic annealing methauristic for the fleet size and mix vehicle routing problem with time windows''. Transportation Science, 1, pp. 1–29, 2006.

[14] J. Gendreau et al. ''A tabu search heuristic for the heterogeneous fleet vehicle routing problem''. Computers & Operations Research, 26, pp. 1153–1173, 1999.

[15] N. A. Wassan, y I. H Osman. ''Tabu search variants for the mix fleet vehicle routing problem''. Journal of the Operational Research Society, 53, pp. 768–782, 2002.

[16] I. H. Osman. ''Metastrategy simulated annealing and tabu search algorithms for the vehicle routing problem''. Annals of Operations Research, 41, 421–451, pp. 1993.

[17] P. Toth, y D. Vigo, ''The granular tabu search and its application to the vehicle routing problem'', INFORMS Journal on Computing, 15(4), pp. 333–346, 2003.

[18] J. W. Escobar et al. ''Un algoritmo metaheurístico basado en recocido simulado con espacio de búsqueda granular para el problema de localización y ruteo con restricciones de capacidad''. Revista Ingenierías Universidad de Medellín, enero-junio, pp. 139-150, 2012.

[19] J. W. Escobar et al. ''A two-phase hybrid metaheuristic algorithm for the capacitated location-routing problem''. Computers & Operations Research 40 (1), pp. 70–79, 2013.

[20] J. W. Escobar et al. ''A hybrid Granular Tabu Search algorithm for the Multi-Depot Vehicle Routing Problem''. Journal of Heuristics, pp. 1–27, DOI: 10.1007/s10732-014-9247-0, 2014.

[21] S. P. Coy et al. Using experimental design to find effective parameter settings for heuristics, Journal of Heuristics, 7(1), pp. 77–97, 2001.